一种基于EEMD的时间序列数据异常值检测和校正方法与流程

本发明涉及一种基于eemd的时间序列数据异常值检测和校正方法，数据处理领域。

背景技术：

对于时间序列异常值检测方法的研究，前人已经提出了很多算法，如基于统计、聚类、距离、密度等异常值检测方法。但是这些方法没有考虑时间序列数据的时序变化特性，而是从数据全集考虑，隐藏在局部的异常值难以检测

经验模态分解(empiricalmodedecomposition，emd)方法是由nordene.huang等人于1998年提出。emd在机械故障诊断、地球物理探测、生物医学分析等方面都得到广泛的应用。尚未见有文献用于时间序列异常值检测。emd可将不同尺度的波动或趋势从原信号中逐级分离出来。emd适用于分析非线性非平稳信号，且具有完全自适应性。原始的时间序列x(t)经过emd分解得到一系列固有模态函数(intrinsicmodefunction，imf)和一个残余项(residual,简记res)，即

其中ci表示第i个imf，rn为残余项。eemd是emd的改进算法，有效解决了emd的混频现象。

曲线拟合的原理是已知样本点(xi,yi)(i＝1,2,3,…,n)，求出解析函数y≈f(x)，使f(x)在原样本点xi上尽可能接近yi的值。曲线拟合方法包括最小二乘曲线拟合(多项式拟合)和线性插值拟合，最小二乘曲线拟合，就是使误差平方和最小的多项式拟合。即寻找一条曲线使在误差平方和最小的准则下与所有数据点最为接近，也即找出使最小的f(x)。通常，多项式的次数选用3次，低于3次，可能会造成波峰丢失，高于3次，拟合时间长，容易产生虚假波峰。

技术实现要素：

本发明的技术解决问题是：克服现有技术的不足，提供了一种基于eemd的时间序列数据异常值检测和校正方法，用于解决监测数据存在不可靠数据的问题。

本发明的技术解决方案是：

一种基于eemd的时间序列数据异常值检测和校正方法，步骤如下：

(1)对原始时间序列数据，按照时间顺序进行排序，对缺失数据用0值填补，得到初步整理数据；

(2)对所述初步整理数据进行异常值检测处理，把检测出的异常值用0值替换；

(3)对异常值检测处理之后的数据进行异常值校正处理，即对数据中的0值进行填补，完成时间序列数据异常值检测和校正。

步骤(2)对初步整理数据进行异常值检测处理，包括如下步骤：

(2.1)通过中位数法对所述初步整理数据进行初步检测；

(2.2)通过eemd法对所述初步检测之后的数据进行精细检测。

所述步骤(3)对异常值检测处理之后的数据进行异常值校正处理，采用曲线拟合法实现。

所述通过中位数法对所述初步整理数据进行初步检测，具体为：

(4.1)对于初步整理后的时间序列数据{ai}，i＝1,2,3,…,，把{ai}中的正数选出来构成一个新的数列把的中位数记为

(4.2)计算中每个数与中位数的比值即

(4.3)设定的阈值为r1,r2，若或者则为异常值，把异常值替换为0，时间序列数据{ai}经过替换后得到的数列为{bi}，从而完成对所述初步整理数据进行初步检测。

所述通过eemd法对所述初步检测之后的数据进行精细检测，具体为：

(5.1)将数列{bi}中的正数选出来构成一个新的数列

(5.2)通过eemd法对进行分解，得到频率从高到低排列的n个分量；

(5.3)n个分量中，舍去高频分量，把后面m个低频分量以向量求和的方式进行求和，得到一个新的数列其中，1<m<n；

(5.4)计算偏差比率用于量化与的偏离程度；

(5.5)设定偏差比率的阈值为d0，偏差比率大于d0的数据为异常值，再把异常值替换为0，把{bi}经过异常值替换得到的数列记为{gi}，从而完成对所述初步检测之后的数据进行精细检测。

所述步骤(5.1)将数列{bi}中的正数选出来构成一个新的数列时，每个正数之间的排列顺序不变。

所述步骤(5.2)中，n个分量中包括n-1个imf和1个残余项rn。

round为四舍五入取整函数。

偏差比率

本发明与现有技术相比的有益效果是：

(1)从整体技术方案上来讲，本发明方法能够更加精确检测异常值，既不会错检，也不会漏检。

(2)与现有技术相比，本发明方法不仅能够从数据全集检测出异常值，还能从时间序列局部检测异常值。

(3)本发明方法计算容量小，计算机程序运行实现时间短。

附图说明

图1为本发明流程图；

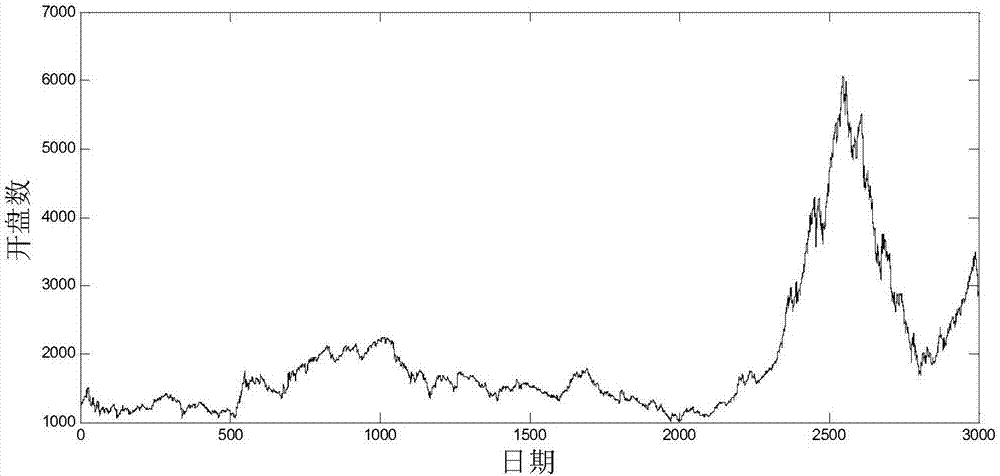
图2为原始时间序列数据图；

图3为人为添加异常值的数据图；

图4为中位数比值图；

图5为中位数法初步检测异常值后的图；

图6为eemd分解后的后7个分量叠加图；

图7为偏差比率图；

图8为eemd精细检测异常值后的图；

图9为曲线拟合校法正第一个区段异常值；

图10为曲线拟合校法正第二个区段异常值；

图11为曲线拟合校法正第三个区段异常值；

图12为曲线拟合校法正第四个区段异常值；

图13为曲线拟合校法正第五个区段异常值。

具体实施方式

下面结合附图对本发明的具体实施方式进行进一步的详细描述。

如图1所示，本发明提出的一种基于eemd的时间序列数据异常值检测和校正方法，步骤如下：

(1)对原始时间序列数据，按照时间顺序进行排序，对缺失数据用0值填补，得到初步整理数据；

(2)对所述初步整理数据进行异常值检测处理，把检测出的异常值用0值替换；

对初步整理数据进行异常值检测处理，包括如下步骤：

(2.1)通过中位数法对所述初步整理数据进行初步检测；

(2.2)通过eemd法对所述初步检测之后的数据进行精细检测；

(3)对异常值检测处理之后的数据进行异常值校正处理，即对数据中的0值进行填补，完成时间序列数据异常值检测和校正。对异常值检测处理之后的数据进行异常值校正处理，采用曲线拟合法实现。

所述的步骤2.1，通过中位数法对所述初步整理数据进行初步检测。

对于时间序列数据{ai}，i＝1,2,3,…,t，t表示时间序列的单位，根据实际研究对象，可能为天、小时等时间单位。

把{ai}中的正数选出来构成一个新的数列，记为把的中位数记为计算中每个数与中位数的比值若越大，则该日数据为异常大值的可能性越大；若越小，则该日数据为异常小值的可能性越大。

设定的阈值为r1,r2，若或者则为异常值，把异常值替换为0，原始的监测数据{ai}经过替换后得到的数列记为{bi}。阈值r1,r2可设置相对宽松一点，主要是为了把明显的异常大值和异常小值检测出来并替换为0，可减少这类明显的异常大值和异常小值对eemd分解的影响。

步骤3中异常值精细检测方法为集成经验模态分解法eemd。

把经过第一次异常值替换后得到的{bi}中的正数选出来构成一个新的数列且每个正数之间的排列顺序不变，把这样的数列称为正数组。再用eemd对进行分解，得到n个分量(包括n-1个imf和1个残余项rn)，频率依次从高到低排列，舍去高频分量，把后面m(1<m<n)个低频分量对应求和可得到一个新的数列，记为

m值的选取需要经过多次尝试，若m选取过小，与的偏差过大，会把正常值当做异常值检测，称为错检；若m选取过大，与过于接近，异常值就检测不出来，称为漏检。

根据经验，一般情况下，这里φ为黄金分割率，round为四舍五入取整函数)比较合适。从几何图像上看，当m选取的恰当时，既能很好接近中的正常值，又不受异常值牵引，从而既不会错检，也不会漏检。

为了量化与的偏离程度，定义偏差比率

越大，则该时间点的数据为异常值的可能性也就越大。

设的阈值为d0，即偏差比率大于d0的数据为异常值。也即当或者时，为异常值。经过异常值检测之后再把异常值替换为0，把{bi}经过异常值替换得到的数列记为{gi}。

所述的步骤4中异常值校正方法为曲线拟合法。

原始的监测数据{ai}经过两次异常值检测和替换变为{gi}，异常值都被替换为0，接下来需要对0值进行填补，也就是对异常值进行校正。本发明采用局部曲线拟合方法对0值进行填补。所谓局部曲线拟合方法是指对于每一段0值(包括单个0值，也可能是多个0值)前后端各选取一段序列(选取序列元素的个数可人为设定)，构成{gi}的一个子序列{hi}，对{hi}进行曲线拟合，方法是把{hi}中的正数选出来，得到一组样本点i+表示{hi}中出现正数的位置，采用多项式对样本点进行曲线拟合，得到的多项式记为f(x)。用曲线拟合值替换{hi}中的0值，i0表示{hi}中0值的位置。采用局部曲线拟合方法对{gi}的所有0值都进行填补，得到异常值校正后的结果。

实施例：

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。

步骤1：选取测试数据

选取公开数据为例进行验证分析。数据来源于王小川等编著的《matlab神经网络43个案例分析》第6章的上证指数数据。本发明选取其中的开盘指数这一列的后3000个数据。

步骤2：对原始时间序列数据作图

原始时间序列数据{ai}有3000个元素，这3000个元素排成一列，从上到下依次按时间递增的顺序排列，并标注好序号，序号从上到下依次为1到3000。对原始时间序列数据作图，如图2。用jarque-bera方法检验原始数据是否服从正态分布，结果显示不服从正态分布，说明不能用3sigma方法检测异常值。

步骤3：人为设置异常值

为了检验本文提出方法的有效性，人为把原始数据改变若干个值，使之成为异常值，设定的异常值信息如表1所示，

表1

共有17个异常值，分布在5个区段，异常值在序列中的位置表示改变为异常值的数据在原始时间序列数据中的位置。真实值表示原本的数据。异常值表示人为更改后的数据。异常值类型注明了该异常值属于哪种类型。异常值包括数据缺失(为0值)、粗大异常值、异常大值、异常小值。对改变后的数据如图3。

步骤4：中位数法异常值初步检测

把每个数据除以中位数对得到的比值如图4所示，可以看出大多数数据位于0.1到5之间。因此，设定异常值初步检测的条件为监测数据大于中位数的5倍或者小于中位数的0.1倍，经过这次异常值检测之后把异常值替换为0。原始的监测数据经过替换后得到序列{bi}，如图5。

步骤5：eemd法异常值进一步检测

把{bi}中的正数选出来构成正数组并保持正数组中每个正数的次序不变，用eemd对正数组进行分解，从高频到低频依次得到11个分量，包括10个imf和1个残余项rn。把后面7个低频分量对应相加得到一个新的数组(这里把11乘以0.618等于6.7980，再四舍五入取整得到7.)如图6所示。从图6可以看出后面7个低频分量叠加构成的数组能很好地拟合绝大部分正常数据，且不受异常值的影响。

计算偏差比率结果如图7。

从图7可以看出大部分偏差比率小于0.2，于是设的阈值为0.2，即偏差比率大于0.2的数据为异常值。经过第二次异常值检测之后把异常值替换为0。{bi}经过异常值替换后变为数列{gi}，如图8所示。

本例应用中位数-eemd方法对异常值进行检测，从检测结果可以看出17个异常值都被准确检测出，既没有错检也没有漏检。

步骤6：异常值校正

原始时间序列数据{ai}经过两次异常值检测和替换变为{gi}，异常值都被替换为0，接下来采用局部曲线拟合方法对0值进行填补。由于异常值分布在5个区段，因此对于这5个区段分别用曲线拟合方法填补0值。这里设定在每一个异常值区段的前面和后面分别选取20个不间断的数据构成一个子序列{hi}，对{hi}进行曲线拟合，用曲线拟合值替换{hi}中的0值，i0表示{hi}中0值的位置。5个区段异常值校正结果依次如图9、10、11、12、13所示，从上述5个图中可以看出校正后的值与真实值比较接近。校正后的数值结果如表2所示，

表2

可以看出校正后的值与真实值的相对误差较小，平均绝对百分误差(meanabsolutepercentageerror,mape)为1.57％，这里平均绝对百分误差的计算公式为

其中n为样本数，xi为真实值，为校正后的值。

本发明说明书中未作详细描述的内容属于本领域专业技术人员的公知技术。