缝式机匣处理参数化设计的优化方法与流程

本发明涉及的是一种航空发动机领域的技术，具体是一种缝式机匣处理参数化设计的优化方法。

背景技术：

航空发动机在宽广的工况中飞行时，其核心部件之一的压气机部件经常会遭受稳定裕度不足的困扰。稳定裕度过小会导致压气机极易进入非稳定工作状态，进而压气机性能严重下降，甚至发动机损坏。在当前航空压气机的负荷和效率要求越来越高的情况下，寻求改善压气机稳定裕度、推迟气流发生失速的流动控制方法愈加重要。机匣处理作为一种常用的被动控制技术，具有结构简单、制造成本低、可靠性高和扩稳效果好等优点，在众多的发动机型号中获得了成功的应用。

机匣处理的结构形式较多，以缝式机匣处理为例，其具有较多的几何设计参数，在设计机匣处理时，各个几何参数对流动控制的影响互相制约，尤其是机匣处理的关键几何参数对扩稳效果以及额外损失有着至关重要的影响，很难通过大量的多方案计算就找到使得压气机稳定裕度和效率都提高的最优设计。根据以往的经验，缝式机匣处理能有效提高压气机的稳定裕度，但是会以压气机设计点效率下降为代价。

技术实现要素：

本发明针对现有技术存在的上述不足，提出一种缝式机匣处理参数化设计的优化方法，通过对机匣处理进行参数化设计，给定合理的变量取值空间，采用以设计点效率和稳定裕度的多目标进行优化，得到最优的缝式机匣处理的结构，在确保设计点效率基本不下降的前提下，提高稳定裕度。

本发明是通过以下技术方案实现的：

本发明通过选定机匣处理需优化的几何参数变量及其对应的变化空间范围进行试验设计并构造代理模型，针对代理模型根据选定的优化目标采用多目标遗传算法进行多目标优化求解，通过数值模拟判断所得优化结果是否满足要求，将不满足要求的数值计算结果加入样本库中进行迭代求解，最终得到满足要求的具体几何参数。

所述的几何参数变量为：前缘轴向位置、尾缘轴向位置、机匣处理缝的深度、倾角、机匣处理的折角位置和开孔率。

所述的试验设计并构造代理模型是指：采用多维分层抽样方法撒布样本，对撒布的样本进行数值模拟求解控制方程，根据样本点选取代理模型进行构造。

所述的控制方程为：其中：为守恒型参数向量，t为时间坐标，为无粘矢通量，为粘性矢通量，q为源项。

所述的优化目标为稳定裕度和设计点效率。

所述的稳定裕度为其中：π和m分别为总压比和流量，下标ns表示近喘点，de表示设计效率点。

所述的设计点效率为其中：πde为设计点总压比，ede为设计点总温比。

技术效果

与现有技术相比，本发明提高了航空发动机压气机机匣处理的设计效率，缩短设计周期，降低研制成本，程序模块化处理，具有良好的扩展性，适合二次开发；并且优化计算的算例自动生成运行，节省了人力资源成本。

附图说明

图1为本发明流程图；

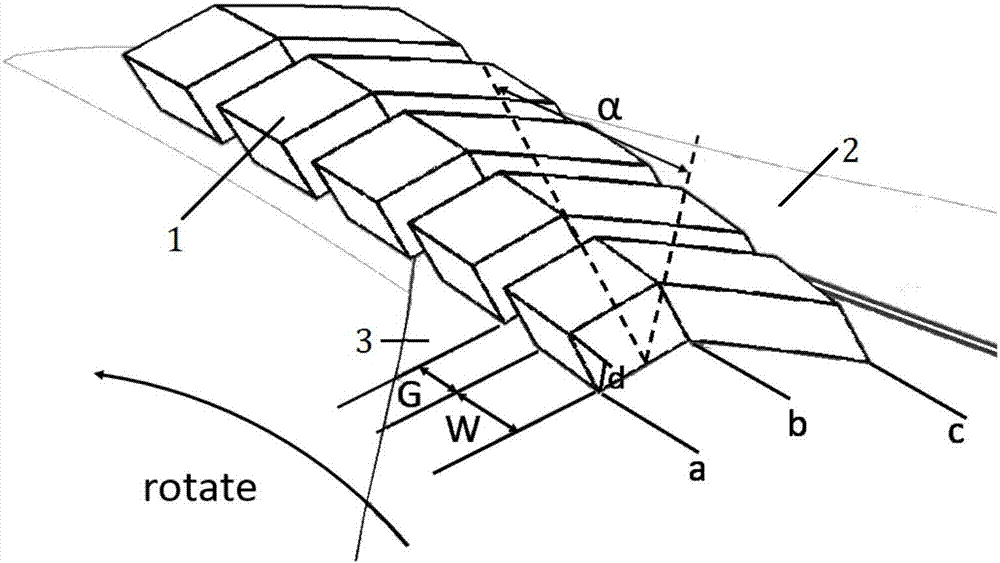
图2为机匣处理的几何参数示意图；

图3为优化的结果的pareto前沿解分布图；

图中：1为机匣处理缝，2为机匣，3为叶片。

具体实施方式

如图1所示，本实施例采用典型的轴流压气机的轴向折线斜缝机匣处理，具体包括以下步骤：

步骤1、选定机匣处理的需优化的几何参数变量及其对应的空间范围进行试验设计并构造代理模型。

如图2所示，所述的几何参数变量为：前缘轴向位置a、尾缘轴向位置c、机匣处理深度d、机匣处理倾角α、机匣处理折角位置(b-a)/(c-a)和机匣处理开孔率w/(w+g)。

所述的几何参数变量需要参考具体结构和流场给出，其对应的空间范围为：

1)前缘轴向位置a：取决于缝的轴向覆盖范围和缝所处的轴向位置，依据工程经验，缝2的轴向覆盖范围应小于等于叶片3尖端轴向弦长，缝所处的轴向位置应位于转子尖端的正上方或上游；

2)尾缘轴向位置c：结合前缘轴向位置和机匣处理缝1的轴向覆盖范围给定；

3)机匣处理缝1的深度d：深度范围选取需考虑发动机结构限制因素；

4)机匣处理缝1的倾角α：根据叶尖的流场确定缝在旋转方向上相对于子午平面倾角方向和角度；

5)机匣处理的折角位置(b-a)/(c-a)：兼顾网格生成过程中的可行性和优化范围的完整性；

6)机匣处理的开孔率w/(w+g)：0.5～0.8，并需考虑结构限制因素。

本实施例中各几何参数变量的取值范围如表1所示。

表1几何参数变量优化取值范围

其中：前缘轴向位置和尾缘轴向位置以压气机转叶前缘为零点，沿流向方向为正，s表示转子的叶尖轴向弦长。

本实施例的转子的叶尖轴向弦长s的值为45mm。

所述的试验设计并构造代理模型包括以下步骤：

s1：采用多维分层抽样方法撒布样本，对撒布的样本进行数值模拟求解控制方程。

所述的多维分层抽样方法为拉丁超立方(lhs)方法。

所述的拉丁超立方方法在表1所示范围内取出60个样本，采用参数化设计工具生成60个枰本对应的网格。

对选出的60个样本逐一进行雷诺平均navier-stokes方程的控制方程数值模拟求解，得到60个样本对应的稳定裕度和设计点效率。

所述的控制方程为：其中：为守恒型参数向量，t为时间坐标，为无粘矢通量，为粘性矢通量，q为源项。

所述的源项q包含哥氏力和离心力的作用。

将无粘矢通量和粘性矢通量分解至笛卡尔坐标系的分量：其中：和为笛卡尔坐标系中三个坐标轴的单位矢量。

则控制方程中各变量的形式为：其中：为速度项，τij为应力项，ω为相对坐标系的旋转角速度，ρ为密度，为静压，为总能量，qi为热流密度，为相对速度，r为半径，μ为粘性系数，μt为湍流模型引起的粘性系数修正，x为空间坐标量，κ为传热系数，κt为湍流模型引起的传热系数修正，t为温度，上标”^-”表示时间平均量，上标”^～”表示按密度平均的时间平均量。

考虑到湍动能的影响，静压和总能量的形式为：其中：k为湍动能，e为内能。

s2：根据样本点选取代理模型进行构造。

本实施例的代理模型为径向基神经网络(radialbasisneuralnetwork)，为一种局部神经网络，通过调整非线性函数的参数实现不同形状的基函数，通过这些基函数的加权线性组合来拟合目标函数。

采用有效样本对径向基神经网络进行训练，得到一个可以反映目标函数随几何变量变化规律的代理模型。

步骤2、对步骤1中的代理模型根据选定的优化目标采用多目标遗传算法进行多目标优化求解。

压气机的设计需要兼顾稳定性和效率，因此本实施例选择稳定裕度和设计点效率作为优化目标。

本实施例的多目标遗传算法为nsga-ii多目标遗传算法，得到代理模型的pareto前沿解，如图3所示，图中：sm为稳定裕度，de为设计点效率，sw为光壁条件，sample为样本点，opt为计算得到的最优解，样本点和最优解的结果组成了最终的解集。

所述的稳定裕度为其中：π和m分别为总压比和流量，下标ns表示近喘点，de表示设计效率点。寻优过程中以稳定裕度的最大值作为目标，最终以稳定裕度的提高百分比作为寻优结果的判断标准。

所述的设计点效率为其中：πde为设计点总压比，ede为设计点总温比。寻优过程中以设计点效率的最大值作为目标，最终以效率值的提高量作为寻优结果判断标准。

从前沿解上可以权衡稳定裕度和设计点效率，得到两者平衡提高的最优解，如表2所示。

步骤3、对步骤2得到的结果是否满足在确保设计点效率基本不下降的前提下，提高稳定裕度10％的要求进行分析判断筛选，将不满足要求的结果加入样本库中进行迭代求解，最终得到满足要求的具体几何参数。

从步骤2得到的前沿解上可以权衡稳定裕度和设计点效率，选取得到两者平衡提高的最优解，如表2所示。

表2机匣处理最优解具体几何参数和优化目标值

本实施例还可在非航空发动机领域的通用叶轮机械领域应用。

上述具体实施方式的应用环境为缝式机匣处理参数化设计的优化设计过程，具体操作中所涉及的参数包括机匣处理缝1的前缘轴向位置、尾缘轴向位置、深度、倾角、折角位置和开孔率，按照这些设置在具体环境中可以得到包括稳定裕度和设计点效率双目标的最优解的详细数值模拟结果。与现有的逐个调整六个设计参数的大量数值模拟技术对比，本实施例具有节省大量人力和时间成本且可以找出最优解的创造性优点。

上述具体实施可由本领域技术人员在不背离本发明原理和宗旨的前提下以不同的方式对其进行局部调整，本发明的保护范围以权利要求书为准且不由上述具体实施所限，在其范围内的各个实现方案均受本发明之约束。