一种基于分段非线性函数的风机功率曲线建模方法与流程

本发明属于风机功率曲线分析和建模领域，涉及一种基于风机功率曲线实际数据的，将混合整数规划引入以实现自动分段函数拟合功率曲线降低误差的方法。

背景技术：

风力发电在提倡新能源和清洁能源的二十一世纪，正在逐渐被各国政府和企业所重视。而在风力发电的领域内，风力发电机组的功率曲线作用举足轻重。功率曲线描述风速与机组输出功率之间关系，其不仅是风机设计过程中进行控制系统设计时的重要依据，更是考核风力发电机组性能、评估风力发电机组发电能力的一项重要指标。风机功率曲线对风机寿命、风机机组发电量以及风机性能检测等都有着举足轻重的作用。现有风电功率曲线的机理模型，但机理模型往往难以运用。于是现如今大多数功率模型是通过对风机实际数据进行模型拟合。

但是，基于实际数据拟合模型也面临一些问题：

(1)现如今常见的精度较高的四参数、五参数和七参数拟合方法在功率曲线的起始段和末尾段拟合效果较差，实际数据中，起始段有一段功率为零的数据带，而高风速的末尾段则会到达功率最大值呈现一段直线带，一头一尾的数据影响着中间数据的拟合；

(2)为了更好的拟合效果，通常在取线时将头尾去除，当作分段函数处理，此时需要提前增加程序步骤，同时人为的操作不能准确地找出分段点，影响曲线精度；

分段函数是一个函数在不同自变量定义的时候拥有不同的对应法则，在风机功率曲线上，低风速段的零点段和高风速段的满发功率直线段与中间部分的“s”形曲线在分界点处不连续，所以不存在只一个普通函数式就可以完美地拟合出一条完整的功率曲线，应用分段函数，有效地降低拟合带来的误差，不仅使中间部分的拟合曲线更贴近原效果，同时减少了在分界点处不连续带来的误差。一般的拟合函数如logistic函数对水平直线的拟合效果较差，采用分段函数可以有效地解决这个问题。

使用分段函数会产生上述的第二个问题，现今暂时解决去除头尾的问题有两个方法，一是通过人为地设定分界点，即通过对图形的大体印象，设定一个不变的常数作为两个分界点，但除了人为设定不精确之外，不变的常数不能适用于不同的风机，若不同的风机设定不同的常数又增加了工作量；而另一种方法是先采用类似四参数logistic方程进行拟合，将拟合出的曲线穿过横坐标轴和功率最大值的点设为分界点，但此时不仅增加了拟合的次数，同时这种分界点容易受到拟合方程原函数的约束，准确性下降。本发明采用整数规划来解决以上问题。整数规划是指一类要求问题中的全部或一部分变量为整数的数学规划。是近三十年来发展起来的、规划论的一个分支。整数规划问题是要求决策变量取整数值的线性规划或非线性规划问题。在整数规划中，如果所有变量都限制为整数，则称为纯整数规划；如果仅一部分变量限制为整数，则称为混合整数规划。整数规划的一种特殊情形是01规划，它的变数仅限于0或1。

技术实现要素：

有鉴于此，本发明的目的在于提供一种将混合整数规划和分段函数应用于大量风机运行实际数据相结合的模型计算技术，该方法采用了分段函数，通过设定两个分界点将风机功率曲线分为三段，有效地降低了风机功率曲线由于头尾的直线段对最后拟合效果的影响，同时直接采用风机的实际数据拟合，降低了由于实际环境、不同风机对风机功率曲线的影响。并利用混合整数规划，通过0-1规划将分段函数当做一个整体进行拟合，通过计算机自动优化寻找分界点，进一步提高了整个方法的精度和可靠性。

基于分段非线性函数的风机功率曲线模型，包括以下模块：数据采集模块，数据预处理模块；数据清洗模块；混合整数规划模块；分段拟合模块；数据分析处理模块。

基于分段非线性函数的风机功率曲线建模技术，它包含以下步骤：

步骤一：将数据按所需时间尺度进行读入，并通过简单的循环处理去除丢失参数和严重故障的数据，再将预处理后的数据进行数据清洗，清洗方法可采用oiv算法或者多倍均方差算法；

步骤二：设定所需的分段数，建立混合整数规划模型，将分界点当作变量列入模型之内，同时将零值、中间段拟合方程和最大值等加入到模型内，对同一台风机的大量数据使用整个模型进行自定义拟合，通过计算机自动优化寻找到分界点形成分段函数，同时每一段都进行非线性拟合，中间段拟合采用四参数logistic方程进行非线性拟合；

步骤三：对非线性拟合的风机功率曲线进行误差检验，通过拟合的函数方程计算如拐点等所需的数据，通过屏幕输出结果，同时保存拟合的结果。

本发明的有益技术效果为：本发明可以充分利用分段函数的特性，将不同的数据段用不同的函数进行拟合，有效地降低了不同风速段的数据集采用相同模型拟合带来的误差，同时采用混合整数规划将整个模型放入大量的实际数据进行拟合，能够一次性得到所有的分界点，降低了人为确认分段函数分界点的不确定性，相对于传统的使用实际数据进行取线拟合的方法，节省了采用bin法、最大似然法或者最大值法取线的步骤，同时也简化了数据后期处理分析的步骤，其任意分段的可扩展性也提高了该模型在不同风机的功率曲线建模下的适用性和可靠性。

附图说明

为了使本发明的目的、技术方案和有益效果更加清楚，本发明提供如下附图进行说明：

图1为本发明所述基于分段非线性函数的风机功率曲线建模技术的系统结构图。

图2为本发明所述基于分段非线性函数的风机功率曲线建模技术的系统模块图。

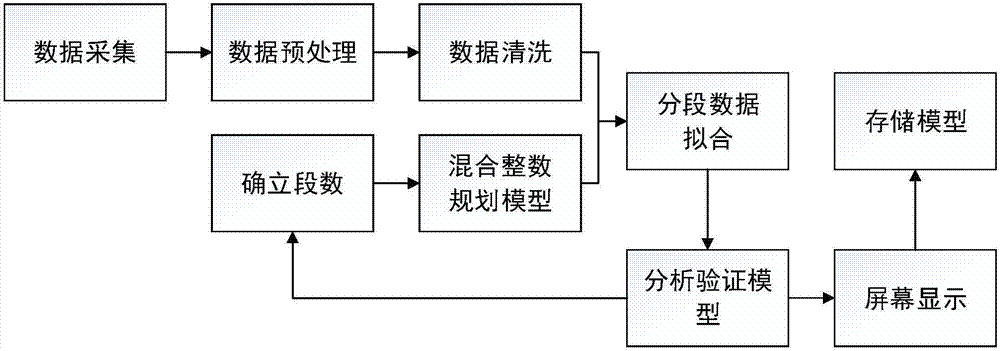
图3为本发明所述基于分段非线性函数的风机功率曲线建模技术的系统流程图。

具体实施方式

下面将结合附图，对本发明的优选实施例进行详细的描述。

图2为本发明所述基于分段非线性函数的风机功率曲线建模技术的系统结构图，包括以下模块：数据采集模块，数据预处理模块；数据清洗模块；混合整数规划模块；分段拟合模块；数据分析处理模块。数据采集模块根据预先设定的时间尺度将数据读取，数据预处理模块将大量选取的数据进行简单的处理例如去除负数点等，随后数据清洗模块对预处理后的数据进行清洗，同时混合整数规划模块根据所选的段数构建整数规划模型。随后分段拟合模块将混合整数模块自动优化得到的分界点进行分段拟合，数据分析处理模块对拟合结果进行误差分析，若误差较大，则重新选取段数拟合，若误差符合精度要求，则进行数据的后期分析处理、显示以及存储。

图3为本发明所述基于分段非线性函数的风机功率曲线建模技术的系统流程图，具体实现步骤如下：

(1)通过数据采集模块，设定风机实际运行数据的时间尺度(1分钟平均、5分钟平均、10分钟平均)，将大量实际数据读取到所设定的变量之中。

(2)数据预处理模块将一定时间尺度的数据读取进来后，通过设定的简单的逻辑循环结构，将数据分成多个风速比恩，对每一个比恩的数据进行数据筛选，将类似高风速零功率点的故障点以及与在同一比恩内平均风速误差过大的湍流点等先行去除。随后将处理过的数据保存在预定的变量或者文件之中。

(3)数据清洗模块对预处理后的数据进行清洗，采用改良后的滑差算法对预处理模块无法清洗的边缘点进行清洗，清洗过程为将数据等比例分为多个比恩，对每一个比恩内的数据进行排序，依次计算前i个坐标点中功率的方差值，并作为该点对应的滑差值，由于这种计算方式类似于滑动，故将计算结果形象地称为滑差值，所得到的数据集称为滑差集；最后，通过与初始阈值s比较分析实现数据清洗的功能。清洗过后，对数据进行检测，若故障点已基本消除，则继续运行，若仍存在大量故障点，则需重复清洗直到满足要求。

(4)数据清洗完成后，确定分段函数所分的段数，下面的步骤以分3段为例。

将曲线分为j1、j2、j3三段，同时设两个分界点的横坐标为f1、f2(f1＜f2)，其中f1是风机功率曲线的切入点，而f2是风机功率曲线的切出点，x是自变量风速，同时设两个状态量δ1、δ2。

则令：

则有非线性规划模型：

j＝δ1δ2j1+(1-δ1)δ2j2+(1-δ1)(1-δ2)j3

(5)分段拟合模块将预先设定的拟合函数代入进行拟合。

其中起始段j1和末尾段j3的拟合方程如下：

j1＝||0-y||

j3＝||pmax-y||

其中y为实际数据点的功率值，pmax是实际数据中功率的最大值，可以设pmax＝f(f2)，即最大功率值为切出点处的功率值。

中间段j2采用四参数的logistic方程，其式子为：

其中p、m、n、r为logistic方程的四个待定参数，x是自变量风速。

所以：

j2＝||f(x)-y||

将这些函数代入混合整数规划模型，使用自定义非线性拟合函数fittype对实际数据进行拟合，将优化计算得到的结果保存到设定的变量中。

(6)最后，数据分析处理模块将拟合的结果与原实际数据进行误差分析，若误差不满足实际要求，则重新设置段数或者重新设置不同的拟合函数进行拟合，直到误差达到系统的精度要求为止。

当误差达到所需精度后，即拟合效果满足要求，将处理过后的数据显示在屏幕上，并存储到预先设定好的变量或者文件之中，等待之后的处理。

最后说明的是，以上优选实施例仅用以说明本发明的技术方案而非限制，尽管通过上述优选实施例已经对本发明进行了详细的描述，但本领域技术人员应当理解，可以在形式上和细节上对其作出各种各样的改变，而不偏离本发明权利要求书所限定的范围。