基于局部精细接触模型的轴承等效径向刚度识别方法与流程

技术领域：

本发明涉及一种基于局部精细接触模型的轴承等效径向刚度识别方法，其属于系统参数识别领域。

背景技术：
：

轴承刚度定义为：轴承内外圈在产生单位相对弹性位移量时需要外加的负载。参照相对位移变化方向，可分为径向刚度、轴向刚度和角刚度等。对具有回转体的机械设备而言，其支撑轴承的刚度是决定轴承，轴，甚至整个系统使用寿命的关键性参数。通常情况下，在有限元分析阶段，为避免轴承滚子和内外圈的接触分析，我们把轴承的滚子简化为多排多个的弹簧单元，从而将识别轴承的等效刚度化作识别弹簧单元的刚度值。为获得该弹簧单元的准确刚度，一般需要对轴承进行相关试验(刚度测试试验或模态试验)。

毋庸置疑，上述常用的试验结合仿真的方法是获取准确轴承等效刚度、进行后续分析的有效保障，但当出现现场试验实施困难、试验成本太高、研究对象还处于设计阶段等情况时，找到某种有效方法代替试验来识别轴承的等效刚度很有必要，从而能在一定程度上保证有限元分析的准确性。

技术实现要素：
：

本发明在考虑轴承现场试验无法实施的情况下，提出一种基于局部精细接触模型的轴承等效径向刚度识别方法，能够一定程度上保证在有限元分析阶段进行轴承等效径向刚度准确性，有利于后期基于该轴承刚度的系统响应分析。

本发明所采用的技术方案有：一种基于局部精细接触模型的轴承径向刚度识别方法，步骤如下：

1)建立轴承局部精细接触模型，选取轴承最底端滚子的一半作为研究对象，建立其精细接触模型，即轴承局部精细接触模型；

2)建立轴承整体等效模型，在轴承内外圈之间建立多个弹簧-阻尼单元代替滚动体，并给弹簧-阻尼单元赋任意初始刚度值；

3)静力接触计算，分别在上述两个模型的中心点施加径向外载荷1/2q和fr，fr代表的是轴承整体受到的径向外载荷，q代表此时最底端滚子受到的载荷大小，两者的关系如公式(1)所示，其中z表示滚子的数量，在对应的载荷和边界条件下，分别对两个模型进行静力计算，观察两者的中心点径向位移量δ1和δ2

4)等效径向刚度识别，以局部精细接触模型的中心点径向位移量为标准，调整整体等效模型弹簧-阻尼单元的刚度值，使其中心点径向位移量与局部精细接触模型的中心点径向位移量相同，则认为此时弹簧单元总刚度值就是轴承整体在载荷fr下的径向刚度值；

5)改变外载荷fr大小，重新建立对应载荷下的局部精细接触模型，按照步骤3)和4)重新进行静力计算和等效径向刚度识别，得到多组载荷下的识别刚度值，从而拟合出轴承径向刚度随载荷变化的曲线，最终识别得到轴承等效径向刚度变化图；

6)设计合理的轴承模态试验方案，验证上述识别刚度的准确性。

进一步地，其中步骤6)具体包括：

a)设计试验方案：以轴-轴承结构为试验对象，采用力锤激励，加速度传感器采集信号，将信号输入到数据采集仪，最后传至计算机并记录，采用n-modal软件进行数据处理并识别出轴承试验结构的各阶模态频率与振型；

b)建立试验结构的有限元模型，参考步骤5)中的曲线，取试验载荷对应的刚度值代入有限元模型，进行模态计算，同样得到各阶模态频率与振型；

c)将相同振型下的试验模态频率和仿真模态频率进行比较，验证基于局部精细接触模型识别轴承径向刚度的有效性。

进一步地，步骤1)中轴承局部精细接触模型，其滚子和内外圈的接触区域网格大小要达到接触半宽的1/4到1/2才能达到精细模型的条件，其中，接触半宽根据赫兹理论公式(2)进行计算

其中，b表示接触半宽；l表示圆柱滚子长度；∑ρ为主曲率和；e1,e2表示两接触物体的弹性模量，μ1,μ2为泊松比。

本发明具有如下有益效果：

1)在没有试验或者试验实施困难的情况下，一定程度上依旧可以保证轴承径向刚度的准确性；

2)有利于后期基于轴承刚度的系统响应计算。

附图说明：

图1是本发明基于局部精细接触模型的轴承等效径向刚度识别方法的流程图。

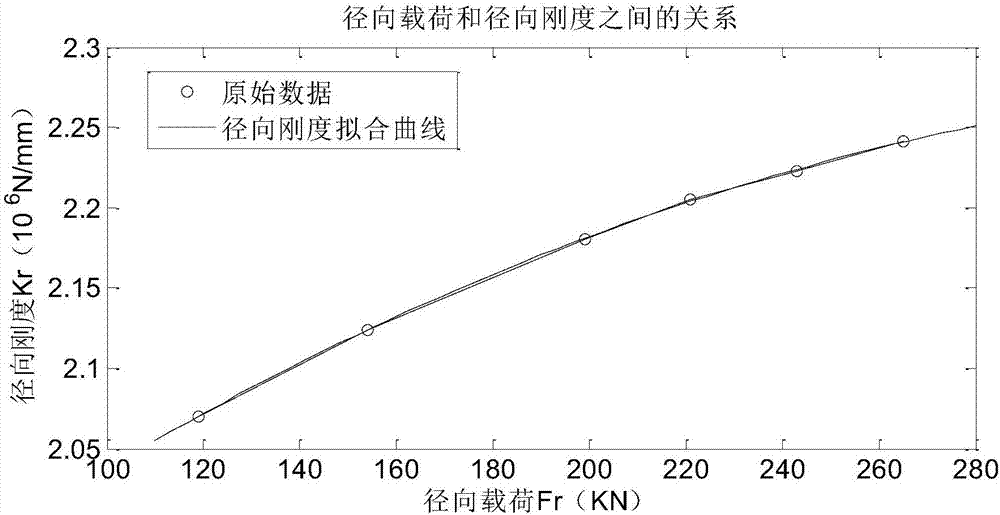
图2是本发明n222e轴承的径向刚度随径向载荷的变化图。

具体实施方式：

下面结合附图对本发明作进一步的说明。

本发明公开一种基于局部精细接触模型的轴承径向刚度识别方法，具体步骤如下：

1)建立轴承的局部精细接触模型。在不考虑游隙的情况下，考虑到精细模型网格的庞大和计算机处理能力，选取轴承最底端滚子的一半作为研究对象，建立其精细接触模型，即轴承局部精细接触模型。

2)建立轴承等效模型。建立轴承整体模型，在轴承内外圈之间建立多个弹簧-阻尼单元代替滚动体，并给弹簧单元赋任意初始刚度值。

3)静力接触计算。分别在上述两个模型的中心点施加径向外载荷1/2q和fr，fr代表的是轴承整体受到的径向外载荷，q代表此时最底端滚子受到的载荷大小，两者的关系如公式(1)所示，其中z表示滚子的数量。在对应的载荷和边界条件下，分别对两个模型进行静力计算，观察两者的中心点径向位移量δ1和δ2。

4)等效径向刚度识别。以局部精细接触模型的中心点径向位移量为标准，调整整体等效模型弹簧单元的刚度值，使其中心点径向位移量与局部精细接触模型的中心点径向位移量相同，则认为此时弹簧单元总刚度值就是轴承整体在载荷fr下的径向刚度值。

5)改变外载荷fr大小，重新建立对应载荷下的局部精细接触模型，按照步骤3)和4)重新进行静力计算和等效径向刚度识别，可得到多组载荷下的识别刚度值，从而可以拟合出轴承径向刚度随载荷变化的曲线，最终识别得到轴承等效径向刚度变化图。

6)设计合理的轴承模态试验方案，验证上述识别刚度的准确性。具体步骤包括：

a)设计试验方案：以轴-轴承结构为试验对象，采用力锤激励，加速度传感器采集信号，将信号输入到oros数据采集仪，最后传至计算机并记录；采用n-modal软件进行数据处理并识别出轴承试验结构的各阶模态频率与振型。

b)建立试验结构的有限元模型，参考步骤5)中的曲线，取试验载荷对应的刚度值代入有限元模型，进行模态计算，同样得到各阶模态频率与振型；

c)将相同振型下的试验模态频率和仿真模态频率进行比较，验证基于局部精细接触模型识别轴承径向刚度的有效性。

其中步骤1)中轴承局部精细接触模型，其滚子和内外圈的接触区域网格大小要达到接触半宽的1/4到1/2才能达到精细模型的条件。其中，接触半宽可根据赫兹理论公式(2)进行计算。

其中，b表示接触半宽；l表示圆柱滚子长度；∑ρ为主曲率和；e1,e2表示两接触物体的弹性模量，μ1,μ2为泊松比。

本发明以n222e型号的圆柱滚子轴承为例，部件包括轴承内圈、外圈和滚子，其局部精细接触模型有33123个3d单元，等效模型的组成单元包括2160个3d单元和90个弹簧-阻尼单元；具体步骤如下：

1)赫兹理论值计算：取径向负载fr＝119kn，根据赫兹理论计算公式(1)和(2)，得到此时作用在最底端的滚子承受的径向载荷q＝26.97kn；滚子和内圈的接触半宽b1＝0.356mm；滚子与外圈的接触半宽b2＝0.4128mm。

2)局部精细接触模型的建立：取n222e轴承最底端滚子的1/2作为局部研究对象，并在滚子与内外圈接触部分进行网格加密。由于只有当接触区域网格的最小尺寸大小要达到理论接触半宽的1/4～1/2才能保证计算结果在一定的误差范围内。所以在建立局部精细接触模型时，滚子与内外圈接触部分网格大小按照接触半宽的1/4取值为0.09mm，非接触区域网格大小为0.9mm。

3)局部精细接触模型静力接触分析：参照步骤1)中的计算结算，最底端滚子受力为26.97kn，1/2滚子受力大小为13.485kn，对此载荷下的局部精细接触模型进行静力接触计算，得到此时模型的中心点径向位移量为0.065mm。

4)建立轴承等效模型并计算：以整个n222e轴承为研究对象，利用弹簧-阻尼单元代替滚子建立轴承等效模型。静力计算时，静载荷大小不变为26.97kn，通过不断调整弹簧阻尼单元的刚度值，使轴承中心点位移和局部精细接触模型的弹性趋近量相同，即0.065mm，最终得到此载荷下的弹簧总径向刚度为2.07×10⁶n/mm，即该载荷下轴承的等效径向刚度为2.07×10⁶n/mm。

5)改变外载荷取值大小，根据公式(1)和(2)重新计算不同载荷下的接触半宽，取其1/4作为接触区域的网格大小重新建立局部精细接触模型，计算对应的中心点位移量。参照步骤4)中的方法识别不同载荷下的的轴承等效径向刚度，最终得到轴承径向刚度随径向载荷的变化图，如图2所示。

6)试验验证识别刚度的合理性：

a)设计试验方案：以轴-轴承系统为试验对象，利用压力机在轴承外圈上施压，使其径向刚度被完全激发，施加的外载荷大小为20kn。采用力锤激励，加速度传感器采集信号，将信号输入到oros数据采集仪，最后传至计算机并记录；采用n-modal软件进行数据处理并识别出轴承试验结构的各阶模态频率与振型。

b)建立试验所用的轴-轴承系统的有限元模型，轴承滚子依旧采用弹簧单元代替。参照图2，取20kn对应下的径向刚度值为1.87×10⁶n/mm，将其赋值给弹簧单元，进行预载荷下的模态计算。

c)将试验模态结果和计算模态计算进行对比，其中关注的两阶径向模态结果如表1所示：

表1试验和仿真模态参数对比

表1中的mac为模态置信因子，分析的是有限元模态与试验模态振型的相关性。一般情况下，mac值需满足大于0.7的条件。从表1中可以看出，两阶模态mac值都较高，频率误差也较小，说明上述刚度取值的合理性，从而证明了基于局部精细接触模型识别轴承刚度方法的有效性。

以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下还可以作出若干改进，这些改进也应视为本发明的保护范围。