一种基于拉马克获得性遗传原理的全局优化、搜索和机器学习方法与流程

本发明涉及计算机程序技术领域，包括人工智能，尤其涉及一种基于遗传算法的全局优化、搜索和机器学习方法。

背景技术：

为了解决全局优化、搜索和机器学习等技术问题，普通的遗传算法利用达尔文的“适者生存”自然进化法则，多次重复应用了三个算子：选择算子、交叉算子和变异算子，算法的搜索速度比较慢，搜索精度比较低；并且，遗传算法的局部搜索能力较差，导致算法在进化后期搜索效率低；在实际应用中，遗传算法容易产生早熟收敛的问题，采用何种选择方法既要使优良个体得以保留，又要维持群体的多样性，一直是遗传算法中较难解决的技术问题，限制了它在全局优化、搜索和机器学习中产生更大的技术效果。

技术实现要素：

为了克服基于达尔文“适者生存”自然进化法则的普通遗传算法的上述技术问题，本发明将拉马克获得性遗传原理和现代“表征遗传学”与达尔文进化论的“适者生存”自然法则相结合，构造“获得性遗传优化”技术方案和“获得性遗传算法”。首先，依据拉马克获得性遗传自然法则，发明一个获得性“遗传算子”及其“重写操作”方法，用来直接取代普通遗传算法的两个算子(即“选择算子”和“交叉算子”)，简化遗传算法的结构，克服目前遗传算法的多项技术缺陷，增强遗传算法的全局最优性和后期进化的可持续性。其次，依据拉马克用进废退自然法则，发明一个“用进废退算子”，可以用来取代普通遗传算法中的先天变异算子，从而在同一代内进行后天的定向变异操作，使变异操作产生新的技术效果，提升遗传算法的性能，使其解决全局优化、搜索和机器学习等问题更多、更好。

一种基于拉马克获得性遗传原理的全局优化、搜索和机器学习方法，包括如下步骤：

步骤1：根据优化、搜索和机器学习的问题对象构造目标函数f(x)；

步骤2：根据问题对象的优化需求，将问题对象编码成遗传算法的染色体，然后自动计算或手动输入遗传算法的运行参数，并进行算法初始化；此处的遗传算法为普通遗传算法；

步骤3：根据问题对象的优化需求，设第k代候选解种群为gk，且其中代表候选解种群gk中第i个染色体编码，s是种群大小。则利用迭代优化方法得到k+1代种群gk+1，即其中代表种群gk+1中第i个染色体编码，s是种群大小，优化过程如下：

(1)个体评价：计算候选解种群gk中每一个染色体编码解码后对应的目标函数值的大小；

(2)执行拉马克获得性遗传算子重写操作，产生临时种群g′k+1，包括如下步骤：

(2a)根据交叉遗传概率pc来从候选解种群gk中随机选择两个，然后比较两个染色体编码的目标函数值fmm和fn的大小，并计算基因遗传百分比pt：

pt＝fm/(fm+fn),fm>fn

(2b)计算遗传给下一代的基因数目nt为：

nt＝l·pt；

l为基因串的长度，pt为基因遗传百分比；(如果计算出的nt不为整数，则向上取整)

(2c)运行遗传算子，即执行重写操作：保留目标函数值大的染色体编码，将目标函数值大的染色体上的nt个基因对应重写到目标函数值小的染色体编码的相应位置上，形成新的染色体编码。对应重写即将目标函数值大的染色体编码上的选择位基因重写到目标函数值小的染色体编码的相应位置上，以此类推。

(2d)重复以上(2a)-(2c)过程pcs次，产生重写操作之后的临时种群g′k+1。s为种群大小，pc为交叉遗传概率。

(3)使用拉马克用进废退算子对临时种群g′k+1执行定向变异操作，获得新候选解种群gk+1；变异算子即普通遗传算法中的变异算子；

(4)重复迭代第(1)步到第(3)步，直到满足预先设定的终止条件；

(5)评价解码后该最优解是否满足此次优化计算的要求，若满足要求，获取最终优化解集；否则，修改运行参数，重新计算直到获取最终优化解集。

步骤4：输出问题对象的最终优化解集。

步骤2中，初始化的方法为：

(1)首先，根据遗传算法的运行模式，确定运行参数：候选解种群的大小s、变量维数d、变量取值范围、交叉遗传概率pc、变异算子中的内部参数；

(2)然后，根据优化需要，对问题对象进行编码，形成个体基因串、染色体和候选解种群,确定基因串的长度l。

(3)最后，根据问题对象的变量取值范围进行初始化，随机产生一组初始候选解，当k＝0，每个染色体基因组为即初始种群作为s为种群大小，d为变量维度。

在步骤2(2)中，对问题对象进行编码的方式为：如果d小于等于2，则选择二进制或十进制编码方法；如果d大于2，则选择实数编码方法。

目标函数值为针对最大化问题的适应度函数值或针对最小化问题的成本函数值。

在步骤3(1)中，个体评价使用多个处理器或多台计算机。

在步骤3(2)中，拉马克遗传算子重写操作时选取重写的nt个基因为随机选取。

在步骤3(3)中，变异操作采用普通遗传算法中的非定向变异方法，包括变异概率为pm的均匀变异方法，即不使用“用进废退算子”。

在步骤3(3)中，变异操作也可采用基于拉马克“用进废退”自然法则的“用进废退算子”，即实施定向变异方法。

在步骤3(3)中，“用进废退算子”可以采用梯度优化方法，如果梯度信息可以获得的话。在可获得梯度信息的情况下，根据梯度的符号和大小确定变异的方向和步长的方法。

在步骤3(3)中，“用进废退算子”可以采用非梯度优化方法。非梯度优化方法包括爬山算法、退火算法、单纯形方法(simplexmethod)、模式搜索(patternsearch)或鲍尔共轭定向法(powell'smethod)等。

在步骤3(2)和步骤3(3)中，每一代中的精英染色体编码不受拉马克遗传算子和变异算子改变，即保留精英，不重写与变异群体迄今为止参与进化而出现的最好个体(也称为精英个体，精英染色体编码)，而是在下一代中直接将其复制。确定精英的方法为普通遗传算法的方法。

在步骤3(5)中，评价最优解是否满足此次优化计算的要求，若满足要求，运算结束；否则，可以修改运行参数中的运行参数中的交叉遗传概率pc或变异算子中的内部参数，重复步骤3，获取问题对象的末代最优解集。

在步骤3(5)中，评价最优解是否满足此次优化计算的要求，若满足要求，运算结束；否则，还可以增大运行参数中的种群大小和/或迭代次数，重复步骤3，获取问题对象的末代最优解集。

在步骤2中确定的运行参数中的交叉遗传概率pc、变异算子中的内部参数，在步骤3的过程中，可以根据进化状态自动调整。

在步骤2中，染色体中的基因编码可以代表问题对象的结构或结构的数值参量。

通常，问题对象的构成包括问题对象的结构、每个结构的数值参量和结构之间的组合方式(其中有的用算数运算符或逻辑运算符表示)。在普通遗传算法中，染色体上的基因编码一般不是运算符；在“遗传编程”中，染色体上的基因编码可以是运算符。在本发明的步骤2中，问题对象的基因编码可以是运算符，从而使本发明的获得性遗传算法扩展到“获得性遗传编程”，实现能使问题对象的结构发生质变的自由优化。获得性遗传编程中的“遗传算子”类似于普通遗传编程的交叉操作，如图4所示，但是染色体的树状“剪枝嫁接”是通过用获得性遗传算法中的重写操作来来实现的。类似的，变异操作和“用进废退”可以将某一小分支由一个新的分支取代。因而，本发明的遗传算子和用进废退算子在获得性遗传编程中的实现方式并没有改变，但提高了遗传编程的速度和精度。这样，后天获得性遗传可以提高自由结构优化、自动编程尝试和机器学习功能。

本发明将拉马克获得性遗传原理和现代表征遗传学与达尔文进化论的适者生存自然法则相结合，构造获得性遗传优化的技术方案、获得性遗传算法及获得性遗传编程方法；发明操作拉马克获得性遗传自然法则的遗传算子来直接取代普通遗传算法的选择算子和交叉算子；还发明操作拉马克用进废退自然法则的用进废退算子来取代普通遗传算法中的先天变异算子；从而在同一代内进行用进废退的后天定向变异，使变异操作产生新的技术效果，使更多的全局优化、搜索和机器学习等问题得到更好的解决。具体呈现以下优点：

(1)优化过程结构简单，所需控制参数少，计算复杂度低，操作方便；

(2)增强了遗传算法和遗传编程的全局最优性和后期进化的可持续性；

(3)使全局优化、搜索和机器学习等问题的最优解集收敛更快，精度更高；

(4)具有更广泛的应用前景和领域：

1)复杂问题的优化，不要求有明确的数学表达式，因此它是解决这类问题的有力工具；

2)复杂系统分析，应用进化计算从事聚类分析、模式识别、图像处理、调度组织等工作，可将表面杂乱无章的复杂事物条理化；

3)自动控制。进化计算技术具有自适应、自学习、自组织的智能行为，能够适应环境变化，减少波动，保证高的控制精度，保证控制的实时性和快速性；

4)硬件自动设计，它能对复杂电路设计和自适应硬件领域提供一套全新的方法；

5)自动程序设计。基于遗传程序设计而开展的自动程序设计方法，正在发展成进化软件的研究，即不必精确地告诉计算机具体怎样去做，而由计算机自动完成。

6)综合应用。和其他技术相结合，各自发挥特长，综合解决问题。例如，将遗传算法和人工神经网络相结合，解决了机器学习等问题。

附图说明

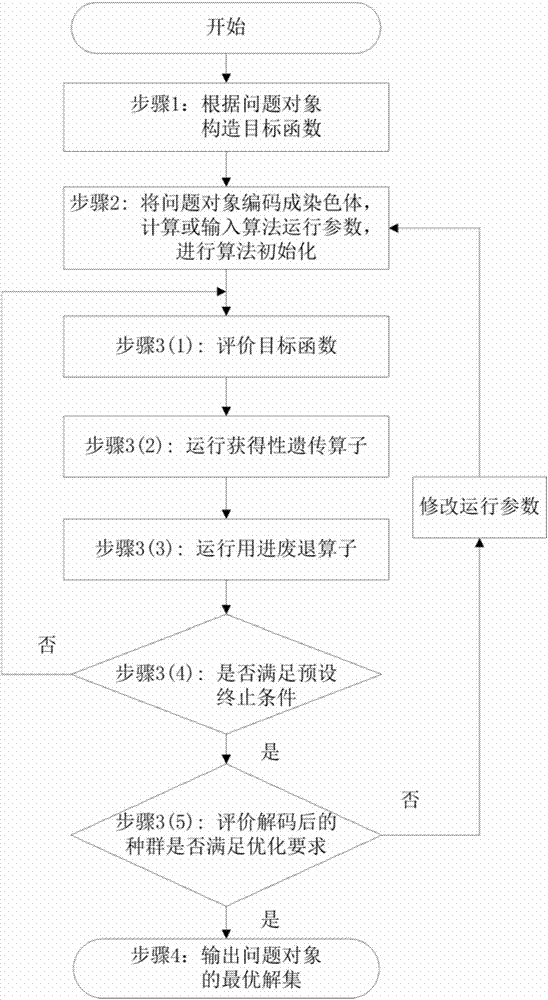
图1获得性遗传算法流程图

图2“遗传算子”重写操作流程图

图3一次重写操作示意图

图4获得性遗传编程的“嫁接繁殖”示意图

图5本发明和普通遗传算法在全局极小值(f1)优化和极大值优化(f2)中具体实施举例的算法适应度比较

图6本发明和普通遗传算法在全局极小值(f1)优化和极大值优化(f2)中具体实施举例的算法精度比较

图7神经网络机器学习示意图

图8神经网络实现2个变量异或问题示意图

图9最优和平均函数值

图10获得输出与输入关系

图11本发明的方法与其他粒子滤波算法在粒子数为10时的均方根误差均值对比曲线示意图

具体实施方式

实施测试

本实施测试通过选择全局优化、搜索和机器学习问题的标准函数对本发明和普通遗传算法进行性能测试和比较。标准函数以及相应参数设置如表1所示：

表1全局优化、搜索和机器学习问题的标准测试函数

¹xinyao.evolutionaryprogrammingmadefaster.ieeetransevolutionarycomputation,1999,3(2):82-101.

²michalewicz,z..geneticalgorithms+datastructure＝evolutionaryprograms,springer-verlag,berlin,1992.

通常，种群大小可以设置成变量数即维数的10倍，因此本实施的种群大小设为s＝300，普通遗传算法中交叉概率通常为pc＝0.5，变异概率通常为pm＝0.2。为了保持验证一致，本发明中的交叉遗传概率也取0.5，变异概率取0.2。对每个测试函数分别独立运行30次。函数评价次数都为3×10⁵。

对于两个测试函数，本发明提出的算法与普通遗传算法搜索解的均值、标准差、最优性以及精度结果分别如表2、表3所示：

表2全局优化、搜索和机器学习问题的标准测试函数f1下搜索结果比较

表3全局优化、搜索和机器学习问题的标准测试函数f2下搜索结果比较

由表2和表3的统计数据可以看出，本发明算法优化的均值、标准差、最优性和精度都要优于普通遗传算法，且在解的精度上要超出很多，与理论最优值接近程度高。

图5和图6分别显示了本发明和普通遗传算法随着函数评价次数变化的平均适应度及平均搜索精度关系。从图中可以看出，本发明算法在优化测试函数f1和f2时，得到的优化解更接近于理论最优解，同时本发明算法的搜索速度比普通遗传算法也快很多。

综上可以得出，本发明具有较高的优化精度和较快的收敛速度。

为了便于公众理解及使用本发明的技术方案，下面以两个全局优化、搜索和机器学习问题的应用实例来进行进一步说明。

应用实例1–基于简单神经网络的异或机器学习问题

人工神经网络(artificialneuralnetworks，简写为anns)也简称为神经网络(nns)，它是一种模仿动物神经网络行为特征，进行分布式并行信息处理和机器学习的算法模型。这种网络依靠互联的非线性神经元节点，通过调整节点之间相互连接的关系和权重，达到处理信息和学习、记忆的目的。图7显示了一个简单的神经网络，圆圈表示神经元，输入点“-1”被称为偏置节点。神经网络最左边的一层是输入层，最右的一层是输出层。中间所有节点组成隐藏层，我们不能在训练样本集中直接观测到它们的值。同时可以看到，该神经网络机器学习的实施例子中，有2个输入单元(偏置单元不计在内)，2个隐藏单元及一个输出单元。

如图8所示，这里用一个具有简单网络的神经网络实现2个变量的异或问题，来说明使用获得性遗传算法的机器学习情况，对寻找出实际而又有效的学习算法具有重要的示范意义。其中输入神经元为x1、x2,输出为y,则异或问题的4种训练模型如表4所示。

表4异或问题的训练模型

输入层神经元到输出层神经元的连接权值共有9个，记作wn,n＝1，2，…，9。

利用本发明的全局优化、搜索和机器学习技术方案解决神经网络实现异或问题，训练网络的权值wn，具体实施流程如图1和图2所示：

步骤1：根据异或问题构造目标函数f(w)，w为权向量,即w＝{wn，n＝1，2，…，9}。不失一般性，这里采用其中m是训练模型编号，ym表示训练模型m的输出，由图8知f是w的函数，其值代表了解的适应度，它越大，训练或学习误差越小。所以，此实例的目标是使f最大化。

步骤2：根据问题对象的优化需求，自动计算或手动输入普通遗传算法的运行参数，将w编码成染色体，并进行初始化：

(1)首先，根据普通遗传算法的运行模式，s＝90(一般可以取参数变量维数的10倍)、变量维数d＝9、w取值范围从-5到4.9、遗传概率采用pc＝0.6、变异概率采用pm＝0.05；

(2)然后，对问题对象需要优化的结构及其参数进行十进制编码，形成个体基因串、染色体和候选解种群，确定基因串的长度l；这里采用两位十进制数描述权值的编码方案，具体如表5所示，这样基因串的长度l＝2×d＝2×9＝18。比如，w＝{w1，w2，w3，w4，w5，w6，w7，w8，w9}＝{-5，-4.9，-4.8，-4.7，0.0，4.6，4.7，4.8，4.9},则它的编码格式为we＝{000102035096979899}。

表5权值的两位十进制编码

(3)最后，根据问题对象的变量取值范围进行初始化，随机产生一组初始候选解。当k＝0，每个染色体为权值向量的编码格式则为编码的每一位，初始种群作为

步骤3：根据优化需求，假设第k代种群为代表种群中的一个个体(染色体)，则利用迭代方法，通过重写、变异操作就能得到k+1代种群优化过程如下：

(1)个体评价：根据表4，训练输入矩阵期望输出矩阵y＝[0101]，计算种群gk中每一个个体解码后的适应度，即目标函数值，这里属于最大值问题。比如，则比优越。

(2)执行拉马克“遗传算子”重写操作产生新候选解种群g′k+1，如图2所示，包括如下步骤：

(2a)根据交叉遗传概率pc，随机选择两个父代染色体(即父代候选解的基因串)，即随机产生一个(0,1]之间的随机数r，如果r<pc，则选取两个父代染色体，否则不选取，继续产生随机数r。例如和

(2b)比较两个染色体适应度函数值和假如，则将给子代遗传相对更多的基因。计算基因遗传百分比pt:

那么根据下式计算遗传给下一代的基因数目nt为

(2c)运行遗传算子，执行重写操作：保留适应度强的染色体，将适应度强的染色体上的nt个基因对应重写到适应度弱的染色体的相应位置上，形成新的染色体。对应重写即将适应度强的染色体上的选择位基因重写到适应度弱的染色体的对应位置上，以此类推，基本流程图如图2所示，一次重写操作的示例如图3所示(图中未标出所有编码位)。根据上个步骤，那么中有18×2/3＝12个编码位被中的编码位重写后为一次重写。

(2d)重复以上(2a)-(2c)过程pcs次，产生重写操作之后新候选解的临时种群g′k+1；

当重写次数大于或等于np＝pcs(0.6×90＝54；如果积不是整数，则向上取整)时，重写操作结束，当重写次数小于54，继续重复(2a)-(2c)。

(3)使用一个适当的“变异算子”，对临时种群g′k+1执行变异操作，获得新候选解种群gk+1；这里的机器学习问题比较简单，因而此实例中没有采用“用进废退”操作，而只需采用比较常用的普通遗传算法中的先天均匀变异方法。因为变异概率pm＝0.05，一次迭代后的新种群gk+1中将有90×18×0.05＝81(如果积不是整数，则向上取整)个编码位获得一个介于并包括0到9之间的新值。

(4)重复迭代第(1)步到第(3)步，直到满足预先设定的终止条件。此处终止条件简单地设为进化100代。

(5)评价解码后该最优解是否满足此次优化计算的要求，若满足要求，运算结束；否则，修改算法的运行参数，比如手动修改交叉遗传概率pc变异概率pm，或者增大种群大小和进化迭代次数，重新计算，获取最终优化结果。此处优化计算的要求为f>0.95，图9显示已满足要求。

步骤4：输出问题对象的末代最优解集w0。如图8所示，也显示了一个权值的最优解集。

图9和图10分别显示了本发明优化神经网络来实现2变量异或机器学习的问题时，迭代100次最优和平均目标函数值以及获得的输入输出关系。从图中可以看出，本发明算法在优化神经网络异或问题权值时，得到的输出能较好地接近于期望输出。

综上可以得出，本发明的获得性遗传算法能很好地优化神经网络、搜寻最优权值和解决机器学习问题。

进一步地，如图7所示的网络结构也可以编码入基因串，从而与权值同时优化。

如果问题对象需求的网络结构更加复杂，可以实施获得性遗传编程，则网络结构还能得到更直接、更自由的优化。

应用实例2-信号处理问题

粒子滤波算法是非线性信号处理中的一个重要技术，它不受系统模型特性和噪声分布限制，从而比其它的滤波技术具有更广泛的适用性。然而，粒子滤波算法的性能受自身粒子贫化问题的限制。利用本发明的算法解决粒子滤波算法重采样过程的粒子匮乏问题，优化粒子分布，使得粒子样本更接近于真实后验概率密度样本，提高滤波性能。

这里通过粒子滤波实现一个非线性动态系统的状态估计，来说明使用获得性遗传算法的优化粒子滤波处理信号情况，对寻找出性能优越的非线性滤波算法具有重要的意义。其中系统的状态空间模型如下：

xk+1＝1+sin(0.04πk)+0.5xk+vk

其中，过程噪声vk～gamma(3,2)，观测噪声nk～n(0,0.00001)。设定观测时间为70，运行次数为200，粒子数n为10。

利用本发明的全局优化、搜索和机器学习技术方案解决粒子滤波算法粒子贫化问题，优化粒子分布，具体实施方式如下：

步骤1：根据非线性动态系统的状态估计问题构造目标函数f(x)，这里选用粒子的权值函数；

步骤2：根据问题对象的优化需求，自动计算或手动输入普通遗传算法的运行参数，并进行初始化：

(1)首先，根据普通遗传算法的运行模式，确定种群大小s＝n＝10,n为粒子数目、变量维数d＝1、交叉遗传概率pc＝0.9、变异概率pm＝0.05；

(2)然后，对问题对象需要优化的结构及其参数进行编码，形成个体基因串、染色体和候选种群，确定基因串的长度l；这里采用固定有效位数lx＝7的浮点数编码每个重要性采样粒子值，即系统的状态值x，每个染色体表示一个粒子浮点数格式，浮点数值的第一位代表符号位，“1”代表正数，“0”代表负数，其中基因串长度即为固定有效位数，即l＝d×lx＝1×7。比如，k时刻第i个粒子状态值x＝10.4711那么它的浮点数编码格式为xc＝(1104711)。

(3)最后，根据问题对象的变量取值范围进行初始化，随机产生一组初始候选解。这里就根据粒子自身初始化步骤随机产生。当k＝0，每个染色体为粒子状态值的编码格式则为编码的每一位，初始种群作为

步骤3：根据优化需求，假设当前(第k代)种群为代表种群中的一个个体(染色体)，则利用迭代方法，通过重写、变异操作就能得到k+1代种群优化过程如下：

(1)个体评价：根据粒子权值公式，计算种群gk中每一个个体解码成x后的适应度，这里属于最大值问题。比如

(2a)根据遗传概率pc，随机选择两个父代染色体(即父代候选解的基因串)，例如和

(2b)比较两个染色体适应度函数值和假如，则将给子代遗传相对更多的基因。计算基因遗传百分比pt:

那么根据下式计算遗传给下一代的基因数目nt为

nt＝l·pt＝7×3/5≈5(这里实施了向上取整)

(2c)运行遗传算子，执行重写操作：保留适应度强的染色体，将适应度强的染色体上的nt个基因对应重写到适应度弱的染色体的相应位置上，形成新的染色体。对应重写即将适应度强的染色体上的选择位基因重写到适应度弱的染色体的对应位置上，以此类推，基本流程图如图2所示。根据上个步骤，那么中将有7×3/5≈5个编码位被中的编码位重写。

(2d)重复以上(2a)-(2c)过程pcs次，产生重写操作之后新候选解的临时种群g′k+1。

(3)使用一个适当的“变异算子”，对临时种群g′k+1执行变异操作，获得新候选解种群gk+1；由于这里机器学习非线性滤波的问题相对复杂，因而此实例中考虑“变异算子”采用“用进废退”操作。

(3a)一般地，可以采用普通遗传算法中比较常用的非定向的均匀变异方法。因为变异概率pm＝0.05，一次迭代后的新种群gk+1中将共有10×7×0.05≈4(这里实施了向上取整)个编码位进行变异，其中如果随机选择的变异位是编码的符号位，则按照普通遗传算法的二进制变异，即其可能由1变0，或由0变1。除去符号位的变异位获得一个介于0到9之间的新值。

(3b)为了提高滤波算法的速度和精度，在此举例说明普通遗传算法中的非定向的“变异算子”怎样采用获得性遗传算法中的定向的“用进废退”算子来实现。在这个应用实例中，用非梯度优化的爬山算法来实现“用进废退”操作。对新种群gk+1中的个体与均匀变异方法相似，变异概率同样选为pm＝0.05，但与非定向变异不同的是，这里是对新种群gk+1中个体解码成对应的粒子状态值进行操作，即一次迭代后将有10×0.05≈1(这里实施了向上取整)个粒子状态进行变异，变异的粒子状态获得一个原粒子状态值附近的随机新值。且定向变异是对所要变异的粒子状态值进行nm次变异而取最佳结果。这里nm＝s×20％＝10×20％＝2，通过2次变异后得到的2个新粒子状态值与原来的对比，取最佳结果，即形成定向变异。因此，变异总是向着不更差的方向进行，实现“用进废退”。

(4)重复迭代以上步骤3中的第(1)步到第(3)步，直到满足预先设定的终止条件。

(5)评价该最优解是否满足此次优化计算的要求，若满足要求，运算结束；否则，修改算法的运行参数，增大种群大小和迭代次数，重新计算，获取最终优化结果。

步骤4：输出问题对象的末代最优解集,即粒子集。

表6显示了粒子数目n＝10的情况下进行200次蒙特卡罗实验，统计本发明和其它几种粒子滤波算法，即基本粒子滤波算法(pf)，辅助粒子滤波算法(apf)和正则化粒子滤波算法(rpf)，进行均方根误差(rmse)均值、rmse方差的比较结果。

表6：n为10的粒子滤波试验结果

图11显示了本发明与其它粒子滤波算法所产生的rmse均值随时间变化图。从表6和图11都可以看出，本发明的获得性遗传算法能很好地优化粒子滤波、搜寻最优粒子集和解决非线性滤波问题。