一种大数据环境下的数据优化及快速抽样方法与流程

本发明涉及大数据分析领域，尤其是涉及一种大数据环境下的数据优化及快速抽样方法。
背景技术：
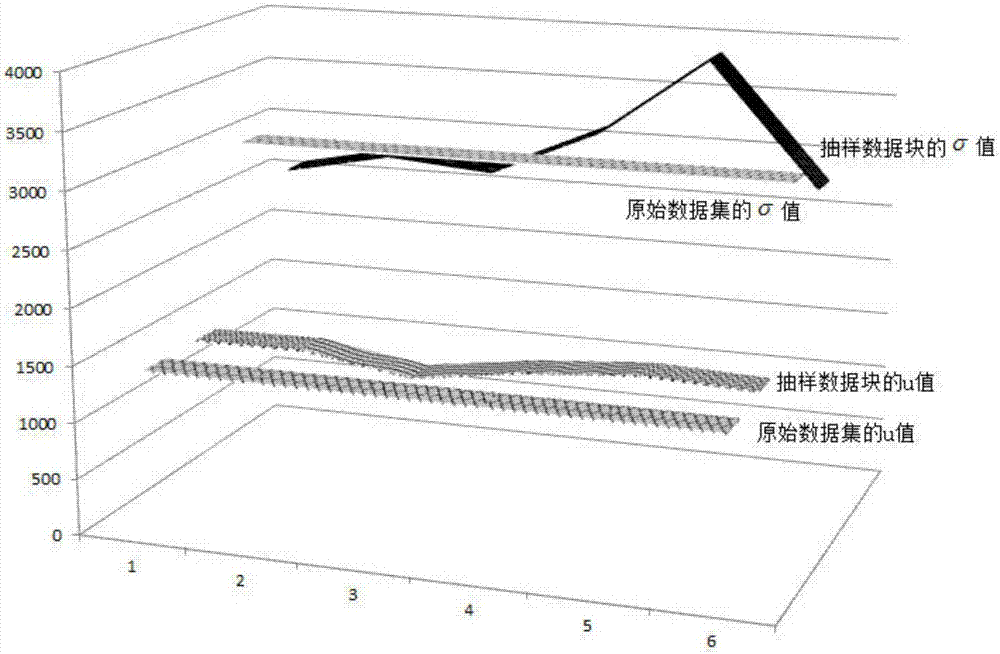
：医疗和电子商务应用的激增产生了巨大的数据量，把人们带入了“大数据”时代。与传统的大数据集不同，“大数据”一词不仅意味着数据量的大，而且还表示数据的生成速度快。然而，目前的数据挖掘和分析技术面临着在一个挑战，即在很短的时间内处理大容量数据，大数据时代的到来促使研究人员寻找解决大量数据的优化的解决方案，特别是对在线商业和医疗数据的解决方案。现有技术中，处理大数据集的体积通常采用的方法是：采用矩阵分解的方法，通过减少数据列(降维)，然后应用增强的紫外分解方法来分割大数据集，将分隔后得到的数据块进行分析，但是对于一个非常大的数据集，矩阵分解方法并不能减少大数据集体积，也没能提高数据的处理效率。经过大量国内外文献、实际应用及专利资料的查阅，发现与本发明提出的原理及应用开发尚无类似相同的技术。技术实现要素：本发明所要解决的技术问题是提供一种大数据环境下可以减少数据体积、并且能够提高数据处理效率的数据优化及快速抽样方法。本发明所采用的技术方案是，一种大数据环境下的数据优化及快速抽样方法，包括以下步骤：(1)、数据预处理，将大数据集部署在云环境中，按照数值属性将大数据集划分成若干列子数据集，即具备相同数值属性的数据归入到同一列子数据集中，所述子数据集的形式包括数值形式子数据集和文本形式子数据集，将数值形式的子数据集从大数据集中筛选出来；(2)、从筛选出来的若干子数据集中选择出需要进行分析的某一个子数据集，在本地系统下建立一个保存路径，将该子数据集进行保存，并对该子数据集做曲线拟合；(3)、将该子数据集拟合得到的曲线进行判断，如果该曲线的分布形式近似正态分布曲线，执行步骤(4)；如果该曲线的分布形式近似泊松分布曲线，那么执行步骤(5)；(4)、设置需要对该子数据集进行分割的数据块数量，使用正态分布的分割方法对该子数据集进行分割得出若干数据块，从若干数据块中抽样某个数据块，执行步骤(9)；(5)、将拟合近似泊松分布的原始曲线朝纵坐标的方向上移k个单位得到曲线a，再将近似泊松分布的原始曲线朝纵坐标的方向下移k个单位得到曲线b，曲线a与曲线b之间的区域形成一个标准区域；(6)、设置需要对该子数据集进行分割的数据块数量，根据数据块数量来对该子数据集中的数据总数据量进行平均分割，即每个分割得到的数据块所包含的数据量＝子数据集的总数据量/数据块数量；(7)、从分割得出的若干数据块中抽取出某一个数据块e，并对该数据块进行曲线拟合，看该数据块拟合得到的曲线是否落在曲线a与曲线b之间形成的标准区域内，如果数据块的曲线落在标准区域内，那么就执行步骤(9)；如果数据块的曲线没有落在标准区域内，就执行步骤(8)；(8)、任意选择一个样本数据，该样本数据位于除数据块e以外的其他数据块中，如果该样本数据加入到数据块e中，能够使数据块e拟合的曲线位于标准区域内，那么就将该数据点列入数据块e中；如果该样本数据加入到数据块e中无法使数据块e拟合的曲线位于标准区域内，就继续选择样本数据放入数据块e中，直到数据块e的拟合曲线位于标准区域内为止，并执行步骤(9)；(9)、对得到的该数据块进行数据分析。本发明的有益效果是：从海量数据中筛选出需要进行分析的具备某个属性的子数据集，然后对该子数据集进行优化，最终选取某个小型的数据块来进行数据分析，这种方式极大地缩小了数据体积，缩短了数据分析时间。如果子数据集的拟合曲线近似正态分布，那么通过正态分布算法对子数据集进行分割得出的数据块也是符合正态分布，那么只需要从抽样分割得到的数据块来进行分析就能得出所属子数据集以及海量数据所蕴含的信息内容，提高了数据分析效率，并且也提高了数据分析的准确性；如果子数据集的拟合曲线近似泊松分布，那么对子数据集进行平均分割后，抽取其中某数据块进行优化后符合了泊松分布，那么从抽样分割得到的该数据块来进行分析就能得出所属子数据集以及海量数据所蕴含的信息内容，提高了数据分析效率。作为优先，大数据集表示为a[1,k]，设定大数据集中的其中某一个数值形式的子数据集为s[a,b]，假设子数据集中的某个数据x∈[a,b],并且满足：其中μ为均值，σ为标准方差，那么可以得出子数据集满足：即可以得出该子数据集是服从正态分布。作为优先，设定子数据集的位置为s(pl,pr),pl和pr均表示位置，且的绝对值小于δ，其中p表示最大数值的位置点，δ表示进行分块时，指针向某数据块集合两边进行调整的最大范围值，以a(p)来表示子数据集s[c-δ,c+δ]中的最大的可能性数值，c＝(pl+pr)/2＝pl+b/2,b＝k/m，c表示子数据集的中间位置，m表示分割的数据块数量，由a(p)∈s，假设s[a,b]满足：a(p)＝max(s),c≈(a+b)/2,|c-p|≤δ，，则可以得出s[a,b]为包含一系列服从正态分布的数据块的子数据集，即：其中mr为可动态调整的m参数值，在初始化m值后，随着δ调整分块，m值发生变化，分割过程中剩下的区域由mr来调整，其中xi表示一个左侧相邻区间被动态调整的数据集合内选择的该区间的频率最大值所在的位置值减去此区间左侧相邻的上部区间的位置值。作为优先，所述步骤(4)中描述的正态分布的分割方法为：第一、先设定一些特定的初始化值，即设定整体子数据集为s[1，n]，设定δ表示进行分块时，指针向进行分割的数据块集合两边进行调整的最大范围值，设m表示分割的数据块数量，则b＝n/m表示每个数据块的长度，设lp表示不符合条件的分割点的最大值，设pl为当前进行分割的数据块集合的最左侧位置，设pr为当前进行分割数据块集合的最右侧位置，即pr＝b，设c为当前进行分割的数据块集合的中心位置，即c＝b/2,设cl＝c-δ,cr＝c+δ，即cl表示数据块中心向左移动δ，cr表示数据块中心向右移动δ，设定p＝maxpoint(s,cl,cr，lp)，p表示当前进行分割的该数据块中最接近分割点的点位置，lp表示该数据块中最接近分割点的点的最大值；第二、开始进行分割，从默认第一个数据块开始进行分割，当pr满足pr≤n时，如果|p-c|＞δ，则得出lp＝[lp,p]，p＝maxpoint(s,cl,cr，lp)，即表示确定出该数据块中最接近分割点的点位置，然后在这个点位置附近用cl和cr来做调整找出分割点的位置，在数据块中心向左或向右移动之后确定出分割点，然后再进行分割下一个数据块，需要分割出的数据块的各个参数值为上一个分割得出的数据块调整后的参数值，直到分割出第m个数据块为止。采用正态分布算法的方法进行分割，得出的数据块的数据依然是符合正态分布，并且可以支持支持快速查询进行分割的数据块，提高了分析大数据集的包容性。作为优先，所属数值形式的子数据集的数量至少为一列，因为只有增加更多的数字数据才可以提高大数据分析结果的准确性。附图说明图1为本发明实施方式中正态分布时数据集1中的参数对比；图2为本发明实施方式中正态分布时数据集2中的参数对比；具体实施方式以下参照附图并结合具体实施方式来进一步描述发明，以令本领域技术人员参照说明书文字能够据以实施，本发明保护范围并不受限于该具体实施方式。本发明涉及一种大数据环境下的数据优化方法，包括以下步骤：(1)、数据预处理，将大数据集部署在云环境中，按照数值属性将大数据集划分成若干列子数据集，即具备相同数值属性的数据归入到同一列子数据集中，所述子数据集的形式包括数值形式子数据集和文本形式子数据集，将数值形式的子数据集从大数据集中筛选出来；(2)、从筛选出来的若干子数据集中选择出需要进行分析的某一个子数据集，在本地系统下建立一个保存路径，将该子数据集进行保存，并对该子数据集做曲线拟合；(3)、将该子数据集拟合得到的曲线进行判断，如果该曲线的分布形式较接近正态分布曲线，执行步骤(4)；如果该曲线的分布形式较接近泊松分布曲线，那么执行步骤(5)；(4)、设置需要对该子数据集进行分割的数据块数量，使用正态分布的分割方法对该子数据集进行分割得出若干数据块，从中抽样某个数据块，执行步骤(9)；(5)、将拟合接近泊松分布的原始曲线朝纵坐标的方向上移k个单位得到曲线a，再将接近泊松分布的原始曲线朝纵坐标的方向下移k个单位得到曲线b，曲线a与曲线b之间形成一个标准区域；(6)、设置需要对该子数据集进行分割的数据块数量，根据数据块数量来对该子数据集中的数据进行平均分割，即每个分割得到的数据块所包含的数据量＝子数据集的总数据量/数据块数量；(7)、从分割得出的若干数据块中抽取出某一个数据块e，并对该数据块进行曲线拟合，看该数据块拟合得到的曲线是否落在曲线a与曲线b之间的标准区域，如果数据块的曲线落在标准区域内，那么就执行步骤(9)；如果数据块的曲线没有落在标准区域内，就执行步骤(8)；(8)、任意选择一个样本数据，该样本数据位于除数据块e以外的其他数据块中，如果该样本数据加入到数据块e中，能够使数据块e拟合的曲线位于标准区域内，那么该数据点就是需要的点；如果该样本数据加入到数据块e中无法使数据块e拟合的曲线位于标准区域内，就继续选择样本数据放入数据块e中，直到数据块e的拟合曲线位于标准区域内为止，并执行步骤(9)；(9)、对得到的该数据块进行数据分析。将大数据集部署在云环境中，分布式的云计算环境允许在本地系统下来分析和处理数据，子数据集可以分布在任何云框架的不同位置，然后通过单个云节点来处理其本地系统下的子数据集，此外，子数据集分割适用于云环境中并行处理,增加内存使用的灵活性。每个子数据集的数值属性可以是年龄、持续时间、出生体重、人口分布的身体质量指数、乳腺癌病人的人口数量分布、家庭住址、日期、性别等等，其中比如年龄、日期、性别、家庭住址这种类目的数据属于文本形式的子数据集，而持续时间、出生体重、人口分布的身体质量指数以及乳腺癌病人的人口数量等这些数字形式的类目属于数值形式子数据集，这类子数据集需要从大数据集中筛选出来再来做分析处理，采用本发明所述的数据优化方法的先决条件是大数据集需要包含至少一个数值形式的子数据集列，对筛选出来的子数据集进行曲线拟合，看该曲线的分布形式是接近正态分布还是泊松分布，如果接近正态分布，那么使用正态分布的分割方法分割子数据集从而创建小而且具有代表性的数据块，所得出的数据块也是服从正态分布的，并且其均值和方差与所属子数据集的均值和方差近似，这样就可以直接通过分析其中的某部分数据块就能够得出该所属的子数据集所蕴含的信息；如果接近泊松分布，那么通过平均分割该子数据集，从分割得出的数据块中抽取某个数据块进行优化后使之也符合泊松分布，即该数据块的平均值和方差与子数据集的平均值和方差非常近似，这样就可以直接通过分析其中的该数据块就能够得出该所属的子数据集所蕴含的信息。作为优先，大数据集表示为a[1，k]，设定大数据集中的其中某一个数值形式的子数据集为s[a,b]，假设子数据集中的某个数据x∈[a,b],并且满足：其中μ为均值，σ为标准方差，那么可以得出子数据集满足：即可以得出该子数据集是服从正态分布。作为优先，设定子数据集的位置为s(pl,pr),pl和pr均表示位置，且的绝对值小于δ，其中p表示最大数值的位置点，δ表示进行分块时，指针向某数据块集合两边进行调整的最大范围值，以a(p)来表示子数据集s[c-δ,c+δ]中的最大的可能性数值，c＝(pl+pr)/2＝pl+b/2,b＝k/m，c表示子数据集的中间位置，m表示分割的数据块数量，由a(p)∈s，假设s[a,b]满足：a(p)＝max(s),c≈(a+b)/2,|c-p|≤δ，则可以得出s[a,b]为包含一系列服从正态分布的数据块的子数据集，即：其中mr为可动态调整的m参数值，在初始化m值后，随着δ调整分块，m值发生变化，分割过程中剩下的区域由mr来调整，其中xi表示一个左侧相邻区间被动态调整的数据集合内选择的该区间的频率最大值所在的位置值减去此区间左侧相邻的上部区间的位置值。作为优先，所述步骤(3)中描述的正态分布的分割方法为：第二、先设定一些特定的初始化值，即设定整体子数据集为s[1，n]，设定δ表示进行分块时，指针向进行分割的数据块集合两边进行调整的最大范围值，设m表示分割的数据块数量，则b＝n/m表示每个数据块的长度，设lp表示不符合条件的分割点的最大值，设pl为当前进行分割的数据块集合的最左侧位置，设pr为当前进行分割数据块集合的最右侧位置，即pr＝b，设c为当前进行分割的数据块集合的中心位置，即c＝b/2,设cl＝c-δ,cr＝c+δ，即cl表示数据块中心向左移动δ，cr表示数据块中心向右移动δ，设定p＝maxpoint(s,cl,cr，lp)，p表示当前进行分割的该数据块中最接近分割点的点位置，lp表示该数据块中最接近分割点的点的最大值；第二、开始进行分割，从默认第一个数据块开始进行分割，当pr满足pr≤n时，如果|p-c|＞δ，则得出lp＝[lp,p]，p＝maxpoint(s,cl,cr，lp)，即表示确定出该数据块中最接近分割点的点位置，然后在这个点位置附近用cl和cr来做调整找出分割点的位置，在数据块中心向左或向右移动之后确定出分割点，然后再进行分割下一个数据块，需要分割出的数据块的各个参数值为上一个分割得出的数据块调整后的参数值，直到分割出第m个数据块为止。作为优先，所属数值形式的子数据集的数量至少为一列，因为只有增加更多的数字数据才可以提高大数据分析结果的准确性。下列为两个符合正态分布的医疗数据文件，即：1)糖尿病数据源：数据集来自于在美国130所医院和综合交付网络的10年(1999-2008)的临床护理数据集，包括101767条记录,50个数值属性，包括4521条记录。2)健康数据源:这个数据源包含病人信息和他们的在线资源提供的医院记录,该记录患者的婚姻状况、就业状况、住院时间等。我们基于医疗数据来源进行了一系列的实验，这些数据文件是糖尿病数据集和健康数据集。基于两个数据源,实验结果如下:数据集1:μ表示均值，σ表示标准偏差，此数据集是“糖尿病属性”。数据集2:μ表示均值，σ表示标准偏差，此数据集是“健康属性:平衡”。上述两个医疗数据集通过正态分布的分割方法分割后，结果说明如下：为了验证经过正态分布分割方法的数据块的包容性,我们通过分析分割抽样得到的数据块和原始数据集的两个数据源，然后对两者的μ值和σ值进行比较在数据集1中，数据集2被分成15个单独的数据块，我们比较原始数据集的μ和σ值与某个分割数据块相应的μ和σ值，比较表格如下：参数数据集1分割数据块μ486.5324486.552σ212.3062212.1967集合大小1017666784.4分割数据块的μ和σ值非常接近数据集1的μ和σ值，数据集1和分割数据块之间的μ值差为0.0196，分割数据块相对数据集1大约有0.0044％的出入，数据集1和数据集1之间的σ值差异是0.1095，这是分割数据块相对数据集1有约0.516％的变化。在数据集2中，数据集2被分成5个单独的数据块，完整的数据集和某个分割数据块之间的比较在下列表格中列出：分割数据块的μ和σ值非常接近数据集2的μ和σ值，数据集2和分割数据块之间的μ值差为4.48，分割数据块相对数据集2大约有0.0031％的出入，数据集2和分割数据块之间的σ值差异是54.04，这是分割数据块相对数据集2有约0.0719％的变化。所述泊松分布的概率可以表示为：其中k表示在一段时间间隔内某事件发生的频率，λ是在一个时间间隔内平均事件发生的次数，e是欧拉数，k！是k的阶乘，p代表时间发生的概率。对符合泊松分布的数据进行抽样，最终得到的数据块的均值和标准偏差与原始数据集的均值μ和标准偏差σ的对比如下：数据源μσλ原始数据集(1000条数据)100.0288999.09559536790199.441096530586数据块1(2000条数据)99.47694174757399.58713821990199.57710545218数据块2(1250条数据)99.46014605344999.1889026511499.238174168741数据块3(1000条数据)99.50864077669999.27633310395999.314157031216数据块4(625条数据)99.41545667447398.51123650105198.841110280882结果表明,数据块与原始数据集的μ值和σ值非常接近，可以看出，数据块体积越大,结果越好(即与原始数据集相比,更接近σ和值)，当数据块1包括2000条数据时，原始数据集和数据块1之间的相似度比99.45％,当数据块4包括625条数据时，原始数据集和数据块4之间的相似度比99.39％,所以与原始数据集相比，采样得到的数据越大越接近原始数据集信息。大量实验证明了正态分布和泊松分布两种算法在均值(期望)、方差等值上能以平均99％以上的相似度接近原始数据集。当前第1页12