一种脑功能连接分析的Lag‑shift与Granger双约束方法与流程

本发明涉及fmri数据的功能网络连接分析，特别是涉及一种脑功能连接分析的lag-shift与granger双约束方法。

背景技术：

功能磁共振成像(functionalmagneticresonanceimaging，fmri)是一种神经影像学技术，具有高空间分辨率、可重复检测、无创伤性等优点，已成为脑功能研究和脑疾病诊断的重要工具之一。通过利用数据驱动的独立成分分析(independentcomponentanalysis,ica)方法，可以从采集到的全脑fmri数据中提取出被试(subject)在任务态或静息态下的数十个脑空间激活区(spatialmaps)成分及其对应的时间过程(timecourses)成分。空间激活区成分常用于脑功能分析，而时间过程成分可用于脑功能连接(functionalconnectivity)分析，以探究不同脑区之间相互作用与协调的模式，发现脑疾病(如精神分裂症、阿尔兹海默病、抑郁症、躁郁症等)患者与健康对照被试在脑功能连接方面的显著差异，进而用于脑疾病研究与辅助诊断。

功能连接分为无向的功能连接及有向的功能连接。其中，无向的功能连接简称功能连接，强调的是不同脑区之间的相关性。lag-shift算法(见m.j.jafri,g.d.pearlson,m.stevens,andv.d.calhoun,amethodforfunctionalnetworkconnectivityamongspatiallyindependentresting-statecomponentsinschizophrenia,neuroimage39:1666-1681,2008)是一种典型的功能连接方法。该方法逐个计算两个脑区所对应时间过程之间的最大延时相关系数及此时的延时大小，进而研究脑区间的功能连接特性和时间先后关系。

有向的功能连接又称为有效连接(effectiveconnectivity)或因果连接，强调的是两个脑区之间的因果关系。格兰杰因果分析(grangercausalityanalysis)，简称granger，是一种常用的有效连接分析方法。granger方法采用的是多元自回归模型，根据两个时间序列的过去值对现在值的预测结果，判断两者之间的granger因果关系(见c.w.j.granger,investigatingcausalrelationsbyeconometricmodelsandcross-spectralmethods,econometrica37(3):424-4381969)。假设xt和yt为两个零均值的平稳时间序列，那么因果模型可以表示为

其中，ap，bp，cp和dp为自回归参数，εt和ηt是两个零均值不相关的白噪声序列，e[εt]＝0，e[ηt]＝0，且

xt和yt使用其过去的m个值进行预测，m也可以理解为自回归模型的阶数。如果使用了时间序列yt的过去值yt-j,j＝1,…,m去预测时间序列xt，比仅仅使用xt的过去值xt-j,j＝1,…,m去预测时间序列xt的噪声方差更小，则可以说yt是xt的granger原因；反之亦然。

在现有脑功能连接分析中，无论是针对相同的fmri数据(如静息态数据)还是不同的fmri数据(如运动、视觉、听觉等任务态数据)，各种方法的分析大多彼此独立。换句话说，要么采用lag-shift算法进行功能连接分析，要么采用granger进行因果分析，目前尚未见到二者的联合分析。这样一来，不同方法的分析结果也相互独立，难于比较，而且，每种方法所检测结果的鲁棒性和稳定性也缺乏依据。而对于同一种fmri数据，不同分析方法检测的脑功能连接，应该既有区别又有联系。因此，开发不同分析方法之间的内在联系，提取鲁棒而稳定的脑功能连接，对深入推进脑功能研究和脑疾病诊断极为重要。

技术实现要素：

本发明的目的在于，提供一种对fmri数据联合进行lag-shift功能连接分析与granger因果连接分析的方法，揭示两种方法检测结果之间的内在联系，提取稳定的脑网络连接。

本发明的技术方案是，对于从多被试fmri数据中提取的时间过程(timecourse,tc)成分，同时进行lag-shift功能连接分析与granger因果连接分析。通过对lag-shift功能连接分析方法施加延时约束，以及对granger因果连接分析方法施加因果一致性(causalitycoherence)约束，因果一致性也就是因果性强度，寻找功能连接与有效连接的内在一致性，提取两种方法共有的网络连接，作为多被试fmri数据的稳定脑功能连接加以输出。具体步骤如下：

第一步，输入从k个被试fmri数据中分别提取的tc成分，记为x^′(k)∈r^l×t,k＝1,…,k，l为tc成分的个数，t为tc成分的时间点数；

第二步，采用截止频率为fl～fh(单位hz)的带通滤波器对x^′(k)进行滤波，得到滤波后的时间过程成分x^(k)∈r^l×t，k＝1,…,k；fl～fh可根据tc成分的频率特性进行选择，对于静息态fmri数据，可选为0.015～0.15(单位hz)；

第三步，对于lag-shift功能连接分析方法，逐个被试计算：令k＝1；

第四步，令延时范围为[-t,+t]，以循环移位方式计算第k个被试数据x^′(k)中每两个tc成分间的最大延时相关及其对应延时i,j＝1,…,l，i≠j。令tc成分i与成分j的时间序列用xt与yt表示，那么lag-shift计算方法如下：

其中，ρδt表示时间序列xt与yt在延时为δt下的延时相关大小。在计算出延时范围[-t,+t]内不同δt取值下延时相关系数后，lag-shift算法选择其中最大的延时相关系数并将此时对应的延时大小记录为延时范围[-t,+t]可根据实际fmri数据进行设定，对于静息态fmri数据，可设置为[-3s,+3s]；

第五步，判断k是否小于k，若是，则k＝k+1，并跳转到第四步；若否，则跳转到第六步；

第六步，剔除非显著连接，保留显著连接：对于k个被试的各个相同连接的i,j＝1,…,l，i≠j，例如分别利用单样本t检验计算t值，保留p<0.05即t>tth的显著性连接，剔除其他连接；tth是在自由度为k-1的情况下，p<0.05所对应的t值，可查表得到。例如，k＝82时，tth＝1.99；

第七步，对于显著连接，计算k个被试的各相关系数与时延的平均值，记为与

第八步，约束时延：挑选出延时的连接，剔除的连接；δ′可根据对的约束强度进行设置，约束强度越大，δ′越大；

第九步，对于granger因果连接分析方法，逐个被试计算：令k＝1；

第十步，计算第k个被试数据x^′(k)中每两个tc成分间的因果一致性和i,j＝1,…,l，i≠j。根据公式(1)(2)(3)(4)，若tc成分i与成分j的时间序列用xt与yt表示，那么：

式中，

第十一步，判断k是否小于k，若是，则k＝k+1，并跳转到第十步；若否，则跳转到第十二步；

第十二步，剔除非显著连接，保留显著连接：对于k个被试的各个相同连接的因果一致性参数和i,j＝1,…,l，i≠j，例如分别利用单样本t检验计算t值，保留p<0.05即t>tth的显著性连接，剔除其他连接；tth的意义同第六步介绍；

第十三步，对于显著连接，计算k个被试的各因果一致性的平均值，记为和

第十四步，约束因果一致性差值：挑选出的连接，剔除的连接；c′可根据对的约束强度进行设置，约束强度越大，c′越大；

第十五步，对于上述lag-shift功能连接分析与granger因果分析得到的连接结果，参见第八步和第十四步结果，检测两种方法的相同连接；

第十六步，输出两种方法的相同连接，作为稳定连接。

本发明所达到的效果和益处是，通过利用双约束联合分析方法，建立lag-shift功能连接分析方法与granger有效连接分析方法之间的桥梁，提取稳定而鲁棒的脑功能连接，为基于fmri数据的脑功能研究和脑疾病诊断提供更好的技术支持。例如，以默认网络(defaultmodenetwork,dmn)内部7个子成分为对象(见图2-图5)，以本发明提取的稳定连接(见图3、图5)为目标网络，采用granger有效连接分析方法对40个健康被试对照组与42个精神分裂症患者组进行有效连接分析，结果表明，精神分裂症患者组与健康对照组在目标网络的连接结果上存在显著差异，可用于精神分裂症分类。

附图说明

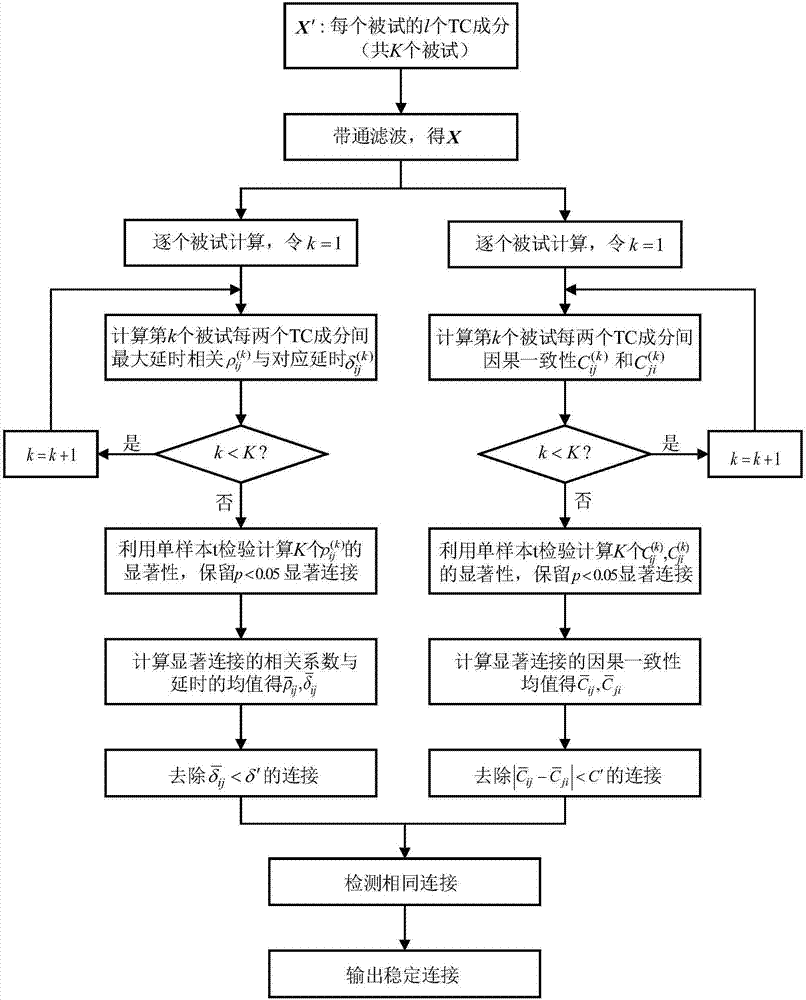
图1是本发明的流程图；

图2是对82个被试静息态fmri数据7个dmn子网络进行lag-shift分析所得的显著连接结果图；

图3是对lag-shift的显著连接结果施加延时约束后得到的功能连接图；

图4是对82个被试静息态fmri数据7个dmn子网络进行granger分析所得的显著连接结果图；

图5是对granger的显著连接结果施加因果一致性差值约束后得到的有效连接图。

具体实施方式

下面结合技术方案和附图，详细叙述本发明的一个具体实施例。

现有82个被试(k＝82)的静息态fmri数据，利用gift工具箱(http://mialab.mrn.org/software/gift/index.html)提供的groupica方法(v.calhoun,t.adali,g.pearlson,andj.pekar,amethodformakinggroupinferencesfromfunctionalmridatausingindependentcomponentanalysis,humanbrainmapping14:140-151,2001)，采用infomax算法分离得到120个脑空间激活区成分及其对应的tc成分。根据smith脑空间激活区参考模板(s.m.smith,p.t.fox,k.l.miller,d.c.glahn,p.m.fox,c.e.mackay,etal.,correspondenceofthebrain’sfunctionalarchitectureduringactivationandrest,proceedingsofthenationalacademyofsciences106(31):13040-13045,2009)，按照相关最大化原则挑选出dmn的l＝7个感兴趣子网络，提取其对应于每个被试的7个tc成分，每个tc成分的时间点数t＝150。实施本发明的具体步骤如下(见图1)：

第一步，输入从82个被试fmri数据中分别提取的7个tc成分，记为x^′(k)∈r^7×150,k＝1,…,82；

第二步，采用截止频率为0.015～0.15(单位hz)的带通滤波器对x^′(k)进行滤波，得到滤波后的时间过程成分x^(k)∈r^7×150,k＝1,…,82；

第三步，对于lag-shift功能连接分析方法，逐个被试计算：令k＝1；

第四步，令延时范围为[-3s,+3s]，利用公式(5)，以循环移位方式计算第k个被试数据x^′(k)中每两个tc成分间的最大延时相关及其对应延时i,j＝1,…,7，i≠j。

第五步，判断k是否小于82，若是，则k＝k+1，并跳转到第四步；若否，则跳转到第六步；

第六步，剔除非显著连接，保留显著连接：对于82个被试的各个相同连接的分别利用单样本t检验计算t值，保留p<0.05即t>1.99的显著性连接，剔除其他连接，结果如图2所示；

第七步，对于显著连接，计算82个被试的相关系数与时延的平均值，记为与

第八步，约束时延：挑选出延时的连接，剔除的连接，结果如图3所示；

第九步，对于granger因果连接分析方法，逐个被试计算：令k＝1；

第十步，利用公式(6)(7)，计算第k个被试数据x′^(k)中每两个tc成分间的因果一致性和i,j＝1,…,7，i≠j；

第十一步，判断k是否小于82，若是，则k＝k+1，并跳转到第十步；若否，则跳转到第十二步；

第十二步，剔除非显著连接，保留显著连接：对于k个被试的各个相同连接的因果一致性参数和i,j＝1,…,7，i≠j，分别利用单样本t检验计算t值，保留p<0.05即t>1.99的显著性连接，剔除其他连接，结果如图4所示；

第十三步，对于显著连接，计算82个被试的因果一致性的平均值，记为和

第十四步，约束因果一致性差值：挑选出的连接，剔除的连接，结果如图5所示；

第十五步，对于上述lag-shift功能连接分析与granger因果分析得到的连接结果，参见图3和图5的结果，检测两种方法的相同连接；

第十六步，输出两种方法的相同连接，即图3和图5中的连接，作为稳定连接。