一种基于结构特征描述的三维几何模型去噪方法与流程

本发明涉及一种基于结构特征描述的三维几何模型去噪方法。

背景技术：

随着数字化扫描技术的普及，获取大规模测量点所重建的三维几何模型已经被越来越多的领域广泛应用，如影视娱乐、虚拟现实、医疗诊断、工业制造、文物保护等。由于数字化设备精度误差、三维重建方法缺陷及一些人为因素等，获得的模型不可避免地存在各种噪声和扰动，它们的存在十分不利于显示传输及其他后续几何处理和分析操作，如几何模型参数化、三维水印、网格变形等，因此需要对获取的几何模型进行去噪处理。

几何模型去噪早期的工作主要有基于拉普拉斯的光顺、基于曲率流的扩散以及基于频率域的滤波等方法。这些方法虽然能够很好的去除模型的噪声，但是由于在去噪过程中未将特征和噪声进行区分，很容易产生过光顺而将几何模型的一些特征去除。为了在剔除几何模型噪声的同时保持固有的几何特征，本领域技术人员提出了一些能够保持几何模型特征的各向异性的平滑方法，诸如基于双边滤波的去噪、基于各向异性扩散的光顺算法、基于全变分优化的去噪、基于压缩感知的去噪等。然而，现有的局部迭代的几何模型去噪方法一般不能保证结果的收敛性，比较容易出现几何模型体积收缩现象，整体优化的去噪方法通常需要将原始模型信息作为约束，容易将噪声看作特征而不能很好的去噪，而且对于大规模几何模型的处理速度较慢。

技术实现要素：

本发明的目的是为了降低噪声的同时保持输入几何模型的尖锐特征，提供一种基于结构特征描述的三维几何模型去噪方法，它从几何信号的角度出发，构建一种有效的几何结构特征描述子，并将其融入在非局部均值滤波框架中进行几何模型去噪，防止几何模型的体积收缩，提高去噪的有效性和鲁棒性。

本发明的目的是通过以下技术方案来实现的：一种基于结构特征描述的三维几何模型去噪方法，其特征是，它包括以下步骤：

1)几何信号的构建

对于以三角网格表示的三维几何模型，通过几何模型顶点的拉普拉斯算子和顶点法向进行内积构建几何信号，该信号能够刻画几何模型的局部细节特征；

2)基于法向张量的结构特征描述子的计算

通过顶点法向张量的所有特征值的和以及最小单位特征向量作为结构特征测度描述子，该描述子能够刻画几何模型上角点、边点和面点的特征信息；

3)几何信号的非局部均值滤波

通过各顶点相互之间结构特征测度描述子的差异作为非局部均值滤波的权值计算依据，对顶点的离散拉普拉斯算子与对应顶点法向量内积所得的几何模型上信号进行非局部均值滤波，得到一个新的几何信号；

4)几何模型重建

将原始几何模型顶点作为约束条件，通过将步骤3)所得的滤波后新的几何信号进行拉普拉斯曲面重建，得到非局部均值滤波后信号对应的几何模型；

所述步骤1)中几何信号的构造的具体实现为：

设{vi|i＝1,2,…,n}为以三角网格表示的三维几何模型的n个顶点，δ(vi)为顶点vi的离散拉普拉斯算子，顶点法向量为ni，将几何信号定义为两者内积形式为(1)式：

si＝(δ(vi),ni)(1)

对于几何模型上所有顶点的几何信号，可以写成(2)式的矩阵形式：

lv＝sn(2)

其中v表示几何模型顶点的位置向量矩阵，s＝diag(s1,s2,…,sn)表示以顶点信号si作为对角线元素的矩阵，n为顶点的法向矩阵，l为几何模型的拉普拉斯矩阵，具有(3)式形式：

其中wij＝cotαij+cotβij，αij,βij是顶点vi与vj连线所成的边所对的两个角，n(i)是顶点vi的一环邻域点集。

所述步骤2)中基于法向张量的结构特征描述子的计算具体实现为：

对于给定的几何模型顶点vi，其法向张量可由它周围的三角面片的单位法向量定义为(4)式：

其中f(vi)表示顶点vi周围的三角形的指标集合，为(5)式的权重系数：

a(fk)是三角形fk的面积，amax是顶点vi周围的三角形的最大面积，是三角形fk重心；

由于法向张量为三阶对称半正定矩阵，可以求出其特征值λ1≥λ2≥λ3≥0和所对应的单位特征向量e1,e2,e3，由于几何模型上角点、边点和面点所对应的特征值有明显的差距，而且最小特征向量的方向e3对应着顶点的特征方向，采用(6)式的度量作为顶点结构特征测度描述子：

des(vi)＝{di,ti}(6)

其中di＝λ1+λ2+λ3，ti对应顶点法向张量的最小特征向量；

在此基础上，通过(7)式如下度量来计算各顶点之间结构特征描述子的差异：

d(vi,vj)＝(di-dj)²+(1-|(tj,ti)|)(7)

其中(tj,ti)表示顶点特征方向的内积，该差异值越小，说明两个顶点的结构特征越相似。

所述步骤3)中几何信号的非局部均值滤波的具体实现为：

将步骤2)中定义的结构特征测度描述子作为非局部均值滤波权值的计算依据，对步骤1)中构造的几何信号si进行非局部均值滤波得到一个新的几何信号s′i，计算式为(8)式：

其中nσ(i)是顶点vi以σ为半径的邻域点集，σ为几何模型平均边长的β∈[1.5,3]倍，权重系数wij通过各顶点之间结构特征测度描述子进行计算，即为式(9)-(10)式：

h表示几何模型去噪的强度，可取为h∈[0.05,0.35]。

所述步骤4)中几何模型重建的具体实现为：

通过将滤波后新的信号s′i进行最小二乘求解得到新的几何模型顶点v′，即最小化为(11)式表示的能量：

该能量可以改写为(12)式：

其可以转化为一个2n×n的线性方程组(13)式：

其中s′＝diag(s′1,s′2,…,s′n)表示以步骤3)中所得的顶点信号s′i作为对角线元素的矩阵，n为几何模型顶点的个数，l为原始几何模型的拉普拉斯矩阵，in×n为n阶单位矩阵，n为原始几何模型顶点的法向矩阵，v为原始几何模型顶点的位置向量矩阵，μ为顶点约束的权重因子，边界顶点的约束权值为1，内部顶点的约束权值为0.1。

本发明的优点体现在：

1.本发明提出的基于法向张量的结构特征描述子不仅考虑模型上单点的几何量，还考虑整体特征方向的一致性，对有尖锐特征的cad模型和具有细节特征的非cad模型的特征均能较好的刻画，具有较好的鲁棒性；

2.本发明通过引入原始几何模型顶点作为约束对于滤波后信号进行拉普拉斯模型重建，能够在几何模型平滑过程中阻止边界和体积收缩；

3.本发明从几何信号的角度出发，将非局部均值滤波引入到拉普拉斯几何处理框架中，具有较高执行效率和很好的普适性。

附图说明

图1是本发明的一种基于结构特征描述的三维几何模型去噪方法的流程图；

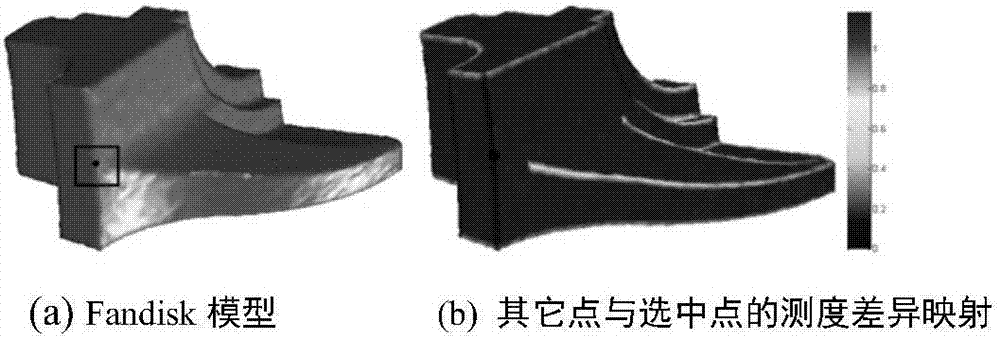
图2是本发明具体实施中基于法向张量的结构特征测度描述的差异映射示意图；

图3是本发明具体实施中对几何信号进行非局部均值滤波前后对比示意图；

图4为本发明具体实施中对octahedron模型的去噪结果示意图；

图5为本发明具体实施中对fandisk模型的去噪结果示意图；

图6为本发明具体实施中对mannequin模型的去噪结果示意图；

图7为本发明具体实施中对julius模型的去噪结果示意图；

图8为本发明具体实施中对angle模型的去噪结果示意图；

图9为本发明具体实施中对moai模型的去噪结果示意图。

具体实施方式

下面利用附图和实例对本发明作进一步说明。

参照图1，本发明的一种基于结构特征描述的三维几何模型去噪方法，包括以下步骤：

1)几何信号的构建

读入带有噪声的几何模型，对具有尖锐特征的cad模型和具有细节特征的非cad模型均适用；对于以三角网格表示的三维几何模型，通过几何模型顶点的拉普拉斯算子和顶点法向进行内积构造几何信号，该信号能够刻画几何模型的局部细节特征；

所述步骤1)中几何信号的构造的具体实现为：

设{vi|i＝1,2,…,n}为以三角网格表示的三维几何模型的n个顶点，δ(vi)为顶点vi的离散拉普拉斯算子，顶点法向量为ni，将几何信号定义为两者内积形式为(1)式：

si＝(δ(vi),ni)(1)

对于几何模型上所有顶点的几何信号，可以写成(2)式的矩阵形式：

lv＝sn(2)

其中v表示几何模型顶点的位置向量矩阵，s＝diag(s1,s2,…,sn)表示以顶点信号si作为对角线元素的矩阵，n为顶点的法向矩阵，l为几何模型的拉普拉斯矩阵，具有(3)式形式：

其中wij＝cotαij+cotβij，αij,βij是顶点vi与vj连线所成的边所对的两个角，n(i)是顶点vi的一环邻域点集。

2)基于法向张量的结构特征描述子的计算

通过顶点法向张量的所有特征值的和以及最小单位特征向量作为结构特征测度描述子，该描述子能够刻画几何模型上角点、边点和面点的特征信息；

基于法向张量的结构特征描述子的计算具体实现为：

对于给定的几何模型顶点vi，其法向张量可由它周围的三角面片的单位法向量定义为(4)式：

其中f(vi)表示顶点vi周围的三角形的指标集合，为(5)式的权重系数：

a(fk)是三角形fk的面积，amax是顶点vi周围的三角形的最大面积，cfk是三角形fk重心，

由于法向张量为三阶对称半正定矩阵，可以求出其特征值λ1≥λ2≥λ3≥0和所对应的单位特征向量e1,e2,e3，由于几何模型上角点、边点和面点所对应的特征值有明显的差距，而且最小特征向量的方向e3对应着顶点的特征方向，采用(6)式的度量作为顶点结构特征测度描述子：

des(vi)＝{di,ti}(6)

其中di＝λ1+λ2+λ3，ti对应顶点法向张量的最小特征向量；

在此基础上，通过(7)式如下度量来计算各顶点之间结构特征描述子的差异：

d(vi,vj)＝(di-dj)²+(1-|(tj,ti)|)(7)

其中(tj,ti)表示顶点特征方向的内积，该差异值越小，说明两个顶点的结构特征越相似。

图2给出了在带有噪声的fandisk几何模型的竖直方向的尖锐特征边上选定一个顶点后，通过本发明提出的基于法向张量的结构特征测度描述方法对顶点进行描述时的差异映射示意图。从中可以看到，竖直方向特征边上的顶点与选定的顶点的相似性非常接近，说明该描述子能较好的描述具有相同结构特征的顶点的相似性，能够有效地应用到非局部均值滤波的去噪框架中。

3)几何信号的非局部均值滤波

通过各顶点相互之间结构特征测度描述子的差异作为非局部均值滤波的权值计算依据，对顶点的离散拉普拉斯算子与对应顶点法向量内积所得的几何模型上信号进行非局部均值滤波，得到一个新的几何信号；图3给出了非局部均值滤波前后信号对比示意图。

几何信号的非局部均值滤波的具体实现为：

将步骤2)中定义的结构特征测度描述子作为非局部均值滤波权值的计算依据，对步骤1)中构建的几何信号si进行非局部均值滤波得到一个新的几何信号s′i，计算式为(8)式：

其中nσ(i)是顶点vi以σ为半径的邻域点集，σ为几何模型平均边长的β∈[1.5,3]倍，权重系数wij通过各顶点之间结构特征测度描述子进行计算，即为式(9)-(10)式：

h表示几何模型去噪的强度，可取为h∈[0.05,0.35]。

4)几何模型重建

将原始几何模型顶点作为约束条件，通过将步骤3)所得的滤波后新的几何信号进行拉普拉斯曲面重建，得到非局部均值滤波后信号对应的几何模型。

几何模型重建的具体实现为：

通过将滤波后新的信号s′i进行最小二乘求解得到新的几何模型顶点v′，即最小化为(11)式表示的能量：

该能量可以改写为(12)式：

其可以转化为一个2n×n的线性方程组(13)式：

其中s′＝diag(s′1,s′2,…,s′n)表示以步骤3)中所得的顶点信号s′i作为对角线元素的矩阵，n为几何模型顶点的个数，l为原始几何模型的拉普拉斯矩阵，in×n为n阶单位矩阵，n为原始几何模型顶点的法向矩阵，v为原始几何模型顶点的位置向量矩阵，μ为顶点约束的权重因子，边界顶点的约束权值为1，内部顶点的约束权值为0.1。

图4和图5给出了针对具有尖锐特征的cad模型加入高斯噪声后的去噪结果；图6和图7给出了对具有细节特征的非cad模型加入高斯噪声后的去噪结果；图8和图9给出了含有真实噪声的模型数据的去噪结果。

本发明的具体实施方式并非穷举，本领域技术人员不经过创造性劳动的简单复制和改进，应属于本发明专利要求的保护范围。