一种基于Rendezvous哈希算法的虚拟机初始放置策略方法与流程

本发明涉及到一种基于rendezvous哈希算法的虚拟机初始放置策略方法。

背景技术：

云计算是最近几年备受业界关注的新热点，而虚拟化技术是实现云计算的重要手段。通过虚拟化技术,云数据中心借虚拟机共享物理机资源池的方式，以物理机单元承载虚拟机，以虚拟机单元承载应用服务。云数据中心已经成为一个高性能计算机的集合，具有成千上万的物理服务器和网络设备。由于资源量大、异构性强，云数据中心对按需服务、资源动态弹性管理、服务质量等多方面的要求更加突出。但是，云数据中心现在面临着低效率、高成本、高能耗等问题。

资料表明：我国的云数据中心的资源利用率普遍不高，平均只有10％左右，而且服务器在较大一部分时间内处于空闲状态，即使服务器处于空闲状态，也会带来满负荷时60％的功耗。因此，如何合理的利用资源，提高资源利用率，减低能源的消耗是当前云数据中心面临的主要问题。如何合理的进行虚拟机放置也已经成为降低数据中心能耗的一大研究热点。

虚拟机的初始化放置管理是研究如何在一个没有负载的云数据中心、根据虚拟化的类型和对资源的请求选择合适的目的物理机的过程，类似于装箱问题的np-hard问题。初始化放置具有长期性，对数据中心资源的有效利用，能耗节约起重要作用。以此来降低数据中心初始能耗，并且实现数据中心中主机的负载均衡。

在虚拟机对应主机的初始化放置问题的研究中，大多数学者采用启发式算法如优先适应、或降序最佳适应等贪婪算法来搜索虚拟机放置的最优解。beloglazov以及buyya等人在2010年提出一种基于cpu利用率的降序最佳适应算法。malani，amdani等人在2015年提出了一种基于内存利用率的蚁群算法，panigraphy、talwar等人在2011年提出一种综合考虑cpu和内存两种负载类型的基于ffd的启发式算法。

综上所述，启发式算法基本是单点搜索，无法综合考虑数据中心能耗以及负载均衡两方面；智能算法仅考虑单维因素，且当参与调度的虚拟机以及主机数量较大时容易陷入局部最优解的情况。因此，本专利提出一种基于rendezvous哈希算法的虚拟机初始化策略来实现负载均衡，并且综合考虑cpu、内存因素，达到数据中心能耗降低，提高主机cpu、内存利用率的目标。

技术实现要素：

为了克服现有的虚拟机放置策略的负载不均衡、没有综合考虑cpu、内存因素的不足，本发明提出一种基于rendezvous哈希算法的虚拟机放置策略方法，适用于云计算环境下，虚拟机到主机的物理资源调度的初始放置，建立虚拟机到主机的映射关系，整个策略综合考虑负载均衡、虚拟机主机性能、数据中心能耗等因素，最终实现物理资源的合理调度。

本发明所采用的技术方案是：

一种基于rendezvous哈希算法的虚拟机放置策略方法，包括以下步骤：

第一步：首先定义数据中心存在的物理主机集合pm＝{pm1,pm2,…,pmn}，其中主机数量为n，需要初始化放置的虚拟机集合vm＝{vm1,vm2,…,vmm}，其中虚拟机数量为m，设定虚拟机数量m大于或等于主机n；

第二步：对于给定的虚拟机vmi，定义vpesi为虚拟机vmi所需的cpu资源，vrami为虚拟机vmi所需的内存资源，vi-pes为虚拟机vmi的cpu利用率，wi-ram为虚拟机vmi的内存利用率。对于给定的主机pmj，定义ppesj为主机pmj当前的cpu空闲资源，pramj为主机pmj的内存空闲资源，uj-pes为主机pmj的cpu利用率，uj-ram为主机pmj的内存利用率，则定义主机pmj的资源利用率uj为：

uj＝α*uj-pes+β*uj-ram

其中0<α<1,0<β<1，且α+β＝1。

定义tagij为当前时刻，主机pmj能否满足虚拟机vmi的资源要求，即

tagij＝(ppesj-vpesi)>0∧(pramj-vrami)>0

第三步：给定主机pmj，定义该主机在t时刻的电源能耗表示为：

ej(t)＝cj+k*fj³(t)*uj(t)

其中cj为静态能耗标记，fj(t)为t时刻主机pmj的频率，uj(t)为t时刻主机pmj的功率(watt)，k为线性常量；

则在t时间内，主机pmj的能耗ej：

第四步：由于构建和维护虚拟分层结构需要一定的系统开销，主机数量n小于4，即无法满足构建最小双层虚拟结构的数量2*2时，则对于任意虚拟机vmi，定义其对应每个主机具有一个分配权重得分集合wi＝{wi1，wi2，…，wik}，其中k≥n；定义wij为虚拟机vmi在主机pmj上的权重得分，wij＝h(vmi,pmj)，其中h()内包含约定的哈希函数；然后直接通过rendezvous哈希算法将虚拟机vmi分配给权重wij最大的主机pmj；如果主机pmk的性能是其他主机的h倍，则简单的表示pmkh次；

第五步：主机数量n大于等于4，即满足构建最小双层虚拟结构的数量时，建立虚拟分层结构，虚拟分层结构包含虚拟分层节点和真实主机节点簇两部分，虚拟分层节点之间以树的形式分布，其中，将虚拟分层节点的所有叶子节点称为虚拟叶子节点扇区，虚拟分层节点构成的树的高度称为虚拟分层结构深度；真实主机节点簇是由多个真实主机构成的集合，与虚拟分层节点底部虚拟叶子节点相关联。

进一步，所述虚拟机放置策略方法还包括以下步骤：

第六步、出现各种人为或自然原因导致物理主机宕机或删除、或者由于计算需求增大需要增加物理主机的情况。处理过程如下：：

6.1、对于给定虚拟机，若最终选择的真实主机节点资源不够分配导致不可用或已经宕机，选择权重值略高的同一簇中的真实主机节点完成分配；

6.2、对于给定虚拟机，若最终选择的真实主机节点资源不够分配导致不可用或已经宕机，且同簇下无法找到可用的真实主机节点进行分配，这种情况下，可以在虚拟分层结构中往上上升一个或多个层级，并从该层的同级虚拟节点中选择一个作为代替，再次将该层级降级到真实节点簇，寻找可用的真实主机节点；

6.3、当最后的主机簇还未满z时，直接将主机加入至该主机簇中；

6.4、当最后的主机簇的节点数为z时，且虚拟分层结构最底层未满时，增加一个主机簇；

6.5、当最后的主机簇的节点数为z时，且虚拟分层结构最底层也满时，将该主机增加至第一个主机簇，这时，主机簇的常量z＝z+1。

再进一步，所述第五步中，建立虚拟分层结构的过程如下：

5.1主机簇群划分，首先选择一个常数z，将主机集合按照c＝ceiling(n/z)组织成簇，其中ceiling函数表示将n除以z的值向上舍入为最接近的整数，c0＝{cpm1，cpm2，…，cpmz}，c1＝{cpmz+1，cpmz+2，…，cpm2z}，…直至每个主机都归属于一个簇。每个簇为虚拟分层结构中的最底层节点；

5.2虚拟叶子节点扇区以及虚拟分层结构深度确定，选择虚拟分层结构中每个子节点扇区的叶子数f，即从根节点出发，每个节点有f个子虚拟节点；根据节点扇区的叶子数f以及主机簇个数c，得到虚拟分层结构的深度h：

f^h≥c

其中h是最小正整数，使得上述公式成立；

5.3各虚拟叶子节点扇区编号。一般采用自然编号对每个扇区分别统一编号，例如从0，1，2，…，f-1；

5.4对于某一虚拟机vmi，对于任意一个虚拟节点s，都有一个对应的权重wis＝h(vmi,s)，在虚拟分层结构的每一层叶子扇区，都可通过rendezvous哈希算法计算各虚拟节点权重，选择得分最高的节点继续向下分层，直到选择至最底层的真实主机节点簇cl；

5.5当虚拟机vmi选中真实主机节点簇cl后，在进行真实节点选择时，假设对于任意在真实节点簇cl中的主机节点cpmlz+j，都有一个对应的权重得分wi(lz+j)＝h(vmi,cpmlz+j)*tagi(lz+j)，若tag为false,则为0,若为true默认为1；其中，将虚拟机vmi分配给主机cpmlz+j之后，h(vmi,cpmlz+j)为在相同t时间段内，eold与分配虚拟机vmi后的真实主机节点簇cl的总体能耗的比值，以及主机pmlz+j的资源利用率ulz+j与1的差方和对应权重常数的乘积的和：

其中ei+lz为t时间段内主机cpmlz+j的能耗，eold是指相同t时间段内，未分配新虚拟机时，真实主机节点簇cl的能耗。γ、δ是表示两者的权重；

因此，虚拟机vmi最终会选择使权重得分wi(lz+j)最高的主机节点完成分配。

更进一步，在虚拟分层结构中，虚拟节点的选择从任意层级进行，若从根节点开始选择，则直到选择到真实主机节点的过程中，一共需要的哈希值数量为count＝f*h次，其中f为每个子节点扇区的叶子数，h为虚拟分层结构的。

本发明的技术构思为：云计算环境下虚拟机初始化放置策略繁多，现存大多方法未综合考虑物理资源调度的负载均衡度，使单一主机负载过重以及物理主机的动态增加、删减给数据中心带来的能耗问题。本发明基于rendezvous哈希算法思想，构建虚拟分层结构实现虚拟机至主机的负载均衡分配。对于每个虚拟机，通过rendezvous哈希算法，都会给定一个对应各虚拟节点的权重得分，选择得分较高的虚拟节点进行选择。通过对主机进行簇的划分，并将簇作为虚拟分层结构的最底层节点，使得主机宕机或故障时的动态删除以及动态增加时产生的能耗和代价最低。在虚拟机对主机节点进行的选择过程中，综合考虑真实主机节点簇的整体能耗，选择是真实主机节点簇能耗最低的分配方案，来达到数据中心全局能耗降低的效果。

本发明的有益效果主要表现在要：(1)使用虚拟分层结构以及rendezvous哈希算法选择虚拟节点，可以实现虚拟机到主机物理资源调度的负载均衡。(2)算法复杂度为o(logn)，效率相对较高。(3)选择主机节点时，采用选择真实主机簇局部能耗最低的方案，有效降低数据中心的总体能耗。(4)当主机宕机或需要增加或删除时，则只有映射到该主机的对象被重新映射到其他主机，可以最大程度不影响原始虚拟机主机映射关系。

附图说明

图1示出了基于rendezvous哈希算法的虚拟机初始放置策略流程图。

图2示出了虚拟分层结构图。

图3示出了虚拟分层结构进行虚拟机分配步骤图。

具体实施方式

下面结合附图对本发明作进一步描述。

参照图1～图3，一种基于rendezvous哈希算法的虚拟机初始放置策略方法，包括以下步骤：

第一步：首先定义数据中心存在的物理主机集合pm＝{pm1,pm2,…,pmn}，其中主机数量为n，需要初始化放置的虚拟机集合vm＝{vm1,vm2,…,vmm}，其中虚拟机数量为m，设定虚拟机数量m大于或等于主机n；

第二步：对于给定的虚拟机vmi，定义vpesi为虚拟机vmi所需的cpu资源，vrami为虚拟机vmi所需的内存资源，vi-pes为虚拟机vmi的cpu利用率，wi-ram为虚拟机vmi的内存利用率，对于给定的主机pmj，定义ppesj为主机pmj当前的cpu空闲资源，pramj为主机pmj的内存空闲资源，uj-pes为主机pmj的cpu利用率，uj-ram为主机pmj的内存利用率，则定义主机pmj的资源利用率uj为：

uj＝α*uj-pes+β*uj-ram

其中0<α<1,0<β<1，且α+β＝1；

定义tagij为当前时刻，主机pmj能否满足虚拟机vmi的资源要求，即

tagij＝(ppesj-vpesi)>0∧(pramj-vrami)>0

第三步：给定主机pmj，定义该主机在t时刻的电源能耗表示为：

ej(t)＝cj+k*fj³(t)*uj(t)

其中cj为静态能耗标记，fj(t)为t时刻主机pmj的频率，uj(t)为t时刻主机pmj的功率(watt)，k为线性常量；

则在t时间内，主机pmj的能耗ej：

第四步：由于构建和维护虚拟分层结构需要一定的系统开销，主机数量n小于4，即无法满足构建最小双层虚拟结构的数量2*2时，，则对于任意虚拟机vmi，定义其对应每个主机具有一个分配权重得分集合wi＝{wi1，wi2，…，wik}，其中k≥n；定义wij为虚拟机vmi在主机pmj上的权重得分，wij＝h(vmi,pmj)，其中h()内包含约定的哈希函数；然后直接通过rendezvous哈希算法将虚拟机vmi分配给权重wij最大的主机pmj；如果主机pmk的性能是其他主机的h倍，则简单的表示pmkh次；

第五步：主机数量n大于等于4，即满足构建最小双层虚拟结构的数量时，建立虚拟分层结构，虚拟分层结构包含虚拟分层节点和真实主机节点簇两部分，虚拟分层节点之间以树的形式分布，其中，将虚拟分层节点的所有叶子节点称为虚拟叶子节点扇区，虚拟分层节点构成的树的高度称为虚拟分层结构深度；真实主机节点簇是由多个真实主机构成的集合，与虚拟分层节点底部虚拟叶子节点相关联。

第六步、出现各种人为或自然原因导致物理主机宕机或删除、或者由于计算需求增大需要增加物理主机的情况，处理过程如下：：

6.1、对于给定虚拟机，若最终选择的真实主机节点资源不够分配导致不可用或已经宕机，选择权重值略高的同一簇中的真实主机节点完成分配；

6.2、对于给定虚拟机，若最终选择的真实主机节点资源不够分配导致不可用或已经宕机，且同簇下无法找到可用的真实主机节点进行分配，这种情况下，可以在虚拟分层结构中往上上升一个或多个层级，并从该层的同级虚拟节点中选择一个作为代替，再次将该层级降级到真实节点簇，寻找可用的真实主机节点；

6.3、当最后的主机簇还未满z时，直接将主机加入至该主机簇中；

6.4、当最后的主机簇的节点数为z时，且虚拟分层结构最底层未满时，增加一个主机簇；

6.5、当最后的主机簇的节点数为z时，且虚拟分层结构最底层也满时，将该主机增加至第一个主机簇，这时，主机簇的常量z＝z+1。

图1为本发明基于rendezvous哈希算法的虚拟机初始放置策略流程图。具体策略步骤如下：

1.1首先定义数据中心存在的物理主机集合pm＝{pm1,pm2,…,pmn}，其中主机数量为n，需要初始化放置的虚拟机集合vm＝{vm1,vm2,…,vmm}，其中虚拟机数量为m。(假设虚拟机数量m大于或等于主机n)。

1.2对于给定的虚拟机vmi，定义vpesi为虚拟机vmi所需的cpu资源，vrami为虚拟机vmi所需的内存资源，vi-pes为虚拟机vmi的cpu利用率，wi-ram为虚拟机vmi的内存利用率。对于给定的主机pmj，定义ppesj为主机pmj当前的cpu空闲资源，pramj为主机pmj的内存空闲资源，uj-pes为主机pmj的cpu利用率，uj-ram为主机pmj的内存利用率，则定义主机pmj的资源利用率为：

uj＝α*uj-pes+β*uj-ram

其中0<α<1,0<β<1，且α+β＝1。

定义tagij为当前时刻，主机pmj能否满足虚拟机vmi的资源要求，即

tagij＝(ppesj-vpesi)>0∧(pramj-vrami)>0

1.3给定主机pmj，定义该主机在t时刻的电源能耗表示为：

ej(t)＝cj+k*fj³(t)*uj(t)

其中cj为静态能耗标记，fj(t)为t时刻主机pmj的频率，uj(t)为t时刻主机pmj的功率(watt)，k为线性常量。

则在t时间内，主机pmj的能耗ej：

1.4判断所有虚拟机是否完成分配，若是则跳到1.6，否则跳到1.5。

1.5虚拟分层结构进行分配虚拟机操作(分配操作在下文2.2中会具体阐述)。跳转到1.4。

1.6结束算法，完成虚拟机初始化放置。

图2为虚拟分层结构图，图3为虚拟分层结构进行虚拟机分配步骤图。虚拟分层结构为进行虚拟机分配采用的结构模型。对于主机数量不同的情况，本发明采用不同的策略进行虚拟机的初始化，以提高数据中心资源利用率。具体分配步骤如下：

2.1由于构建和维护虚拟分层结构需要一定的系统开销，主机数量n小于4，即无法满足构建最小双层虚拟结构的数量2*2时，，则对于任意虚拟机vmi，定义其对应每个主机具有一个分配权重得分集合wi＝{wi1，wi2，…，wik}(其中k≥n)。定义wij为虚拟机vmi在主机pmj上的权重得分，wij＝h(vmi,pmj)。其中h()内包含约定的哈希函数，如hash32、hash64等。然后直接通过rendezvous哈希算法将虚拟机vmi分配给权重wij最大的主机pmj。如果主机pmk的性能是其他主机的h倍，则简单的表示pmkh次，例如pmk1和pmk2。显然，现在虚拟机分配到该主机上的概率是其他主机的2倍。此时，算法的运行时间为o(n)。

2.2针对主机数量n大于等于4，即满足构建最小双层虚拟结构的数量的情况，上述方法效果欠佳，需要建立虚拟分层结构(如图2所示)，改善算法运行时间。虚拟分层结构包含虚拟分层节点和真实主机节点簇两部分。虚拟分层节点之间以树的形式分布，其中，本发明将虚拟分层节点的所有叶子节点称为虚拟叶子节点扇区，虚拟分层节点构成的树的高度称为虚拟分层结构深度；真实主机节点簇是由多个真实主机构成的集合，与虚拟分层节点底部虚拟叶子节点相关联。

例如，实施例中，以主机数量n＝108为例。

构建的基本思想如下：

步骤2.2.1主机簇群划分。首先选择一个常数z，如虚拟分层架构图中所示，其中z为4，即每个簇中的主机数为4。将主机集合按照c＝ceiling(n/z)＝ceiling(108/4)＝27(其中ceiling函数表示将n除以z的值向上舍入为最接近的整数)c为27组织成簇。c0＝{cpm1，cpm2，…，cpmz}，c1＝{cpmz+1，cpmz+2，…，cpm2z}，…直至每个主机都归属于一个簇。每个簇为虚拟分层结构中的最底层节点。

步骤2.2.2虚拟叶子节点扇区以及虚拟分层结构深度确定。选择虚拟分层结构中每个子节点扇区的叶子数f，例如虚拟分层结构图中所示，每个子节点扇区的叶子数为3。叶子数即从根节点出发，每个节点有3个子虚拟节点。一般情况下f为一位整数，选择合适的f和z会使得到的算法效益和负载均衡度等和期望较相近。根据节点扇区的叶子数3以及主机簇个数4，可以得到虚拟分层结构的深度h：

f^h≥c

其中h是最小正整数，使得上述公式成立。因此，可以得到h＝3。

步骤2.2.3各虚拟叶子节点扇区编号。一般采用自然编号对每个扇区分别统一编号，例如从0，1，2，…，f-1。例子中为0，1，2，每一子节点都以0，1，2按序标号。

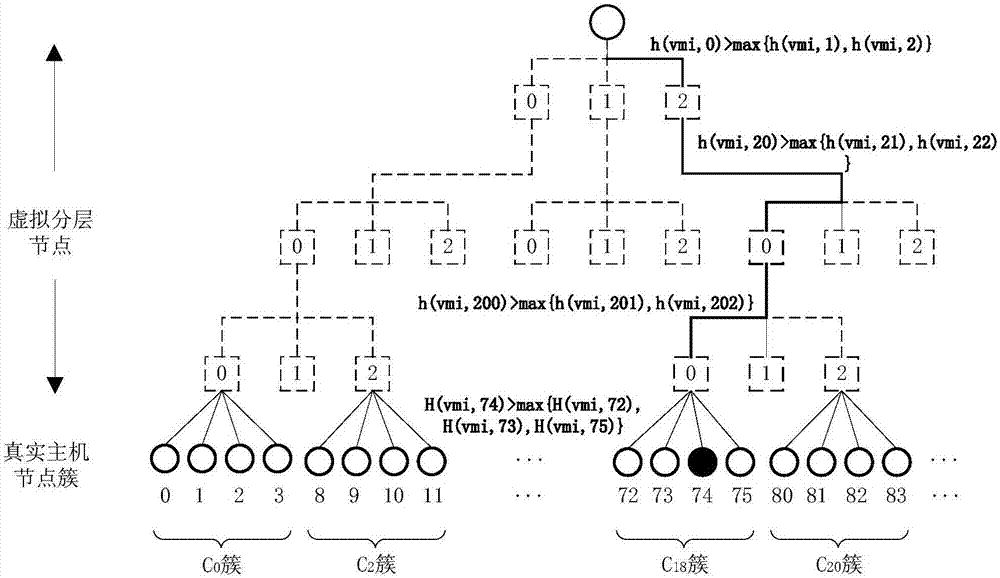
步骤2.2.4对于某一虚拟机vmi，对于任意一个虚拟节点s，都有一个对应的权重wis＝h(vmi,s)。在虚拟分层结构的每一层叶子扇区，都可通过rendezvous哈希算法计算各虚拟节点权重，选择得分最高的节点继续向下分层，直到选择至最底层的真实主机节点簇cl。如虚拟分层结构中，从根节点开始，因为h(vmi,2)>max{h(vmi,0),h(vmi,1)}，因此选择(2)3节点继续往下；在第二层三个子节点中，因为h(vmi,20)>max{h(vmi,21),h(vmi,22)}，因此选择(20)3节点继续往下；在第三层三个子节点中，因为h(vmi,200)>max{h(vmi,201),h(vmi,202)}，因此选择(200)3节点，即(200)3位置的真是节点簇，再进行下一步选择。

步骤2.2.5当虚拟机vmi选中真实主机节点簇cl后，在进行真实节点选择时，假设对于任意在真实节点簇cl中的主机节点cpmlz+j，都有一个对应的权重得分wi(lz+j)＝h(vmi,cpmlz+j)*tagi(lz+j)(若tag为false,则为0,若为true默认为1)。其中，将虚拟机vmi分配给主机cpmlz+j之后，h(vmi,cpmlz+j)为在相同t时间段内，eold与分配虚拟机vmi后的真实主机节点簇cl的总体能耗的比值，以及主机pmlz+j的资源利用率ulz+j与1的差方和对应权重常数的乘积的和：

其中ei+lz为t时间段内主机cpmlz+j的能耗，eold是指相同t时间段内，未分配新虚拟机时，真实主机节点簇cl的能耗。γ、δ是表示两者的权重。

步骤2.2.6因此，虚拟机vmi最终会选择使权重得分wi(lz+j)最高的主机节点完成分配，可以达到真实主机簇局部能耗最低的效果。图2中74节点为最终所选择的节点。

在虚拟分层结构中，虚拟节点的选择可以从任意层级进行，唯一的区别是产生的哈希次数有所差异，若从根节点开始选择，则直到选择到真实主机节点的过程中，一共需要的哈希值数量为count＝f*h次。其中f为每个子节点扇区的叶子数，h为虚拟分层结构的。

对于任何给定的虚拟机，通过rendezvous哈希算法以近乎相同的概率选择每个主机簇，并且rendezvous哈希算法复杂度为o(logn)，效率相对较高，且每一层虚拟节点的标识只是简单的数字基数前缀，可以轻松创建适当的经过排序的字符串表示。

在云环境中，经常会出现各种人为或自然原因导致物理主机宕机或删除、或者由于计算需求增大需要增加物理主机的情况。针对物理主机宕机或删除情况，本发明提出一种动态物理主机节点宕机或删除时的处理方案：

3.1对于给定虚拟机，若最终选择的真实主机节点资源不够分配导致不可用或已经宕机，可以选择权重值略高的同一簇中的真实主机节点完成分配。对虚拟分层结构中其他节点不产生影响。

3.2、对于给定虚拟机，若最终选择的真实主机节点资源不够分配导致不可用或已经宕机，且同簇下无法找到可用的真实主机节点进行分配，这种情况下，可以在虚拟分层结构中往上上升一个或多个层级，并从该层的同级虚拟节点中选择一个作为代替，再次将该层级降级到真实节点簇，寻找可用的真实主机节点。

针对物理主机增加情况，本发明提出一种物理主机节点的动态增加的处理方案：

3.3、当最后的主机簇还未满z时，可以直接将主机加入至该主机簇中。

3.4、当最后的主机簇的节点数为z时，且虚拟分层结构最底层未满时，可以增加一个主机簇。

3.5、当最后的主机簇的节点数为z时，且虚拟分层结构最底层也满时，可以将主机增加至第一个主机簇，这时，主机簇的常量z＝z+1。