基于马尔科夫链进化的汽车运行工况设计方法与流程

本发明涉及汽车运行工况设计方法，特别是一种基于马尔科夫链进化的汽车运行工况设计方法。

背景技术：

汽车的排放和能源消耗是汽车领域内备受关注的两个方面。而在寻找降低排放和提高燃油消耗使用率的新技术时，例如在考察某类车辆在某一地区排放水平或者能量消耗量时，确定当地的汽车运行工况，才能够提供可靠的检测依据；在设计开发新车型的动力系统时，汽车运行工况是重要的评价依据。汽车运行工况作为汽车正向开发过程中的一项核心技术，其中合理的设计方法是能够高效率得到代表性工况的关键。

在汽车运行工况设计方法中，基于马尔科夫链的设计方法已成为工况设计的主流方法。它依据工况是马尔科夫链的本质的特点，运用马尔科夫链随机模拟生成的工况序列。2001年，linjie在博士论文中提到汽车运行工况是一个随机过程，首次利用马尔科夫的方法设计工况。shishuming等人证明在小尺度范围内(如1s)，运行工况具有强马尔科夫性，即当前状态到下一时刻的状态存在确定的状态转移概率。研究学者又对工况的马尔科夫性进行了深入的拓展研究，yuebingjian等人通过试验数据验证了道路坡度具有马尔科夫性，设计了三参数的运行工况。马尔科夫链方法从符合工况动力学本质特征的客观事实出发，合理性强，富有科学依据。尽管马尔科夫模型在汽车运行工况中使用成熟，但是更多研究学者们关注的是马尔科夫链设计工况的应用以及拓展，并未注意到基于马尔科夫链设计汽车运行工况时，尤其设计多参数的高速工况时，存在设计效率极低的问题。因此，针对此问题提出本发明方法。

技术实现要素：

本发明的目的是提供一种基于马尔科夫链进化的汽车运行工况设计方法，以提高基于马尔科夫链方法设计多参数的高速工况的设计效率。

本发明基于马尔科夫链进化的汽车运行工况设计方法，包括以下五个阶段：

一、初始种群构建

通过汽车运行工况的马尔科夫链随机模拟生成多条满足一定长度的起止为怠速状态条件的工况状态序列，以此组成一个初始种群；具体步骤如下：

1)统计三参数(速度，加速度和坡度)工况原始数据库的状态转移矩阵：

首先，确定速度，加速度和坡度的划分步长以及范围，采用下式

st＝mt+(nt-1)×m+(pt-1)×m×h,t＝1,2,…

将三维空间状态mt,nt,pt转化为一维空间状态st，其中，mt为速度的状态，nt为加速度的状态，pt为坡度的状态，m为速度最大维数，h为加速度最大维数；

然后，采用最大似然估计方法，统计状态转移概率矩阵p，

其中，pij为一维空间状态si到一维空间状态sj的转移概率，nij为一维空间状态si到一维空间状态sj的转移频数，ni为一维空间状态si到一维空间的其他状态的转移频数之和，s为一维空间状态集合；

2)模拟马尔科夫链随机状态序列x＝(k0,k1,…,ki,…),i＝n，其中n为序列长度，

选取怠速状态作为马尔科夫链的初始状态x(1)＝k0，利用伪随机数原则，在0和1之间取随机数r1，选择满足

的状态k1作为马尔科夫链的下一状态x(2)＝k1，按照此模拟方法不断重复，生成长度为n的工况状态序列；选取终止状态仍为怠速状态的序列作为工况状态序列，依次生成多条起止为怠速状态的工况状态序列；

3)生成工况的初始种群

采用遗传算法中的整数编码方式，将马尔科夫链随机生成的状态编码为基因，将长度为n的工况状态序列编码为一条染色体，则多条染色体即多条工况状态序列组成一个初始种群；

二、目标函数设计

计算设计工况与参考数据库的所有指标的相对偏差，采用满意准则模型，将多目标转化为单目标的目标函数；具体步骤如下：

1)选取工况中常用的特征参数并设定允许偏差

选取汽车运行工况设计中常用的特征参数作为评价设计工况与原始数据库一致性的评价指标，允许偏差根据工程应用需求设定；

2)设计工况与原始数据库的指标函数一致性表达

x为生成的设计工况，io为原始数据库的特征参数，id为设计工况的特征参数，e为允许偏差，用公式(2)表达设计工况与原始数据库的一致性

|ioi-idi|≤ei,(i＝1,2,…,n),n＝11(2)

3)利用公式(3)满意准则模型的广义形式

将公式(2)转化为公式(4)

4)通过构造公式(5)辅助函数ti

把公式(4)多目标转化为公式(6)单目标函数f

三、交叉算子设计

利用汽车运行工况统计的状态转移矩阵，在任意两个个体序列中，判断与等长交叉段相关的四个基因转移概率是否非零，选择满足马尔科夫链状态转移关系的基因并进行等交叉段交叉，最终得到符合马尔科夫链的交叉个体；具体步骤如下：

下述中，x⁽¹⁾和x⁽²⁾为两条时间序列的个体，n为个体的长度，p为公式(1)计算得到的工况状态转移概率矩阵，

1)确定交叉位置

x⁽¹⁾的两个相邻基因和与x⁽²⁾的两个相邻基因和满足

时，i为x⁽¹⁾的交叉位置，j为x⁽²⁾的交叉位置，且i不一定等于j；为到的转移概率，为到的转移概率；

2)确定交叉段

为保证x⁽¹⁾和x⁽²⁾发生交叉后，生成的子代个体仍然满足长度为n，两个个体各自交叉位置之间的部分染色体长度必须相同；按照上述1)确定另一组交叉位置i′和j′，其满足

其中i′-i＝j′-j，为到的转移概率，为到的转移概率；

3)实施交叉，生成子代个体

确定交叉位置以及交叉段后，交换x⁽¹⁾中位置i到i′和x⁽²⁾中j到j′之间的部分染色体，最终生成两个子代染色体；

四、变异算子设计

应用汽车运行工况的马尔科夫链随机模拟，满足一定长度且起止为怠速状态条件下，生成任意一条工况状态序列作为子代序列个体；

变异算子采用上述阶段一2)中的马尔科夫链随机模拟方法进行设计，即满足一定长度且起止为怠速状态条件下，生成一定长度的工况状态序列，并对其整数编码，最后得到一条基因染色体作为变异个体；

五、代表性工况进化过程

设定迭代次数，进化初始种群至输出最佳目标函数值的工况状态序列；然后经过解码，生成三参数的时间序列，即代表性工况。

本发明设计方法，是通过马尔科夫链与遗传算法结合的思想，利用汽车运行工况的本质特征(马尔科夫链)去重新构建新的遗传算法，最后进化出代表性工况。该方法显著地提高了马尔科夫链方法设计多参数(速度、加速度和坡度)高速工况的效率。

在给定相同的三参数高速数据库下设计1800s长度的代表性工况，与基于传统马尔科夫链方法设计工况相比，平均用时减少了23.24小时，平均效率显著提高。在设计相同精度的代表性工况要求下，与基于传统马尔科夫链设计方法长时间仍未达精度要求相比，本发明方法得到更优的设计工况。该方法可以直接应用于处理马尔科夫链的实际问题中，改善马尔科夫链随机模拟的收敛慢的现象，具有更广泛的适用性。

附图说明

图1是本发明设计方法流程示意图；

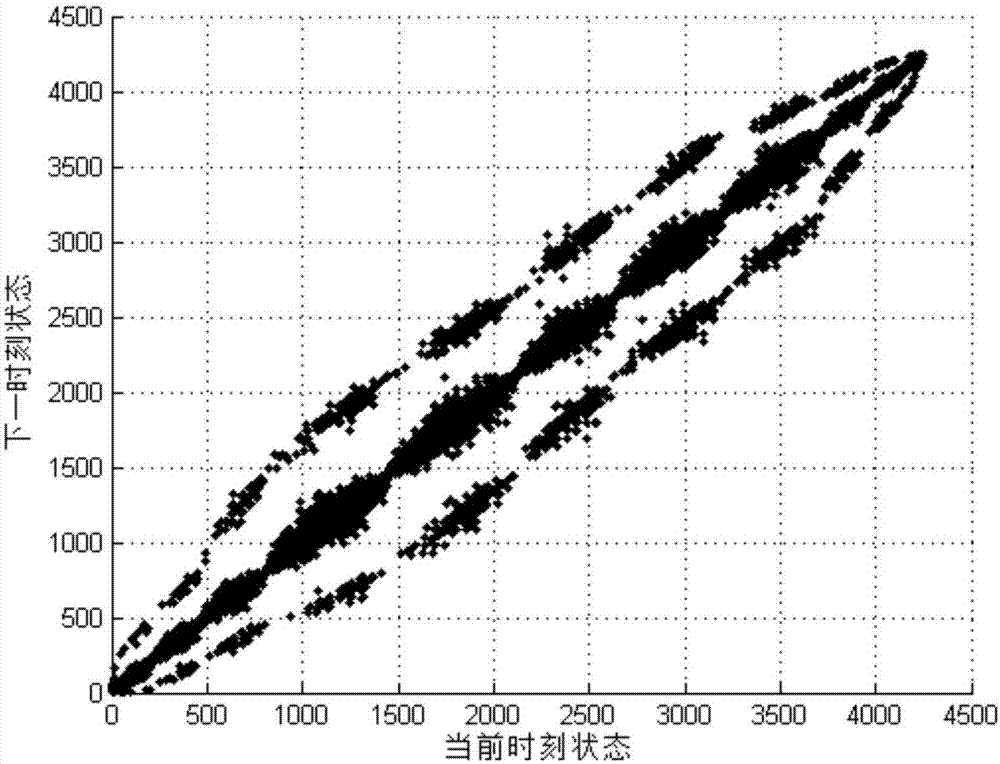
图2是本发明设计方法所述的状态转移概率矩阵二维投影图；

图3本发明设计方法所述的随机搜索交叉算法中循环次数k与发生交叉的概率的关系图；

图4本发明设计方法所述的随机搜索交叉算法中循环次数k与平均用时的关系图；

图5本发明设计方法所述的速度时间序列图；

图6本发明设计方法所述的加速度时间序列图；

图7本发明设计方法所述的坡度时间序列图。

具体实施方式

通过以下实施例及附图对本发明设计方法作进一步详细说明。

参照图1，本发明一种基于马尔科夫链进化的汽车运行工况设计方法，包括以下五个阶段，具体实施方式详述如下：

阶段一：初始种群构建

初始种群构建主要包括以下三个步骤：

1)统计三参数(速度，加速度和坡度)工况原始数据库的状态转移矩阵：

确定速度、加速度和坡度的划分步长以及范围。采用下式

st＝mt+(nt-1)×m+(pt-1)×m×h

将三维空间状态(mt,nt,pt)转化为一维空间状态st。其中，mt为速度的状态，nt为加速度的状态，pt为坡度的状态，m为速度最大维数，h为加速度最大维数。然后，采用最大似然估计方法，统计三参数工况的状态转移概率矩阵p，参见图2所示；

其中，pij为一维空间状态si到一维空间状态sj的转移概率，nij为一维空间状态si到一维空间状态sj的转移频数，ni为一维空间状态si到一维空间其他状态的转移频数之和，s为一维空间状态集合。

2)模拟马尔科夫链随机状态序列x＝(k0,k1,…,ki,…),i＝n，其中n＝1800

选取怠速状态作为马尔科夫链的初始状态x(1)＝k0，利用伪随机数原则，在0和1之间取随机数r1，选择满足

的状态k1作为马尔科夫链的下一状态x(2)＝k1，按照此模拟方法不断重复，生成长度为1800s的工况状态序列。选取终止状态为怠速状态的长度为1800s的序列作为工况状态序列；依次生成多条起止为怠速状态的工况状态序列。

3)生成工况的初始种群

采用遗传算法中的整数编码方式，将马尔科夫链随机生成的状态编码为基因。将长度为1800s的工况状态序列编码为一条染色体，则多条染色体即多条工况状态序列组成一个初始种群。初始种群大小设定为100。

阶段二：目标函数设计

目标函数设计主要包括以下4个步骤：

1)选取工况中常用的特征参数并设定允许偏差

选择和速度、加速度和坡度有关的11个特征参数，分别为怠速时间比例(％)、加速时间比例(％)、匀速行驶时间比例(％)、减速时间比例(％)、平均速度(km/h)、平均行驶速度(km/h)、行驶速度标准差(km/h)、pke(m/s³)、平均爬坡(％)、平均下坡(％)和va分布(velocityandaccelerationprobabilitydistribution)相关系数。允许偏差设定10％。

2)设计工况与原始数据库的指标函数一致性表达

x为生成的设计工况，io为原始数据库的特征参数，id为设计工况的特征参数，e为允许偏差。用公式(2)表达设计工况与原始数据库的一致性

|ioi-idi|≤ei,(i＝1,2,…,n),n＝11(2)

3)利用公式(3)满意准则模型的广义形式

将公式(2)转化为公式(4)

4)通过构造公式(5)辅助函数ti

把公式(4)多目标转化为公式(6)单目标函数f

阶段三：交叉算子设计

交叉算子设计主要包括以下三个步骤：

x⁽¹⁾和x⁽²⁾为两条时间序列的个体，n为个体的长度，p为由公式(7)计算得到的工况状态转移概率矩阵。

1)确定交叉位置

x⁽¹⁾的两个相邻基因和与x⁽²⁾的两个相邻基因和满足

时，i为x⁽¹⁾的交叉位置，j为x⁽²⁾的交叉位置，且i不一定等于j。为到的转移概率，为到的转移概率。

2)确定交叉段

为保证x⁽¹⁾和x⁽²⁾发生交叉后，生成的子代个体仍然满足长度为n。两个个体各自交叉位置之间的部分染色体长度必须相同。按照①确定另一组交叉位置i′和j′。其满足

其中i′-i＝j′-j，为到的转移概率，为到的转移概率。

3)实施交叉，生成子代个体

确定交叉位置以及交叉段后，交换x⁽¹⁾中位置i到i’和x⁽²⁾中j到j’之间的部分染色体，最终生成两个子代染色体。

每次执行随机搜索交叉算子，需要设定循环次数k以得到较高的发生交叉的概率。其中循环次数k与发生交叉的概率的关系见图3，循环次数k与平均用时的关系见图4，并设定k为200。

阶段四：变异算子设计

变异算子采用上述阶段一2)中马尔科夫链随机模拟生成起止为怠速的长度为1800的工况状态序列，并将其整数编码为一条基因染色体作为变异个体。

阶段五：代表性工况进化过程

设定迭代次数为100，进化初始种群至输出最佳目标函数值0.1的工况状态序列；然后经过解码，生成三参数的时间序列，即代表性工况，包括速度、加速度和坡度时间序列，分别见图5，图6和图7。