一种基于大间隔相对距离度量学习的行人重识别方法与流程

本发明涉及视频监控技术领域，具体涉及一种基于大间隔相对距离度量学习的行人重识别方法。

背景技术：

近年来，随着网络技术的发展以及社会安防需求的增长，智能视频监控的应用得到了大量的普及。由于视频监控能够以直观、准确、及时与丰富的图像展示当前状态或还原事发现场，成为了打击犯罪、公安刑侦、司法取证等工作的有效手段，也因此被广泛应用于各种场所。当前，在机关单位、小区、街道路口、车站、地铁等公共场合基本上建立起了比较完备的视频监控网络，它们所存储的视频为安全防范，实时监控跟踪以及事件分析提供了有效的数据保障。为了对比较大的范围进行有效的监控，当前的视频监控系统一般采用具有不重叠视域的摄像机对需要重点覆盖的区域进行监控。在一些基于视频监控系统的应用中，比如跨摄像机的行人跟踪与基于视频的行人检索中，常常需要根据特定的外观信息，对不同摄像机下的行人进行身份关联，即通过行人外观信息对不同摄像机捕获的行人画面进行匹配。这种对具有不重叠视域摄像机捕捉到的行人画面根据外观进行身份匹配的工作即为行人重识别。

但是由于不同摄像机的内部参数存在差异，行人在不同摄像机画面中受光照、摄像机视角与行人姿态等因素的影响，即使是同一行人在不同摄像机画面中的外观会存在巨大的差异，导致不同摄像机下根据行人外观进行身份匹配的重识别工作相当困难。

尽管行人重识别的方法各有不同，但总体上大致都可以分为两个阶段。第一阶段是特征表达的提取，即从行人画面(已从摄像机监控视频中裁切出)中计算一些具有判别性的特征表达，获得关于行人外观的数字化表达。第二阶段是采用一些距离/相似度计算方法计算不同摄像机下的两张行人画面间的距离/相似度，并确定两张图像中的行人是否为同一人；针对第二阶段的距离度量研究中，传统方法一般采用标准的距离函数度量行人间的相似性，如欧式距离、巴氏距离等，但是，其存在距离度量的鲁棒性差的问题，导致行人重识别的准确率低。

技术实现要素：

本申请提供一种基于大间隔相对距离度量学习的行人重识别方法，包括步骤：

在训练数据集中，对不同摄像机下的行人图像的特征表达向量进行降维处理，并将降维处理后的特征表达向量投影到类内子空间；

根据投影后的各特征表达向量及其对应的标签信息通过优化损失函数学习马氏距离度量矩阵；

在测试数据集中，利用从训练集中学习获得的马氏距离度量矩阵对不同摄像机下的行人图像进行行人重识别。

一种实施例中，对不同摄像机下的训练数据集的行人图像的特征表达向量进行降维处理，具体为：

将训练数据集中摄像机a下行人图像的特征表达向量拼成矩阵将训练数据集中摄像机b下行人图像的特征表达向量拼成矩阵其中d为特征向量的维度，n和m为特征表达向量的个数；

首先将x与z拼接为矩阵并计算其中所有样本的均值向量其中yi指代矩阵y的第i列；

对摄像机a和摄像机b下的行人图像的特征表达向量分别作去均值处理，即对矩阵y执行运算其中1n+m为n+m维元素全为1的列向量；

计算中所有去均值后样本的协方差矩阵；

对所述协方差矩阵进行特征值分解运算，并获取前d′个最大特征值所对应的特征向量；

将所述前d′个最大特征值所对应的特征向量拼成pca投影矩阵：

分别将摄像机a和摄像机b下的特征表达矩阵x与z使用所述pca投影矩阵wpca向低维空间作投影运算，获得降维后的矩阵：和其中1n与1m为n维与m维元素全为1的列向量。

一种实施例中，将降维处理后的行人图像的特征表达向量投影到类内子空间，具体为：

计算降维后的所有特征表达向量的类内协方差矩阵：其中，为所有具有相同身份标签的跨摄像机行人图像对所组成的集合，x′i与z′j分别为x′与z′的第i、j列，指代x所属摄像机下的第i张图片与z所属摄像机下的第j张图片，x′i与z′j为同一行人在不同摄像机下的特征表达向量；

对所述类内协方差矩阵进行特征值分解运算，获取按降序排列的各特征值所对应的特征向量，并拼成类内子空间投影矩阵：

分别将降维处理后的行人图像的特征表达向量使用所述类内子空间投影矩阵wintra投影到类内子空间,采用矩阵运算为：其中，为一个对角矩阵，主对角线上的元素为按降序排列的各特征值的平方根倒数。

一种实施例中，根据向类内子空间投影后的特征表达向量及其对应的标签信息通过优化损失函数学习马氏距离度量矩阵，具体为：

目标函数为：其中，为在摄像机b下的正确匹配图像特征表达向量集合，而则为在摄像机b下的错误匹配图像特征表达向量集合，为关于三元组的函数，用于约束与错误匹配图像中最的小距离比正确匹配距离高于一个常数阈值δ，为马氏距离函数，其由一个半正定矩阵m所参数化；

采用加速邻近端梯度优化方法对所述目标函数求解，获取最优马氏距离度量矩阵。

一种实施例中，利用所述在训练集上学习获得的马氏距离度量矩阵对测试数据集中不同摄像机下的行人图像进行行人重识别，具体为：将测试数据集中摄像机a下每一张图片的特征表达向量与摄像机b下所有图像提取的特征表达向量两两计算马氏距离，并按马氏距离由小到大排序，将马氏距离最小的图像作为正确匹配的图片对。

一种实施例中，还包括获取数据集中所有图像的特征表达向量的步骤：

对行人图像大小进行归一化处理；

对归一化处理后的行人图像进行特征表达向量提取；

将所有行人图像的特征表达向量与其所对应的标签划分为训练数据集和测

试数据集。

依据上述实施例的行人重识别方法，由于先对训练数据集中的特征表达向量进行降维，再将降维后的特征表达向量投影到类内子空间，进而在类内子空间通过相对距离比较学习马氏距离度量矩阵，最后，在测试集上使用学习到的马氏距离度量矩阵进行行人重识别，该方法能够有效避免训练数据集中正、负样本不平衡所带来的影响，能够学习到鲁棒性强的马氏距离度量矩阵，提升行人重识别的准确率。

附图说明

图1为行人重识别方法流程图；

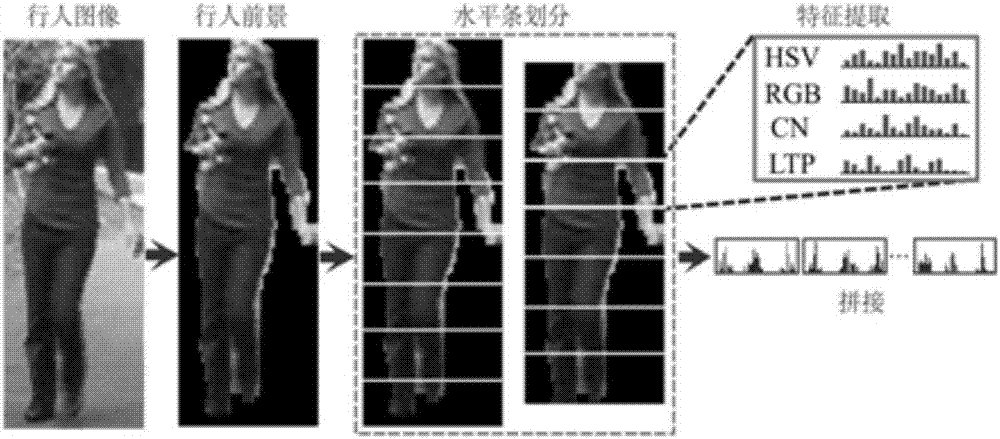
图2为特征表达向量提取过程示意图；

图3为一公开数据集中的不同摄像机下部分行人图片示意图；

图4为行人重识别方法仿真结果比较图。

具体实施方式

下面通过具体实施方式结合附图对本发明作进一步详细说明。

为了避免在度量学习中正确匹配行人图片对的数量远低于不同行人图片对所带来的样本不平衡问题，本例提供一种基于大间隔相对距离度量学习的行人重识别方法，通过将样本投影到类内子空间，采用新设计的具有更强约束的损失函数，使本例提出的行人重识别方法能够获得更优的距离度量矩阵，从而大大提高行人重识别的准确率。

本例以从监控视频画面中裁剪出的仅包含行人的矩形画面作为行人图像，提取这些行人图像的特征表达向量，并将这些特征表达向量及对应的身份标签所组成的数据划分为训练数据集和测试数据集，在训练数据集上，按大间隔相对距离度量学习算法学习得到马氏距离度量矩阵，在测试数据集上利用学习到的距离度量矩阵计算不同摄像机下行人画面的距离，实现行人身份验证(即完成行人重识别工作)，具体包括如下步骤，其流程图如图1所示。

s1：获取行人图像的特征表达向量，并划分为训练数据集与测试数据集。

具体的，对行人图像大小作归一化处理，即将所有行人图像统一到相同的大小；利用现有的特征表达向量提取算法计算归一化处理后的行人图像的特征表达向量，将所有行人图像的特征表达向量与其所对应的标签(如，行人身份验证标签)组成数据集，再将数据集划分为训练数据集和测试数据集。

其中，对行人图像大小归一化处理的具体过程是：如图2所示，给定一张行人图像，首先将该行人图像调整为128像素×64像素，然后采用前景分割算法获得图像中的行人。再对前景行人图像划分为8个等高度的水平条，对于最顶端与最底端分别去除1/2水平条高度后，将获得的裁剪后的图像再划分为7个等高水平条，这样的划分可以获得具有覆盖的15个水平条；从每个水平条中分别提取hsv联合直方图、rgb联合直方图、尺度不变局部三元模式(localternarypattern,ltp)纹理特征与显著颜色名称(salientcolornames,scn)直方图。其中，hsv与rgb联合直方图每个颜色通道作8位量化，因此，获得的hsv/rgb联合直方图均为512维，ltp直方图为182维，scn直方图为16维；将各个水平条上提取的特征向量按顺序逐一拼接起来，得到整幅图像完整的特征表达向量，最终的维度为18030。

s2：在训练数据集中，对不同摄像机下行人图像的特征表达向量进行降维处理并将降维处理后的特征表达向量投影到类内子空间。

为了提高运算速度，对不同摄像机下的行人图像的特征向量首先进行无监督的pca降维处理，且，降维时采用保留所有能量的方案，降维处理的具体过程如下。

将训练数据集中摄像机a下行人图像的特征表达向量拼成矩阵将训练数据集中摄像机b下行人图像的特征表达向量拼成矩阵其中d为特征向量的维度，n和m为特征表达向量的个数；

首先将x与z拼接为矩阵并计算其中所有样本的均值向量其中yi指代矩阵y的第i列；

对摄像机a和摄像机b下的行人图像的特征表达向量分别作去均值处理，即对矩阵y执行运算其中1n+m为n+m维元素全为1的列向量；

计算中所有去均值后样本的协方差矩阵；

对所述协方差矩阵进行特征值分解运算，并获取前d′个最大特征值所对应的特征向量；

将所述前d′个最大特征值所对应的特征向量拼成pca投影矩阵：

分别将摄像机a和摄像机b下的特征表达矩阵x与z使用所述pca投影矩阵wpca向低维空间作投影运算，获得降维后的矩阵：和其中1n与1m为n维与m维元素全为1的列向量。

另外，将降维处理后的行人图像的特征表达向量投影到类内子空间的过程如下。

计算降维后的特征矩阵的类内协方差，获取类内协方差矩阵：

其中，为所有具有相同身份标签的跨摄像机行人图像对所组成的集合，x′i与z′j分别为x′与z′的第i、j列，指代x所属摄像机下的第i张图片与z所属摄像机下的第j张图片，x′i与z′j为同一行人在不同摄像机下的特征表达向量；

对类内协方差矩阵进行特征值分解运算，获取按降序排列的各特征值所对应的特征向量，并拼成类内子空间投影矩阵：

分别将降维处理后的行人图像的特征表达向量使用所述类内子空间投影矩阵wintra投影到类内子空间：

其中，中为一个对角矩阵，主对角线上的元素为按降序排列的各特征值的平方根倒数。

通过公式(2)向类内子空间投影操作能够有效地抑制具有较大方差的特征向量的维度，从而使得具有相同标签的跨摄像机特征向量间的距离得到降低。

s3：根据投影后的特征表达向量及其对应的标签信息通过优化损失函数学习马氏距离度量矩阵。

本例中，从跨摄像机的行人图像特征表达向量及对应的标签中学习马氏距离度量矩阵的目标函数的表达式如下：

其中，为在摄像机b下的正确匹配图像集合，而则为在摄像机b下的错误匹配图像集合，为关于三元组的函数，用于约束与错误匹配图像中最的小距离比正确匹配距离高于一个常数阈值δ，为马氏距离函数，其由一个半正定矩阵m所参数化；并将作为约束函数。

公式(3)中采用了log-logistic损失函数，能够为正确匹配样本对与错误匹配样本对提供一个柔性区分间隔，此外该函数为一凸函数，保证了公式(3)为凸优化问题其最优解唯一，该函数的光滑可微性也为公式(3)的优化求解带来了方便。此外，采用了三元组来比较的正确匹配图像对与所有错误匹配图像对间的相对距离，避免了从不平衡数据中学习到的度量矩阵不够鲁棒的缺点；而约束了即使的错误匹配图像中即使最小的距离也要比正确匹配距离高出δ，这是一个非常严格的约束条件，保证了正确匹配图像在最终按距离排序时，其位置能够有效地被向前推(toppush)。

另外，本例采用了高效的加速邻近端梯度(acceleratedproximalgradient,apg)优化方法对公式(3)进行求解，获取最优马氏距离度量矩阵。具体的，为了更高效方便地求解公式(3)，首先对公式(3)进行恒等变换，将约束条件采用示性函数整合到目标函数中：

式中为关于矩阵m是否属于d′×d′大小半正矩阵集合的示性函数，其中，

进一步，将公式(4)拆分为如下两部分：

采用apg的迭代优化策略，首先对f(m)执行梯度下降，再优化h(m)，如此迭代直到达到收敛条件阈值。令vt(t≥1)为已搜索到的最优点，在此点处对f(m)线性化，创建邻近点算子(proximaloperator)如下：

其中，||·||f为frobenius范数，<·>为矩阵内积运算，ηt为步长值。式中为函数f(m)在vt点的梯度；

进一步，

其中，

为了加快对(9)的运算速度，避免公式(12)中的外积运算所带来的巨大运算量，实际数值运算采用了矩阵化运算，

式中n+为对每个a摄像机下每个在摄像机b下作添补后的正确匹配图片数，这样使得对于所有在摄像机b下都具有相同的正确匹配图片数，从而可以进行矩阵化运算。g^(t)为一个3维矩阵，其中的元素为为g^(t)中第2个维度上的第l个2维矩阵，与是两上对角矩阵，它们主对角线上的元素的和分别为的行和与列和。采用式(13)的计算效率远高于式(9)，特别是在n+＝1的情况下，即对每个摄像机a下的行人图片，在摄像机b下仅有1张正确匹配图片。

对式(8)丢弃与m无关项f(vt)，并添加可获得其等价形式：

从而获得解

接下来根据apg优化h(m)，即将向半正定锥投影。首先对作特征值分解，取后获得

接下来，根据获得的mt与前一步获得的mt-1作外插值获得vt+1，即其中

重复上述步骤直到即算法收敛(∈为指定的收敛阈值)，此时获得的mt即为所求最优马氏距离度量矩阵m(亦即式(3)的解)。

以viper数据集为例，如图3所示展示了从该数据集中随机选取的部分行人图像示例。将数据集随机划分为不相交的两部分，其中一部分作为训练数据集，另一部分作为测试数据集，如在viper上，将其中包含的632个行人(每个行人在两个摄像机下各一张图片)随机划分为2个各含316个行人子集，前316人图片的向类内子空间投影后的特征表达向量用于训练，后316人投影后的特征表达向量用作为测试集。

以举例说明学习获得马氏距离度量矩阵的具体过程如下：

步骤1：初始化m0与v1均为d′×d′大小的单位阵，θ0＝1，收敛阈值∈＝10^-5；

步骤2：更新θt+1：

步骤3：对每个摄像机a下的行人图片，使用当前迭代中获得的mt按计算其与所有摄像机b下的行人图片间距离，并根据式(15)获得与其距离最小的错误匹配图片序号；

步骤4：按公式(10)与(13)计算梯度

步骤5：采用线搜索方法估计式(8)中的步长ηt；

步骤6：按式(14)计算f(m)在vt点处的最优解在

步骤7：将向半正定锥投影获得第t步迭代中式(3)的最优解mt；

步骤8：更新vt+1：

步骤9：根据式(4)计算损失函数，如果当前损失函数与上次损失函数差值大于收敛阈值∈，则转到步骤2，否则认为算法收敛，输出最优解mt。

s4：在测试数据集中，利用马氏距离度量矩阵对摄像机a和摄像机b下的行人图像进行行人重识别。

具体为：将测试数据集中摄像机a下每一张图片的特征表达向量与摄像机b下所有图像提取的特征表达向量两两计算马氏距离，并按马氏距离由小到大排序，将马氏距离最小的图像作为正确匹配的图片对；即，对所有测试数据集中的特征表达向量使用wpca与均值特征向量作pca投影到d′维度，再使用wintra向类内子空间投影，对测试数据集中摄像机a下一个行人图像的向类内子空间投影后的特征表达向量，与摄像机b下的所有行人图像的类内子空间投影后特征表达向量根据计算马氏距离，对获得的距离按距离由小到大升序排列，排在靠前位置的被认为与摄像机a下行人图像最为匹配的摄像机b下行人图像，重复计算马氏距离及排序操作，直到摄像机a下所有行人图像都有摄像机b下所有行人图像完成距离计算与排序操作。

如图4所示，为本例与其它公开方法在viper数据集上的重识别累积匹配准确率(cumulativematchingcharacteristic,cmc)曲线，其中sssvm为每个行人训练一个svm分类器，并采用最小二乘半耦合词典创建特征空间与分类器空间之间的对应关系；nfst将行人图片的特征表达向量投影到类内散布矩阵的零空间再进行匹配，该方法能够有效地解决小样本问题且具有闭合形式的解；mlapg方法在求解度量矩阵时对正、负样本对采用了不对称加权的策略来解决样本不平衡导致的度量矩阵不够鲁棒的缺点；xqda方法在求解距离度量矩阵的同时还求解一个低维投影矩阵，从而无需先对特征向量降维再学习度量矩阵；polymap方法对跨摄像机的行人图片特征向量首先采用二次多项式核函数进行映射，再学习相似度函数计算不同摄像机下图片之间的相似度；mlf方法通过学习中层滤波器特征，利用ranksvm算法来计算行人图片间的相似度，但运算耗时较长；salmatch方法采用了对行人图片首先计算其显著性图，再使用该显著性图对ranksvm计算的相似度进行加权；kissme为从统计推理角度出发提出的一种快速度量学习方法，该算法简单高效，具有闭合形式的解，但是对pca维度相当敏感；pcca方法从训练样本中学习到一个低维投影矩阵，因此可以直接处理高维样本，并在降维后的子空间中实现行人图片的匹配；prdc方法从概率角度出发，旨在学习一个投影子空间使得错误匹配图像间距离高于正确匹配图像间距离的概率最大化。lmrdl为本发明实施例的准确率结果。可以看出本实施例在识别准确率明显优于其他方法。此外，由于采用了高效的apg优化方法，本发明方法求解速度也很快。

与现有技术相比，本发明具有以下的有益效果：

传统的度量学习往往直接不同摄像机下的行人图像对施加硬约束，即匹配图像对的距离应小于某一阈值，而不匹配图像应大于此阈值。但这种约束过于僵硬，因为无法保证不同行人的两张图像均满足固定的阈值条件，另外受到不平衡数据的影响较重。以往的基于三元组的度量学习方法或者不处理类内图像对，或者在目标函数中同时约束类内距离与类间距离，但需要对两者进行平衡。而本发明所提出的度量学习方法是在将样本投影到内类子空间后再学习相对距离度量，该方法不仅能够有效地避免不平衡样本所带来的度量矩阵不够鲁棒的缺点，还能够降低不同摄像机下类内行人图像的距离，不必对类内距离与类间距离进行平衡。在行人重识别任务上的实验结果证实了本发明提出的方法的有效性。

以上应用了具体个例对本发明进行阐述，只是用于帮助理解本发明，并不用以限制本发明。对于本发明所属技术领域的技术人员，依据本发明的思想，还可以做出若干简单推演、变形或替换。