一种基于卷积受限玻尔兹曼机的形状建模方法及相关装置与流程

本发明涉及图像处理领域，具体涉及到采用卷积受限玻尔兹曼机对同类但具有差异的目标形状建模。

背景技术：

对图像中的目标形状建模，得到的形状能够完整地表达目标的轮廓，为后续的图像分割、分类、目标检测等任务打下基础。如当把形状应用到图像分割领域时，由于形状能表达出目标的轮廓，所以把形状与目标对准之后，能够很好的把目标从背景中割离出来，达到理想的分割结果。

受限玻尔兹曼机(rbm)是由smolensky提出的，是一个生成模型，该模型包含两层结构，即可视层和隐层，这两层之间节点是全连接的，同层的各节点之间是无连接的。由于该模型把输入图像拉成一维的向量作为输入，忽略了图像之间的二维结构信息，所以当用该模型来采样生成形状时，很容易忽略细节，使采样出的形状比较模糊。

技术实现要素：

有鉴于此，本发明实施例提供了一种基于卷积受限玻尔兹曼机的形状建模方法、装置及电子装置，至少部分的解决现有技术中存在的问题。

第一方面，本发明实施例提供了一种基于卷积受限玻尔兹曼机的形状建模方法，包括如下步骤：

在受限玻尔兹曼机的基础上增加卷积属性，得到卷积受限玻尔兹曼机的模型结构；

基于所述卷积受限玻尔兹曼机模型，得到所述卷积受限玻尔兹曼机模型的数学表达以及模型的训练方式；

确定实验所用模型的结构，用训练集训练模型，用该模型进行建模形状的实验。

根据本发明实施例的一种具体实现方式，所述方法还包括：

在用模型进行建模形状之前，先确定模型的网络结构，之后再训练及测试网络，其中，模型结构的确定，包括确定网络的层数、卷积核的个数、每一层特征图的个数。

根据本发明实施例的一种具体实现方式，所述方法还包括：

在模型结构确定后，选定训练集来确定模型中参数的值，其中，训练集和测试集从weizmannhorse数据集中选择，该数据集中共有328幅图像，将其中的200幅图像用于训练网络，其余的128幅图像用于测试。

根据本发明实施例的一种具体实现方式，所述方法还包括：

在模型训练好后，用训练集和测试集图像分别来测试模型。

根据本发明实施例的一种具体实现方式，所述用训练集和测试集图像分别来测试模型，包括：

用训练集和测试集中完整的图像作为模型的输入，来测试模型的表达能力和生成形状的能力；

对训练集和测试集中的图像添加均匀噪声和高斯噪声干扰，以添加了噪声的图像作为模型输入，以此来测试模型的抗噪能力。

第二方面，本发明实施例提供了一种基于卷积受限玻尔兹曼机的形状建模装置，包括：

增加模块，用于在受限玻尔兹曼机的基础上增加卷积属性，得到卷积受限玻尔兹曼机的模型结构；

获得模块，用于基于所述卷积受限玻尔兹曼机的模型，得到所述卷积受限玻尔兹曼机的模型的数学表达以及模型的训练方式；

确定模块，用于确定实验所用模型的结构，用训练集训练模型，用该模型进行建模形状的实验。

第三方面，本发明实施例提供了一种电子装置，所述电子装置包括：

至少一个处理器；以及，

与所述至少一个处理器通信连接的存储器；其中，

所述存储器存储有可被所述至少一个处理器执行的指令，所述指令被所述至少一个处理器执行，以使所述至少一个处理器能够执行第一方面及其任一实现方式中所述的方法。

本发明的目的在于提出对图像中的目标建立形状模型的方法，并提出了通过深度学习方法建立形状模型，用同类但姿态各异的目标训练模型，通过该模型表达该类目标的概率分布，从而实现目标的多种形态表达，并可通过采样生成形状。

附图说明

为了更清楚地说明本发明实施例的技术方案，下面将对实施例中所需要使用的附图作简单的介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其它的附图；

图1是rbm模型的网络结构；

图2是crbm模型的网络结构；

图3是crbm的具体构造过程；

图4是rbm模型的采样过程；

图5是crbm模型的采样过程；

图6是仿真实验的训练样本；

图7是训练集和测试集图像作为输入采样得到的结果；

图8是训练集和测试集添加均匀噪声图像作为输入采样得到的结果；

图9是训练集和测试集添加高斯噪声图像作为输入采样得到的结果。

具体实施方式

下面结合附图对本发明实施例进行详细描述。

应当明确，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其它实施例，都属于本发明保护的范围。

本发明的目的在于提出对图像中的目标建立形状模型的方法，并提出了通过深度学习方法建立形状模型，用同类但姿态各异的目标训练模型，通过该模型表达该类目标的概率分布，从而实现目标的多种形态表达和生成。

本发明提出的建模方法是一种基于卷积受限玻尔兹曼机的形状建模方法，并与受限玻尔兹曼机建模形状的方法进行对比。具体步骤为：首先，在受限玻尔兹曼机的基础上，引入“卷积”的概念，给出卷积受限玻尔兹曼机的模型结构，同时还给出模型的特点；接着，给出该模型的数学表达以及模型的训练方式、采样方法；最后，确定实验所用模型的结构，用训练集训练模型，用该模型进行建模形状的实验。

下面对各步骤做进一步的具体描述。

受限玻尔兹曼机rbm是一个两层的无向图模型，即具有一个可视层v和一个隐层h，层内无连接，两层之间是全连接的，rbm是一个生成模型，其网络结构如附图1所示。

假设附图1的rbm网络结构有n个可视节点和m个隐节点，其中每个可视节点只和m个隐节点相关，和其他可视节点是独立的，即可视节点的状态只受m个隐节点的影响，反之隐节点也是，只受n个可视节点的影响。无论是可视节点还是隐节点，每个节点的值代表了该节点当前的状态。

对rbm来说，当图像维度比较高或者图像比较大时，模型的规模变的很大，训练参数增多。而cnn的网络机制让这个模型很适合处理自然图像，对输入图像的大小没有要求，不论图像大小，不会增加模型的规模，并且还提供了图像的空间结构信息，更重要的是减少了要训练的参数个数。为了解决rbm在图像应用中存在的问题，把cnn引入rbm，提出卷积受限玻尔兹曼机crbm。

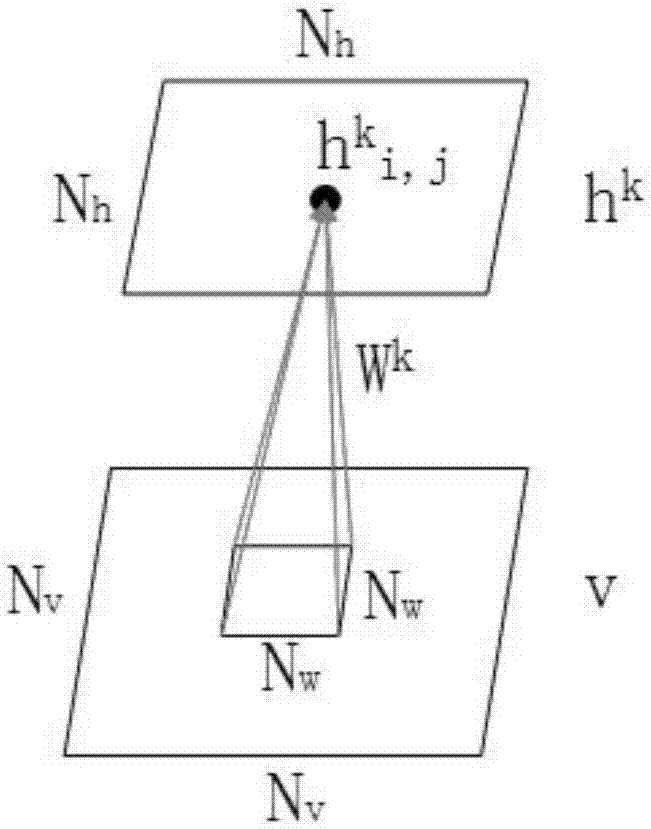
卷积受限玻尔兹曼机crbm在结构上与rbm相似，只有两层结构，即输入层v和隐层h，同时该模型仍然是生成模型。与rbm不同的是，crbm的输入层是一幅图像，模型的特点是局部感受野和权值共享，即隐层和输入层是局部连接，权重在图像的任何位置是共享的。模型结构如附图2所示，为了方便，这里只是展示了隐层的一组。

在该模型中，假设输入图像大小为nv×nv，那么模型的输入层由nv×nv大小的二维矩阵组成，隐层有k组，每组代表隐层的一个特征图，是大小为nh×nh的二维矩阵，共有k×nh×nh个隐层单元。每一个组都与一个大小为nw×nw的卷积核相连(nw＝nv-nh+1)。另外，所有的输入层单元共享同一个偏置c，隐层的每一个组内的所有单元共享同一个偏置bk，即隐层有k组，那么就对应有k个偏置。

附图3表示了crbm模型的构造过程，即由v获得h的过程。在该图中，输入是一个6×6大小的二维图像，卷积核的大小是3×3，隐层有k个特征图，不同颜色的线代表不同的卷积核，同种颜色的线代表的是同一个卷积核。以图中蓝色的线为例，蓝色的线代表的是第k个卷积核，该卷积核从输入图像的左上角开始，与输入图像3×3大小的区域做卷积运算，得到第k个特征图hk左上角第一个位置的值，然后该卷积核依次水平、竖直方向移动，与输入图像做卷积运算，不断得到hk各个单元的值，直到输入图像的最后一个位置，如附图3中右下角通过蓝色线连接的hk的最后一个单元与输入图像最后一块3×3大小的区域。通过这一过程可以得到隐层的一个组，从而构建出隐层h。

用向量v和h分别表示可视层单元和隐层单元的状态向量，即v＝(v1，v2，…，vn)，h＝(h1，h2，…，hm)，其中vi表示第i个可视单元的状态，hj表示第j个隐单元的状态。在这里，假设所有的可视单元和隐单元均为二值变量，即i，j，vi∈{0，1}，hj∈{0，1}，那么对于一组给定的状态(v，h)，该模型的能量定义为：

其中θ＝{wij，ai，bj}，i＝1，2，...，n；j＝1，2，...，m

参数说明：v——司视层单元的状态向量；

h——隐层单元的状态向量；

vi——可视层第i个单元的值；

ai——可视层第i个单元的偏置；

n——可视层单元的个数；

hj——隐层第j个单元的值；

bj——隐层第j个单元的偏置；

m——隐层单元的个数；

wij——可视层第i个单元与隐层第j个单元的连接权重。

根据能量函数，可以得到(v，h)的联合概率分布：

其中，z(θ)是归一化常量。

由联合概率分布可以得到边缘概率分布：

由于rbm特殊的结构，即层内无连接，层间全连接，隐单元的状态之间是相互独立的，其状态只与可视层单元的状态有关；相反的，可视层单元的状态也是相互独立的，只与隐层单元的状态有关，所以可得边缘概率分布为：

隐单元和可视单元的激活概率为：

其中为sigmoid函数。

训练rbm模型，就是要在给定输入的情况下，确定该模型中的参数θ，从而拟合给定的训练数据，所用的算法是由hinton提出的cd算法，目前该算法已成为训练rbm的标准算法。

在rbm中，可视单元数一般等于训练数据的特征维数，而隐单元数需要事先给定。

在定义模型的能量函数前，为了之后的叙述方便，在这里做一些假设以及符号说明。首先假设输入的是二值的图像，1代表目标，0代表背景。其次，*表示卷积，·表示两个矩阵的的乘积，表示对矩阵a进行180度旋转。

定义模型的能量函数：

其中k＝1，2，…，k；r＝1，2，…，nw，s＝1，2，…，nw

参数说明：k——有k个卷积核，也就是隐层h有k个特征图；

nh——隐层h的每个特征图的大小；

nw——每个卷积核的大小；

nv——输入层v的大小；

——隐层h第k个特征图的节点(i，j)的值；

——与隐层相连的第k个卷积核的节点(r，s)的值；

vi+r-1，j+s-1——输入层v的节点(i+r-1，j+s-1)的值；

bk——隐层h的第k个特征图的偏置；

c——输入层v的偏置。

用之前定义的符号表示能量函数为：

得到模型的联合概率分布：

由联合概率分布可以得到条件概率分布：

其中为sigmoid函数。

训练crbm模型，采用的是和rbm同样的训练算法——对比散度(cd)算法。训练开始之前，要确定模型的结构、学习率等参数。

rbm模型训练好后，也就是模型的参数确定了，就可以用来生成形状。采用的方法是多步gibbs采样，采样的过程如附图4所示。给定一个输入图像，即确定了模型可视层单元节点的状态，根据p(h|v)确定隐单元节点的状态，也就是附图4中的“1”；当隐单元状态确定后，根据p(v|h)确定可视层单元新的状态，也就是附图4中的“2”；如此重复，不断的进行步骤“1”和“2”，也就是附图4中的“3”、“4”……“n”，直到收敛，然后由第n步就可以得到由rbm生成的形状。

模型训练好后，可用该模型生成形状，采用的方法和rbm一样，都是多步的gibbs采样，过程如附图5所示，图中由第n步采样得到的v就是由crbm生成的形状。

实验数据为weizimannhorse数据集，该数据集包括三种类型的图像：彩色图、灰度图、二值图，在该实验中用的是该数据集中的二值图，选择200幅图像作为训练集，128幅作为测试集，并且把所有图像都归一化到32*32大小，训练集中的图像如附图6所示。由附图6可以看出，训练集中的马形态各异，马的头都是朝向一个方向。

下面结合附图表和实施例对本发明进一步说明。

实验环境为win10系统下安装的matlabr2014a，电脑配置为intel(r)xeon(r)cpuf5-2690，2.66hz，2566bram。在该实验中，crbm的参数设置如下：卷积核的大小nw为3，个数k为20，学习率为0.05，迭代次数为1000。rbm的参数设置为：可视层和隐层的单元个数分别为1024和500，学习率为0.05，迭代次数为1000。

本发明提出的模型crbm与rbm在同一个数据集上训练，crbm的训练时间是503.54s，rbm的训练时间是245.54s。

训练集和测试集完整的图像作为输入。从两个模型中采样得的结果如附图7所示。

附图7分别展示了训练集和测试集中的五幅图像。附图7的(a)和(b)分别是训练集图像和测试集图像作为输入，从rbm和crbm中采样得到形状，其中(a)列是输入图像，(b)列是rbm的采样生成形状的结果，(c)列是crbm生成形状的结果。从附图7的结果图中可以直观地看到，crbm的形状生成效果比rbm的要真实，更符合实际，rbm模型生成的形状比较模糊，很容易缺失细节，如马腿，而crbm则很好地保留了马的细节信息，重构出来的马与输入比较相近。为了定量表达二者的差异，采用欧氏距离这一指标来衡量生成形状与原始图像的差异，对于训练集来说，rbm采样生成的形状的平均欧氏距离是7.6826，crbm模型生成形状的平均欧氏距离是3.8946；对于测试集来说，rbm采样生成的形状的平均欧氏距离是8.3314，crbm模型生成形状的平均欧氏距离是4.5842。

训练集和测试集图像添加10％的服从(0，1)分布的均匀噪声作为输入。得到的结果如附图8所示。

附图8展示的只是训练集和测试集中的五幅图像。附图8中(a)和(b)分别表示训练集和测试集中的图像添加噪声之后的采样生成形状的结果，其中(a)列表示的是原始的未添加噪声的图像，(b)列表示的是对(a)列中的图像添加噪声，(c)列和(d)列分别表示的是rbm和crbm采样生成形状的结果图。从附图8中可以直观的看出，无论是训练集还是测试集中的图像，这两个模型都能有效的去除噪声的影响，但rbm生成的形状模糊，并且丢失了马的许多信息，比如腿、尾巴，而crbm则较好的保留了马的信息。

对于训练集，rbm采样生成的形状的平均欧氏距离是7.9422，crbm模型生成形状的平均欧氏距离是5.3751；对于测试集，rbm采样生成的形状的平均欧氏距离是8.4669，crbm模型生成形状的平均欧氏距离是5.9178。在有噪声干扰的情况下，无论是训练集还是测试集，二者生成形状的时间相差不多，但欧氏距离度量值表明crbm模型生成的形状与原始目标更相近，建模形状的效果更好。

训练集和测试集图像添加均值为0、方差为0.04的高斯噪声作为输入。得到的结果如附图9所示。

附图9只是展示了训练集和测试集中的五幅图像。附图9中(a)和(b)分别表示训练集和测试集中的图像添加噪声之后的采样生成形状的结果，其中(a)列表示的是原始的未添加噪声的图像，(b)列表示的是对(a)列中的图像添加噪声，(c)列和(d)列分别表示的是rbm和crbm采样生成形状的结果图。从附图9中可以直观的看出，无论是训练集还是测试集中的图像，这两个模型都能有效的去除噪声影响，但是crbm生成的形状比rbm清晰，几乎没有丢失马的信息。

对于训练集，rbm采样生成的形状的平均欧氏距离是8.0513，crbm模型生成形状的平均欧氏距离是4.5100；对于测试集，rbm采样生成的形状的平均欧氏距离是8.6654，crbm模型生成形状的平均欧氏距离是4.9574。欧氏距离度量值表明crbm建模形状的效果比较好。

需要说明的是，在本发明中，诸如第一和第二等之类的关系术语仅仅用来将一个实体或者操作与另一个实体或操作区分开来，而不一定要求或者暗示这些实体或操作之间存在任何这种实际的关系或者顺序。而且，术语“包括”、“包含”或者其任何其他变体意在涵盖非排他性的包含，从而使得包括一系列要素的过程、方法、物品或者装置不仅包括那些要素，而且还包括没有明确列出的其他要素，或者是还包括为这种过程、方法、物品或者装置所固有的要素。在没有更多限制的情况下，由语句“包括一个……”限定的要素，并不排除在包括所述要素的过程、方法、物品或者装置中还存在另外的相同要素。

本说明书中的各个实施例均采用相关的方式描述，各个实施例之间相同相似的部分互相参见即可，每个实施例重点说明的都是与其他实施例的不同之处。

尤其，对于装置实施例而言，由于其基本相似于方法实施例，所以描述的比较简单，相关之处参见方法实施例的部分说明即可。

在流程图中表示或在此以其他方式描述的逻辑和/或步骤，例如，可以被认为是用于实现逻辑功能的可执行指令的定序列表，可以具体实现在任何计算机可读介质中，以供指令执行系统、装置或设备(如基于计算机的系统、包括处理器的系统或其他可以从指令执行系统、装置或设备取指令并执行指令的系统)使用，或结合这些指令执行系统、装置或设备而使用。就本说明书而言，″计算机可读介质″可以是任何可以包含、存储、通信、传播或传输程序以供指令执行系统、装置或设备或结合这些指令执行系统、装置或设备而使用的装置。计算机可读介质的更具体的示例(非穷尽性列表)包括以下：具有一个或多个布线的电连接部(电子装置)，便携式计算机盘盒(磁装置)，随机存取存储器(ram)，只读存储器(rom)，可擦除可编辑只读存储器(eprom或闪速存储器)，光纤装置，以及便携式光盘只读存储器(cdrom)。另外，计算机可读介质甚至可以是可在其上打印所述程序的纸或其他合适的介质，因为可以例如通过对纸或其他介质进行光学扫描，接着进行编辑、解译或必要时以其他合适方式进行处理来以电子方式获得所述程序，然后将其存储在计算机存储器中。

应当理解，本发明的各部分可以用硬件、软件、固件或它们的组合来实现。

在上述实施方式中，多个步骤或方法可以用存储在存储器中且由合适的指令执行系统执行的软件或固件来实现。例如，如果用硬件来实现，和在另一实施方式中一样，可用本领域公知的下列技术中的任一项或他们的组合来实现：具有用于对数据信号实现逻辑功能的逻辑门电路的离散逻辑电路，具有合适的组合逻辑门电路的专用集成电路，可编程门阵列(pga)，现场可编程门阵列(fpga)等。

以上所述，仅为本发明的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到的变化或替换，都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应以权利要求的保护范围为准。