一种变权重系数的并网光伏电站短期功率组合预测方法与流程

本发明涉及新能源发电与电力系统技术领域，尤其是涉及一种变权重系数的并网光伏电站短期功率组合预测方法。

背景技术：

近年来，太阳能开发利用规模快速扩大，技术进步和产业升级加快，成本显著降低，已成为全球能源转型的重要领域。“十二五”时期，我国光伏产业体系不断完善，技术进步显著，光伏制造和应用规模均居世界前列。太阳能热发电技术研发及装备制造取得较大进展，已建成商业化试验电站，初步具备了规模化发展条件。截止到2014年底，光伏发电累计装机容量2805万千瓦，提前完成“十二五”规划目标，表明我国光伏市场蕴藏了巨大的发展潜力。

“十三五”将是太阳能产业发展的关键时期，基本任务是产业升级、降低成本、扩大应用，实现不依赖国家补贴的市场化自我持续发展，成为实现2020年和2030年非化石能源分别占一次能源消费比重15％和20％目标的重要力量。截至2016年底，我国光伏发电新增装机容量3454万千瓦，累计装机容量7742万千瓦，新增和累计装机容量均为全球第一。其中，光伏电站累计装机容量6710万千瓦，分布式累计装机容量1032万千瓦。全年发电量662亿千瓦时，占我国全年总发电量的1％。由于光伏电站的出力易受气象环境因素的影响，具有不确定性和不稳定性等特点，随着光伏并网渗透率的不断提高，必将会对电力系统的安全稳定运行产生一定影响，所以迫切需要对光伏电站在未来一段时间内的输出功率进行准确预测。而对于目前常见的单一预测模型来讲，提高其预测精度的难度较大，且各单一预测模型的准确度和适用性有所不同，预测存在不确定性。概率是一种表达不确定性的方式，而组合预测(或集合预报)则是获得概率预报的一个有效途径。

目前对于分析影响光伏出力的气象因素的研究上，由于影响光伏电站出力的气象因素复杂多变，实际的天气变化情况也复杂得多，且难以对与光伏出力相关的气象因素进行全面分析，目前常见的光伏预测模型大多是以考虑少量的气象因素，如以太阳辐照度和气温等为输入变量，而很少考虑引入大气清晰度指数、日照时数、温差等相关环境影响因素。即使在建模时将上述气象因素全部考虑在内，同样会增加预测模型的复杂性，况且各气象因素之间也是存在多重共线性关系，不利于预测模型的建立，所以在建立预测模型时所选取的气象环境要素及如何降低气象因素间的多重共线性关系对于模型预测精度的提高显得尤其重要。

在建立模型时除了上述所考虑的气象因素条件以外，模型算法的选取对于预测精度来说同样重要，已往对于光伏电站功率预测多是以单一预测模型为主，而对于单一预测模型，提高其预测精度的难度较大，且各单一预测模型的准确度和适用性有所不同，预测存在不确定性。

目前常见的组合预测一般是对多种单一预测模型所得到的预测结果进行的一种组合，但是不同的单一模型的预测结果肯定是各不相同的，这就需要对各单一预测模型的输出结果确定一个权值，等权重的预测模型由于单一预测模型预测结果的权重相同，这就会由于某个单一预测模型的预测结果出现较大偏差，影响组合预测模型的预测结果，选取适当权重的主要目的在于消除单一预测方法可能存在的较大偏差，提高预测的准确性。

鉴于以上原因，传统的光伏功率预测方法难以满足光伏电站和电力系统实用、简单以及预测能力的要求。

技术实现要素：

本发明的目的就是为了克服上述现有技术存在的缺陷而提供一种更准确的变权重系数的并网光伏电站短期功率组合预测方法。

本发明的目的可以通过以下技术方案来实现：

一种变权重系数的并网光伏电站短期功率组合预测方法，该方法的步骤包括：

s1、利用包含离预测时段最近的历史数据建立多种单一预测模型，求出各个单一预测模型对预测样本点的拟合值；

s2、通过灰色关联分析法计算各个单一预测模型在每个预测样本点的权重系数；

s3、利用步骤s1和步骤s2分别得到的各个单一预测模型对每个预测样本点的拟合值和对应的权重系数训练拟合得到bpnn网络模型；

s4、通过预测时段最新气象要素预测值得到各个单一预测模型的单一功率预测值，然后利用步骤s3得到的bpnn网络模型计算出各个单一预测模型在预测时段的时变权重系数，利用得到的单一功率预测值和时变权重系数计算出预测时段的功率预测值；

s5、循环步骤s1～s4，不断更新预测时段的功率预测值。

所述步骤s1具体包括：

s11、获取光伏电站离预测时段最近的历史气象要素数据和历史光伏输出功率数据作为样本数据，所述样本数据包括训练样本和预测样本；

s12、利用步骤s11得到的训练样本数据，通过最小化训练误差进行训练拟合，建立多种单一预测模型，求出各个单一预测模型对预测样本的拟合值。

所述步骤s2具体包括：通过灰色关联分析法计算各个单一预测模型在预测样本点处的拟合值与观测值间的灰色关联系数，将得到的灰色关联系数作为对应单一预测模型的权重系数。

所述步骤s3具体包括：将步骤s1得到的各个单一预测模型对每个预测样本点的拟合值作为输入，将步骤s2得到的各个单一预测模型对应的权重系数作为输出，训练得到bpnn网络模型。

所述步骤s4具体包括：

s41、获取预测时段最新的气象要素预测值；

s42、利用步骤s41得到的最新气象要素预测值计算出各个单一预测模型对预测时段的单一功率预测值；

s43、将步骤s42得到的单一功率预测值输入步骤s3得到的bpnn网络模型中，得到各个单一预测模型在预测时段的时变权重系数；

s44、对于每个预测时段，将各个单一预测模型得到的单一功率预测值乘以对应的时变权重系数后再全部叠加，得到该预测时段的功率预测值。

所述多种单一预测模型包括：支持向量机模型、灰色关联分析结合支持向量机模型以及主成分分析结合支持向量机模型。

所述气象要素包括：小时水平面上太阳总辐射、小时地外水平面总辐射、日照时数、小时平均气温、小时最高气温、小时最低气温、相对湿度、本站气压和风速。

与现有技术相比，本发明具有以下优点：

1、将多种影响光伏电站输出功率的气象因素考虑在内，分别依据主成分分析法和灰色关联分析法对气象因素进行降维处理，减少了单一预测模型中考虑的气象因素个数，综合考虑气象因素的同时简化了传统单一预测模型的复杂程度。

2、由于气候因素的不确定性，光伏功率预测不可避免地存在不确定性，概率是一种表达不确定性的方式，而组合预测或集合预报则是获得概率预报的一个有效途径，本发明提出的组合预测的思想，不仅符合气象科学和光伏发电的实际，也有利于电力系统调峰和电网规划。

3、将灰色关联系数作为组合预测中各种单一预测模型的权值，再通过bpnn网络模型建立时变权重系数组合预测模型，实现不同单一预测模型在不同预测时间节点处不同权重系数的变化，能够弥补单一预测模型预测误差大的缺点，降低了预测模型出现极端误差的概率，提高了模型的预测精度。

4、该组合预测模型的算法结构简单，bpnn网络模型建立完成后，只需要输入单一预测模型的预测值就能得到时变权重系数，能高效满足对光伏电站输出功率的预测要求。

附图说明

图1为本发明变权重系数的并网光伏电站短期功率组合预测方法流程图；

图2为本发明方法逻辑示意图；

图3为本发明模型建立过程示意图；

图4为功率观测值与3种单一预测模型的功率预测值的曲线图；

图5为svm模型的预测结果残差误差直方图；

图6为gra-svm模型的预测结果残差误差直方图；

图7为pca-svm模型的预测结果残差误差直方图；

图8为本发明变权重系数组合预测模型的功率预测值与观测值的曲线图；

图9为本发明变权重系数组合预测模型的预测结果残差误差直方图。

具体实施方式

下面结合附图和具体实施例对本发明进行详细说明。本实施例以本发明技术方案为前提进行实施，给出了详细的实施方式和具体的操作过程，但本发明的保护范围不限于下述的实施例。

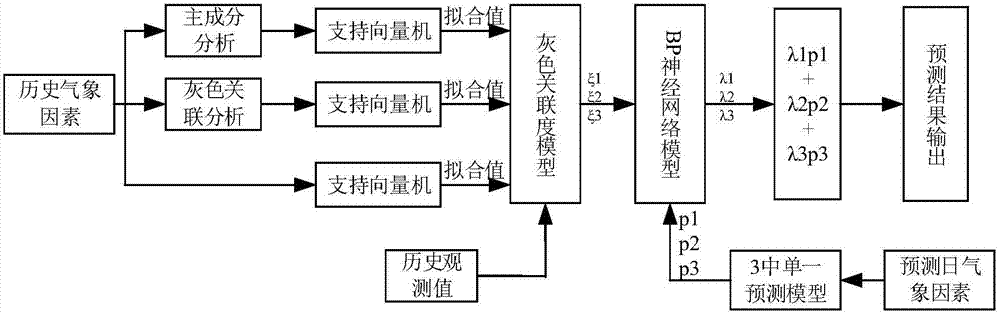
本方法在已经建立完成的单一预测模型以及等权重预测模型的基础上，提出一种变权重系数组合预测模型实现对光伏电站输出功率的预测，能对多种单一预测模型的权重系数进行实时调整。提出的方法通过灰色关联分析结合bp神经网络得到变权重系数组合模型，实现了用支持向量机模型(svm)、灰色关联分析结合支持向量机模型(gra-svm)和主成分分析结合支持向量机模型(pca-svm)三种单一预测模型在不同预测时间点权重系数变化的功率预测。首先根据历史气象要素数据和光伏功率观测值建立svm、gra-svm和pca-svm三种单一预测模型，利用灰色关联分析得出三种单一预测模型的权重系数，然后根据求出的权重系数结合三种单一预测模型的拟合值训练建立bp神经网络模型；根据最新的气象要素预测值求出三种单一预测模型的单一功率预测值，通过建立的bp神经网络模型计算单一预测模型的时变权重系数，叠加乘以时变权重系数后的单一功率预测值，得到最终功率预测值。

如图1～3所示，一种变权重系数的并网光伏电站短期功率组合预测方法，该方法的步骤包括：

s1、利用包含离预测时段最近的历史数据建立多种单一预测模型，求出各个单一预测模型对预测样本点的拟合值，具体包括以下步骤：

s11、数据的获取及预处理：

获取光伏电站离预测时段最近的历史气象要素数据和历史光伏输出功率数据作为样本数据，气象要素包括小时水平面上太阳总辐射、小时地外水平面总辐射(天文辐射)、日照时数、小时平均气温、小时最高气温、小时最低气温、相对湿度、本站气压和风速，根据所获取的气象要素数据计算出小时温差、清晰度指数等，对获取的数据进行标准化处理，样本数据包括训练样本和预测样本；

s12、利用步骤s11得到的训练样本数据，通过最小化训练误差进行训练拟合，建立3种单一预测模型，求出各个单一预测模型对预测样本的拟合值：

s121、建立svm模型：

支持向量机回归是一种智能机器学习算法，被应用于解决非线性回归问题，这种统计学习算法是基于结构风险最小化为原则，可以在较少的样本情况下，实现理想的拟合效果，目前，在并网光伏电站输出功率预测问题上，存在电站历史输出功率数据不足及气象资料不全面等问题，选取支持向量机模型作为单一预测模型用于光伏出力预测十分合适；

s122、建立gra-svm模型：依据灰色关联理论，计算历史气象数据的各气象因素与光伏输出功率之间关联度的大小，本实施例中，选取前5个关联度值较大的气象因素作为支持向量机的模型输入；

s123、建立pca-svm模型：根据主成分分析理论，本实施例中，对8个原始气象变量进行降维处理，综合得出3个主成分因子量作为支持向量机模型的输入；

s2、通过灰色关联分析法计算各个单一预测模型在预测样本点处的拟合值与观测值间的灰色关联系数，将得到的灰色关联系数作为对应单一预测模型的权重系数；设第v个预测模型在第w个预测样本点处拟合值pv(w)与观测值间的灰色关联系数ξv(w)，在本实施例中，组合预测模型在预测样本集第w个时段的拟合值为：

p(w)＝ξ1(w)p1(w)+ξ2(w)p2(w)+ξ3(w)p3(w)；

s3、将步骤s1得到的各个单一预测模型对每个预测样本点的拟合值作为输入，将步骤s2得到的各个单一预测模型对应的权重系数作为输出，训练得到bpnn网络模型；

s4、通过预测时段最新气象要素预测值计算出预测时段的功率预测值：

s41、获取预测时段最新的气象要素预测值；

s42、利用步骤s41得到的最新气象要素预测值计算出各个单一预测模型对预测时段的单一功率预测值pv；

s43、将步骤s42得到的单一功率预测值输入步骤s3得到的bpnn网络模型中，得到各个单一预测模型在预测时段的时变权重系数λv；

s44、对于每个预测时段，将各个单一预测模型得到的单一功率预测值乘以对应的时变权重系数后再全部叠加建立变权重系数组合预测模型，得到该预测时段的功率预测值：

p＝λ1p1+λ2p2+λ3p3；

s5、循环步骤s1～s4，不断更新预测时段的功率预测值。

上述步骤s2中灰色关联系数的具体计算步骤进一步分析如下：

s21、参考序列与比较序列的选择：

首先设x为灰色系统因子集，有xi∈x为系统要素。xi序列的第k个数据点表示为xi(k)，其中k＝1,2,3……,n，n为要素样本数据个数。定义系统要素的参考序列为x0＝{x0(1),x0(2),x0(3),…,x0(n)}；

其它列入指标体系表中的指标组成的序列即为比较序列，记为xi：

xi＝{xi(1),xi(2),xi(3),…,xi(n)}

其中，i＝1,2,3,…,m，m为比较序列的个数；

选取光伏电站输出功率为参考序列，气象因素为比较序列，进行气象因素与光伏电站输出功率之间灰色关联系数的计算；

s22、无量纲化处理：

为了消除由于各序列之间量纲不统一而对灰色关联分析结果产生的影响，需要对输入的各气象序列数据进行处理，剔除奇异和不完整的数据，并对其余数据进行归一化处理，归一化公式如下所示：

式中，xmax、xmin分别为指定序列中的最大值和最小值；

s23、计算灰色关联系数：

利用下式计算气象因素比较序列的各指标对应于输出功率参考序列各指标的关联系数：

式中，ρ为分辨系数，在0～1之间变化，一般取ρ为0.5，分辨系数的不确定会导致关联系数计算结果的不稳定，分辨系数ρ取不同的值可能造成各个比较序列与参考序列灰色关联度的序位发生改变；

s24、灰色关联度计算：

由于关联系数ξi(k)数目较多，不便于比较，因此将数列xi与参考序列x0各点的关联系数相加取平均值：

由ri依次排成的数列为关联序列，根据排位次序即可确定各比较数列对参考数列影响程度的重要性。

由公式(3)可知，灰色关联度ri通常取值范围为0～1，其值越接近1，表明比较序列对参考序列的影响越大。

表1为利用灰色关联理论计算所得出的气象变量与光伏电站输出功率之间的灰色关联度的值，对气象变量与功率间的灰色关联度进行排序有：r(总辐射量)>r(清晰度指数)>r(风速)>r(日照时数)>r(小时平均温度)>r(小时温差)>r(本站气压)>r(相对湿度)。本实施例选取与电站输出功率关联度较大的前5个气象变量作为支持向量机模型的输入，构造gra-svm模型进行预测。

表1气象因素与光伏电站输出功率间灰色关联度

上述步骤s123中主成分分析的步骤具体包括：

s1231、将原有气象变量数据进行标准化处理：

设原有变量有s个，分别用x1,x2,x3,…,xs表示，将原有变量进行标准化处理，标准化公式为：

式中，x^*lj表示第j个变量在第l个样本处标准化后的结果，xlj为第j个变量在第l个样本处的数据值，sj分别为第j个变量的均值和方差；

s1232、计算变量的简单相关系数矩阵r：

r＝y^ty(n-1)

其中，y为原始变量标准化后的矩阵，n为变量的样本个数；

s1233、计算相关系数矩阵r的特征值δ1≥δ2≥δ3≥…≥δs≥0及对应的单位特征向量μ1,μ2,μ3,…,μs。

s1234、确定所选取主成分个数：

第q个因子的方差贡献率为：

前t个因子的累计方差贡献率为：

因子累计方差贡献率反应前t个因子对原有变量信息的解释程度，一般地，所选取的主成分因子的数量取决于因子累计方差贡献率，当累计方差贡献率大于75％～85％，说明所提取的因子个数可以反应原有变量的大部分信息。

表2所示为根据相关系数矩阵计算得出的不同气象因素的30天的所有主成分因子的特征值及方差贡献值，可见前3个主因子的累计方差贡献率为81.89％，所以选择提取前3个主成分因子足以代替原有气象变量的大部分信息；

表2因子累计方差贡献表

通过上述步骤，计算便得到各个主成分，表3所示为前3个主成分得分系数矩阵，得分系数的绝对值大小表明该变量对相应主成分的贡献程度大小。其中，p表示日平均气压，kt表示清晰度指数，h表示水平面上太阳总辐射，td表示气温日较差，t表示日平均气温，s表示日照时数，rr表示相对湿度，v表示风速。其中的前t个特征值和对应的特征向量便是因子分析的初始解。然后将其计算得出的主成分因子值作为svm的输入进行训练拟合，构造pca-svm模型进行预测。

表3成份得分系数矩阵

图4表示3种单一预测模型的预测结果曲线与实际观测值的曲线，可见，单一预测模型的预测曲线基本与光伏电站实际观测值曲线相一致，但是模型在某些预测时间点与观测值相差较大，如gra-svm模型在5月9日12时的预测结果与观测值相差甚远。

图5～7分别表示3种单一预测模型的预测结果残差误差直方图。如图5所示，svm模型的残差主要集中分布在两侧-0.2～-0.1和0.1～0.3之间，在-0.1到0.1区间几乎无分布；如图6所示，gra-svm模型的残差误差分布范围较大，且在大于正方向0.5处仍有分布，说明模型预测结果存在出现极端残差误差的可能性，这也导致模型的me误差较大；如图7所示，pca-svm模型的残差分布范围虽然相对较小，但也主要是集中在两侧-0.3～-0.1和0.1～0.3区间，且直方图分布的左右比较对称，这使得其模型的me计算误差较小。从3个单一预测模型的me误差及残差误差直方图分布的整体来看，pca-svm模型的预测结果偏差相对最小，利用pca对气象变量进行处理，降低了svm网络模型的输入量，简化模型复杂度，svm模型预测结果偏差次之，gra-svm模型预测结果偏差相对最大，这可能是由于在gra-svm经过筛选后，仅选择对光伏输出影响较大的5个气象变量作为输入，使gra-svm模型的预测精度有所降低。

图8所示为本方法提出的变权重系数组合预测模型与观测值的曲线，从图中可以看出，变权重系数组合预测模型预测结果的曲线与观测值曲线相近。

图9所示为本方法提出的变权重系数组合预测模型的预测结果残差误差直方图，组合模型的残差误差直方图左偏，且残差误差主要集中在-0.1～0.1之间，但是模型的预测结果出现较大的残差误差是小概率事件。

以上试验结果均表明：本方法可以比单一预测模型实现更加准确的并网光伏电站短期出力的预测。