适用于非正定型相关性控制的改进拉丁超立方抽样方法与流程

本发明涉及一种拉丁超立方抽样方法，具体涉及配电网仿真计算中适用于非正定型相关性控制的改进拉丁超立方抽样技术，属于分布式电源接入后的电力系统配电网随机潮流采样仿真技术领域。

背景技术：

基于光伏、风力等可再生能源的分布式发电技术，能够有效地缓解能源紧张、环境污染等问题，得到了广泛的应用。但是配电网的潮流分布会受到分布式电源并网运行的影响。光伏发电和风力发电的输出功率由于自然环境因素的影响具有较强的随机性。当分布式电源采取多点并网时，多个电源之间的相关性问题也需要考虑。例如实际中光伏出力由于同地域光照的强相关性往往呈现正相关。同理，分布式风电中相邻风机一般也呈现正相关。风光由于夜晚风大、白天风小呈现互补性，即负相关。

模拟法是计算随机潮流的有效方法，拉丁超立方抽样法作为改进的模拟法，通过分层抽样，使得样本点均匀、全面地覆盖到变量的分布范围，有效地减小方差，拉丁超立方抽样法包括抽样和相关性控制两个部分。目前抽样方法主要包括区间随机抽样、点阵抽样和重要抽样等。但是这些方法都要求已知输入变量的累积分布函数，无法解决cdf较难准确获得或未知的情况。相关性控制的方法主要包括：遗传算法、模拟退火算法和cholesky分解。cholesky分解，计算简便速度快，但仅适用于相关系数矩阵为正定矩阵的情况。一般在相关性控制中将相关系数矩阵处理为正定矩阵。但随着分布式电源并网规模的增加，矩阵的维数增加，正定的可能性大大降低，这种处理方式不再合适。因此本发明提出一种基于修正相关系数矩阵的改进拉丁超立方抽样法。有效解决了输入变量分布函数未知和非正定矩阵无法分解的问题，扩大了拉丁超立方抽样法的适用范围。

技术实现要素：

本发明正是针对现有技术中存在的技术问题，提供一种适用于非正定型相关性控制的改进拉丁超立方抽样方法，该方法解决了输入变量的累积分布函数较难准确获得或未知的情况，以及相关性控制中非正定矩阵无法cholesky分解的问题，扩大了拉丁超立方抽样法的适用范围。

为了解决上述技术问题，本发明的技术方案如下：一种适用于非正定型相关性控制的改进拉丁超立方抽样方法，包括：

步骤s1，首先获得输入变量的累积分布函数或输入变量大量实测的离散数据及各变量间的相关系数矩阵；

步骤s2，分布函数已知时采用重要抽样法抽取样本，未知时采用改进的拉丁超立方抽样法抽取样本，得到样本矩阵；

步骤s3，基于正定谱分解法，对相关系数矩阵进行修正；

步骤s4，对修正后的随机顺序矩阵的相关系数矩阵，进行cholesky分解和相关变换；

步骤s5，对指定的相关系数矩阵修正分解后确定最终的顺序矩阵，按顺序矩阵排序，确定最终的样本矩阵；

步骤s6，将样本矩阵带入节点，进行潮流计算,得到节点电压与支路功率，计算相对误差指标。

进一步地，所述步骤s1中具体为：确定各节点接入的新能源类型，当输入变量的累积分布函数已知时，建立输出功率的模型，确定输入变量的累积分布函数；当输入变量的累积分布函数无法准确获得或者未知时，获取该变量大量实测的离散数据，计算各变量间的相关系数矩阵。

进一步地，所述步骤s2中具体为：分布函数已知时采用重要抽样法抽取样本，抽样公式为：分布函数未知时采用改进的拉丁超立方抽样法抽取样本，步骤为：对每个变量的m个离散样本数据按照从小到大排序，得到排序后的矩阵t'n×m；将累积分布函数的取值范围其均匀分为a等份；t”n×m即为抽样后的样本，t”k,a计算公式：t”k,a＝t'k,jj＝round((a·m)/a)。

进一步地，所述步骤s3中具体为：所述步骤s3具体为：基于正定谱分解法，对相关系数矩阵进行修正，修正步骤为：求得非正定矩阵c的特征值与特征向量后，重新定义对角矩阵λ'，根据变换后得到修正矩阵c',具体步骤如下：1)c为n阶方阵，λi与列向量si为它的一个特征值与相应的特征向量,满足：

csi＝λisi

si＝[si1,si2,...sin]^t；

2)选取一个很小的正值ε(取值将影响误差大小，为保证算法的精度，一般小于10^-4)，将对角矩阵λ重新定义为对角矩阵λ'：

λ＝diag(λi)

3)根据特征向量矩阵s，定义对角标度矩阵t：

4)根据变换得到修正矩阵c':

c'＝bb^t

c'即为修正后的正定矩阵。

进一步地，所述步骤s4中具体为：用改进的spearman秩相关系数，用样本顺序代替样本值，进行相关性控制，对修正后的随机顺序矩阵相关系数矩阵进行cholesky分解，得到下三角矩阵，变换后得到d，将初始样本中参照d排序，此时的相关性大大减小。

进一步地，所述步骤s5中具体为：对指定的相关系数矩阵pset修正分解，得到下三角矩阵qset，再对d变换：dset＝qsetd，求得dset；将顺序矩阵的每一行元素按照dset中的每一行元素重新排序，确定最终的顺序矩阵，按顺序矩阵排序，确定最终的样本矩阵。

进一步地，所述步骤s6中具体为：将样本矩阵代入节点，进行随机潮流计算，得到各节点电压与支路功率，得出分布情况，根据计算相对误差指标。

相对于现有技术，本发明的有益效果如下：1)本发明提供的一种适用于非正定型相关性控制的改进拉丁超立方抽样方法，以变量的离散数据为基础改进抽样方法，解决了输入变量分布函数未知的问题，基于正定谱分解法，通过对相关系数矩阵进行简单的变换修正，克服了非正定矩阵无法分解的问题，仿真证明修正后的矩阵为正定矩阵，均可进行cholesky分解，计算速度快且误差较小；该方法由仅适用于分布函数已知推广到分布函数未知，由仅适用于正定推广到非正定，扩大了拉丁超立方采样法的适用范围；2)本发明提供的一种适用于非正定型相关性控制的改进拉丁超立方抽样方法，该算法得到输出功率的样本的准确性和收敛性要优于蒙特卡罗模拟法。通过电压、功率等输出变量的误差分析，可以看出在随机潮流的计算中，该算法的准确性和收敛性都要优于蒙特卡罗模拟法；相同计算精度下需要的规模和时间远小于蒙特卡罗模拟法。

附图说明

图1为本发明所述的改进拉丁超立方抽样方法的流程图；

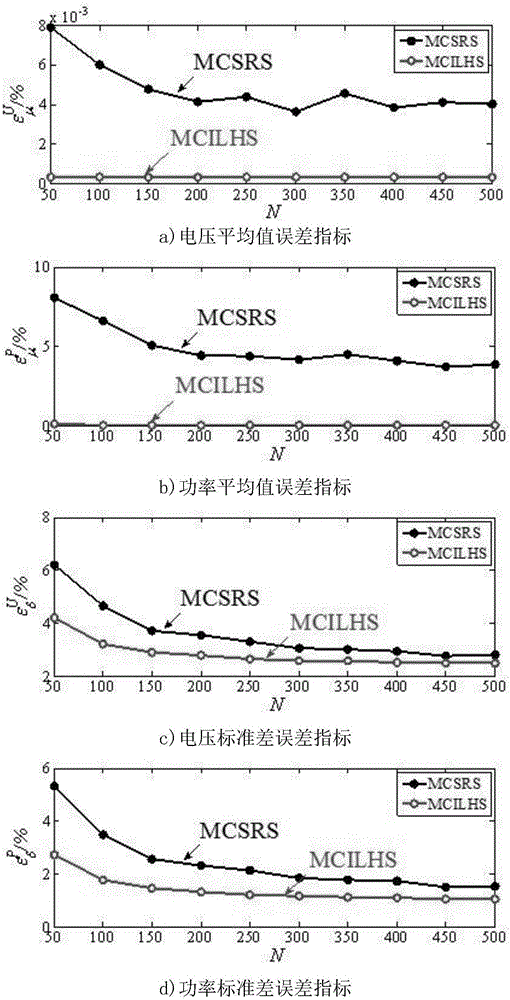
图2所示为本发明实施案例一中两种算法下69节点输出变量的相对误差指标；

其中：mcsrs表示蒙特卡罗模拟法，mcilhs表示拉丁超立方抽样法。

具体实施方式

本发明提供一种适用于非正定型相关性控制的改进拉丁超立方抽样方法，其方法流程如图1所示，由图1可知，该方法包括：

步骤s1，首先获得输入变量的累积分布函数或输入变量大量实测的离散数据及各变量间的相关系数矩阵；

步骤s2，分布函数已知时采用重要抽样法抽取样本，未知时采用改进的拉丁超立方抽样法抽取样本，得到样本矩阵；

步骤s3，基于正定谱分解法，对相关系数矩阵进行修正；

步骤s4，对修正后的随机顺序矩阵的相关系数矩阵，进行cholesky分解和相关变换；

步骤s5，对指定的相关系数矩阵修正分解后确定最终的顺序矩阵，按顺序矩阵排序，确定最终的样本矩阵；

步骤s6，将样本矩阵带入节点，进行潮流计算,得到节点电压与支路功率，计算相对误差指标。

所述步骤s1中具体为：确定各节点接入的新能源类型，当输入变量的累积分布函数已知时，建立输出功率的模型，确定输入变量的累积分布函数；当输入变量的累积分布函数无法准确获得或者未知时，获取该变量大量实测的离散数据，计算各变量间的相关系数矩阵。

所述步骤s2中具体为：分布函数已知时采用重要抽样法抽取样本，抽样公式为：分布函数未知时采用改进的拉丁超立方抽样法抽取样本，步骤为：对每个变量的m个离散样本数据按照从小到大排序，得到排序后的矩阵t'n×m；将累积分布函数的取值范围其均匀分为a等份；t”n×m即为抽样后的样本，t”k,a计算公式：t”k,a＝t'k,jj＝round((a·m)/a)。

所述步骤s3中具体为：所述步骤s3具体为：基于正定谱分解法，对相关系数矩阵进行修正，修正步骤为：求得非正定矩阵c的特征值与特征向量后，重新定义对角矩阵λ'，根据变换后得到修正矩阵c',具体步骤如下：1)c为n阶方阵，λi与列向量si为它的一个特征值与相应的特征向量,满足：

csi＝λisi

si＝[si1,si2,...sin]^t；

2)选取一个很小的正值ε(取值将影响误差大小，为保证算法的精度，一般小于10^-4)，将对角矩阵λ重新定义为对角矩阵λ'：

λ＝diag(λi)

3)根据特征向量矩阵s，定义对角标度矩阵t：

4)根据变换得到修正矩阵c':

c'＝bb^t

c'即为修正后的正定矩阵。

所述步骤s4中具体为：用改进的spearman秩相关系数，用样本顺序代替样本值，进行相关性控制，对修正后的随机顺序矩阵相关系数矩阵进行cholesky分解，得到下三角矩阵，变换后得到d，将初始样本中参照d排序，此时的相关性大大减小。

所述步骤s5中具体为：对指定的相关系数矩阵pset修正分解，得到下三角矩阵qset，再对d变换：dset＝qsetd，求得dset；将顺序矩阵的每一行元素按照dset中的每一行元素重新排序，确定最终的顺序矩阵，按顺序矩阵排序，确定最终的样本矩阵。

所述步骤s6中具体为：将样本矩阵代入节点，进行随机潮流计算，得到各节点电压与支路功率，得出分布情况，根据计算相对误差指标。

实施例1：

本发明提供一种适用于非正定型相关性控制的改进拉丁超立方抽样方法的实施案例中：

步骤s1中累积分布函数和离散数据矩阵的确定包括：

在pg&e69节点系统的5个节点接入分布式电源。以光伏为例，光伏模型采用beta分布模型，形状参数的选取为：α＝0.9,β＝0.85，容量为100kva。确定输入变量的累积分布函数为5个光伏输出功率样本之间的相关系数矩阵为p5。

步骤s2中分布函数已知时采用重要抽样法抽取样本包括：

抽样原理第k个变量第a个值为：当x＝xka时，zk(xka)具有中的最大值。

步骤s3中基于正定谱分解法，对相关系数矩阵进行修正包括：

c为n阶方阵，λi与列向量si为它的一个特征值与相应的特征向量。选取一个很小的正值ε，将对角矩阵λ重新定义为对角矩阵λ'：λ':

根据特征向量矩阵s，定义对角标度矩阵t：t:

根据变换得到修正矩阵c':c'＝bb^t,

修正误差有关于所有元素和特征值两种：

修正前后的相关系数矩阵和误差为：

步骤s4中对修正后的随机顺序矩阵的相关系数矩阵，进行cholesky分解和相关变换包括：

对输入变量x1,x2,…,xn按照分布情况抽样，规模为1*m，得到样本矩阵fn*m。生成随机的顺序矩阵an*m，求出an*m的相关系数矩阵pa，对pa进行cholesky分解，得下三角矩阵q，按d＝q^-1a对顺序矩阵进行变换。将初始样本fn*m中的各行元素参照d中对应的各行元素大小重新排序，求出fd。此时fd的相关性削弱。

步骤s5中对指定的相关系数矩阵修正分解后确定最终的顺序矩阵，按顺序矩阵排序，确定最终的样本矩阵包括：

当输入变量间需要达到必要的相关系数时，令指定的相关系数矩阵为pset，对pset进行cholesky分解，得到下三角矩阵qset。dset＝qsetd，求得dset；将顺序矩阵a的每一行元素按照dset中的每一行元素重新排序，得到新的顺序矩阵aset，将初始样本f按aset排序，得到fset，fset的相关系数满足设定的要求。

步骤s6中将样本矩阵带入节点，进行潮流计算,得到节点电压与支路功率，计算相对误差指标包括：

样本拟合的效果用相对误差指标来表示，计算公式为：

c表示形状参数α,β，cb表示给定值。

为表示计算精确度，用平均值与标准差的相对误差指标计算，公式如下：

u表示电压，与之对应的是功率p。为选取的电压的基准值。图2为本发明实施案例一中两种算法下69节点输出变量的相对误差指标。

以上对本申请进行了详细介绍，本文中应用了具体个例对本申请的原理及实施方式进行了阐释，以上实施例的说明只是用于帮助理解本申请的方法及核心思想，在具体实施方式及应用范围上均会有改变之处，综上所述，本说明不应理解为对本申请的限制。