基于轮廓的猪只饮水行为识别方法与流程
本发明涉及机器视觉技术与模式识别技术,具体涉及一种俯视状态下群养猪监控视频中猪只饮水行为识别方法。
背景技术:
随着农业改革以及现代养猪技术的逐步引入,养猪业在规模化和智能化方面都已经有所提高,探讨基于机器视觉的俯视群养猪视频序列中猪个体行为研究等已经越来越受到国内外学者的关注。对于猪个体的行为识别,目前广泛使用的方法是耳标rfid,现阶段采用计算机视觉技术监测猪只饮水行为的研究少有相关报道,考虑到机器视觉算法在猪只其他行为的应用,对于饮水行为的识别成为发展的趋势。本发明给出了一种基于轮廓的猪只饮水行为识别方法,为今后对群养猪采食、排便等行为的识别研究打下了基础。
技术实现要素:
本发明的目的是对俯视状态下群养猪监控视频中猪只饮水行为进行识别,为此提出一种基于轮廓的猪只饮水行为识别方法。
本发明采用的技术方案是:基于轮廓的猪只饮水行为识别方法,包括以下步骤:
(1)获取俯视状态下群养猪视频,然后进行图像预处理,主要是饮水区域内猪个体目标的提取,样本库的建立;(2)将任一曲线看作为一系列点的集合,逐步减少点的数量,达到简化曲线的目的;经过多次化简,保留其中满足条件的坐标点,从而去掉了其他对曲线影响相对较弱的点,对猪个体的轮廓进行多边形拟合;(3)针对近似得到的多边形,提取具有代表性的多边形的轮廓特征;(4)计算两个多边形之间的相似度,从而完成轮廓的匹配。
进一步,所述步骤(1)具体包括改建实验用猪舍,在猪舍正上方安装拍摄俯视视频的图像采集系统,获取俯视群养猪彩色视频片段,选取符合条件的视频帧,提取饮水区域内猪个体目标和建立样本库。
进一步,所述步骤(1)中猪个体目标提取的具体方法是,对单帧图像采用改进的二维otsu图像算法进行分割,接着对分割结果做数学形态学处理,得到饮水区域内的猪个体轮廓图像。
进一步,所述步骤(3)中多边形的轮廓特征提取,该过程是对近似多边形所保留的点建立特征量的一个过程,采用角度和距离来构建二维特征量pij=(dij,θij);根据其在离散空间的分布情况,将距离和角度离散化,建立任一基向量
进一步,所述步骤(4)中基于多边形特征的轮廓匹配,首先要求基线段具有相似的描述子,利用匈牙利算法得到代价最小的最优匹配,得到轮廓基向量之间的最优匹配关系;其次匹配代价公式,当最优匹配下的基向量之间的代价值小于某个阈值t时,就认为该基向量匹配正确,最后计算待匹配轮廓上正确匹配的基向量个数和样本库中的训练样本轮廓上基向量的总数的比值,该比值越大表明相似程度越高,反之越低,从而得到两个轮廓之间的相似度,完成轮廓的匹配工作。
进一步,实验猪舍长度为4m,宽为3.5m,围栏高1m,猪舍中安放了体态、颜色、生长期各有差异的7头猪,拍摄俯视视频的摄像机安装在猪舍正上方,距离地面高度约3m,采集到包含背景的俯视状态下群养猪的rgb彩色视频。
进一步,所述步骤2的具体过程为:
将任一曲线看作为一系列点的集合,逐步减少点的数量,从而去掉了其他对曲线影响相对较弱的点,但对于一些复杂曲线,阈值t选取过大时容易出现自相交现象,阈值t选取过小时达不到多边形近似的效果,通过反复试错选取经验值;
获取曲率最大的点:在数字图像中,轮廓是一系列离散坐标点的集合,曲率可以通过插值的方法来近似定义,假设曲线方程为y=y(x),曲率定义为:
根据不共线3点确定一个圆的公理,多边形上任意相邻的3个顶点(pi-1,pi,pi+1)可以构成圆的一段弧,线段pi+1pi和pipi-1中垂线的交点o就是圆的圆心,过点pi且垂直于opi的直线m即为点pi的切线,pi的一阶导数就是直线m的斜率,记作ki,同理可获取pi+1和pi-1的一阶导数;然后采用三次hermite差值定义[pi,pi+1]的近似曲线:
si(x)=h0(x)pi+h1(x)pi+1+h2(x)ki+h3(x)ki+1(7)
式(7)中,hi(x)|i=0,1,2,3是混合函数,对方程求二阶导得到:
si”(0)=-6pi+6pi+1-4ki-2ki+1(8)
综合式(6)和(8)得到点pi处的曲率:
进一步,所述步骤(3)的具体过程为:
假设轮廓上有个k个保留点,分别是p1,p2,…,pk,用
为了保持尺度不变性,在选取距离作为特征时不能选取绝对距离,而应该选取相对距离,同时又为了反映轮廓各点的分布情况,定义基向量
按照向量的夹角公式可知,
角度特征具有天然的尺度不变性和旋转不变性,但当轮廓的起始点选取不同时,夹角θ可能会是锐角或者钝角,但锐角加上钝角的和为180°,这里统一采用锐角做为特征角度,因此定义基向量
因此,基向量
p={p1,p2,...,pk-1}(14)
进一步,所述步骤(4)的具体过程为:
给定两个轮廓s1和s2,它们的轮廓特征描述子分别是p={p1,p2,...,pn1}和q={q1,q2,...,qn2},假定p和q的对应关系用集合f表示,f的元素是一个分配(i,j),其中pi∈p,qj∈q,求解p和q的正确匹配即求解f的一个子集f,使得满足子集f中所有分配的匹配最优;设相似度为h(s1,s2),要计算其值首先需找到p和q之间基向量的映射关系,这里根据轮廓基线段的个数,映射关系最多有
对于每一个最优分配a=(i,j),这里采用x2距离统计分布来度量pi和qj的匹配代价,公式如下:
该代价值介于0到1之间,其值越小,pi和qj的相似程度越大,对于轮廓所有基向量的代价值cij的集合,可以得到总的代价值,其值越小,说明两个轮廓越相似;这样求解轮廓的相似度就转为求解最优匹配f,利用匈牙利算法可以得到代价最小的最优匹配,得到轮廓基向量之间的最优匹配关系,当最优匹配下的基向量之间的代价值小于某个阈值t时,就认为该基向量匹配正确,最后计算待匹配轮廓上正确匹配的基向量个数和训练样本轮廓上基向量的总数的比值,从而得到两个轮廓之间的相似度,完成轮廓的匹配工作。
本发明的有益效果是:
传统人工观察识别猪只饮水行为的方式费时费力,且影响工作人员的健康。耳标rfid方式虽然无需人工实时观察,但是它是一种侵扰式方法,也会一定程度上干扰猪只正常生活和生长。通过机器视觉技术无应激对猪只饮水行为进行识别,有助于实现自动监控猪舍内猪只的饮水行为,并及时预警异常猪只,同时减少猪只饲养过程中的人工干扰活动,改善猪只福利,对提高规模养殖业自动化和智能化监控水平提供技术支撑。
附图说明
下面结合附图和具体实施方式对本发明做进一步详细说明:
图1是猪只饮水行为识别流程图。
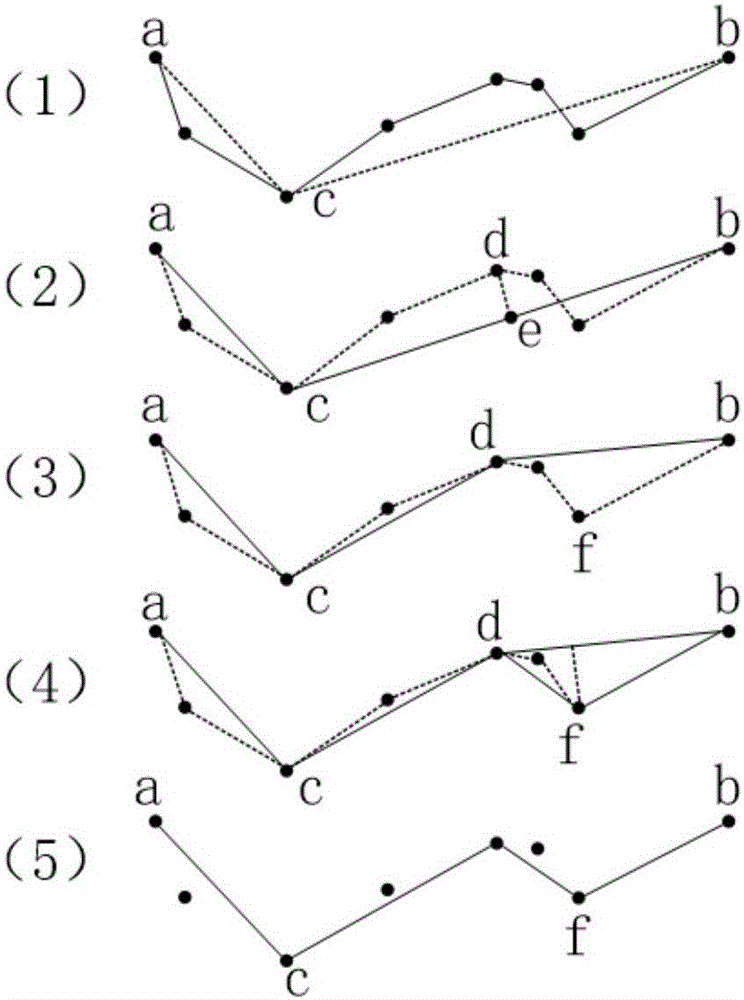
图2是轮廓的多边形拟合示例图。
图3是离散点曲率定义示例图。
图4是轮廓特征提取示例图。
具体实施方式
下面结合该图,进一步说明具体涉及的各部分具体实施方式。
图1为猪只饮水行为识别流程图,饮水区域提取和轮廓提取的目的是获取该区域内猪只轮廓;轮廓多边形近似法完成轮廓的多边形拟合;轮廓特征提取采用角度和距离来构建二维特征量;相似度计算采用匈牙利算法进行最优匹配,并通过计算两个多边形之间的相似度,完成待识别轮廓和训练样本轮廓的匹配;最终可以实现基于机器视觉的猪只饮水行为识别方法。
步骤1:获取俯视状态下群养猪视频,然后进行图像预处理,主要是饮水区域内猪个体目标的提取,最后是样本库的建立。
(1)获取俯视状态下群养猪视频。
实验猪舍长度为4m,宽为3.5m,围栏高1m,猪舍中安放了体态、颜色、生长期各有差异的7头猪,拍摄俯视视频的摄像机安装在猪舍正上方,距离地面高度约3m,可以采集到包含背景的俯视状态下群养猪的rgb彩色视频。
(2)对单帧图像采用改进的二维otsu图像算法进行分割。
选取符合条件的视频帧,对单帧图像采用改进的二维otsu图像算法进行分割,具体过程如下:首先设原始二维灰度直方图为ω,将纵轴和横轴分成m组,每组有n(l/m)个灰度级,其中l为图像灰度级,这样ω分为m×m个区域,即
ω={ωpq|p,q=0,1,…,m-1}(1)
其中p,q分别是纵横轴的组号,每个区域有n×n个点,即区域:
ωpq={(pn,qn),(pn+1,qn),…((p+1)n-1),(qn+1),…,((p+1)n-1)(q+1)n}(2)
其中(pn,qn)表示ω中横坐标pn纵坐标qn的点。
ωpq内的概率之和
将每个区域ωpq合并成一个点,建立一个新的二维直方图ω',对ω'使用二维otsu算法,得到阈值(s,t):
由(s,t)可知道分割阈值的位置,即位于区域ωst内。对ωst使用二维otsu算法:
最后得到原图像的分割阈值(s',t'),从而实现目标的分割。
步骤2:将任一曲线看作为一系列点的集合,逐步减少点的数量,达到简化曲线的目的;经过多次化简,保留其中满足条件的坐标点,从而去掉了其他对曲线影响相对较弱的点,对猪个体的轮廓进行多边形拟合。
图2的算法具体描述如下:
(1)计算各点的曲率,取曲率最大的点c,连接首尾两点和点c,得到两条线段ac和cb,然后分别进行处理;
(2)对于线段cb,计算这两点之间其他点到该线段的距离,取线段de为最大距离dmax,对应的轮廓点为点d;
(3)比较dmax和给定阈值t的大小关系:如果dmax小于t,该直线段cb作为曲线的近似,如果dmax大于t,则曲线被分割为cd和db两段;
(4)重复上述2步的操作,直到c点到b点之间的轮廓全部处理完毕;
(5)对于线段ac,采取上述3步的操作,最后得到完整的近似曲线。
算法原理示意如图2所示。在图2(1)中a和b之间共有坐标点6个,经过3次化简,保留其中满足条件的3个坐标点,从而去掉了其他对曲线影响相对较弱的点,算法简单、高效、直观形象。对于如图2中的简单曲线,其形态特点得到了完整的保留,但对于一些复杂曲线,阈值t选取过大时容易出现自相交现象,阈值t选取过小时达不到多边形近似的效果,因此这里选取经验值t=0.3。
在轮廓多边形近似算法第一步中,需获取曲率最大的点。在数字图像中,轮廓是一系列离散坐标点的集合,曲率可以通过插值的方法来近似定义。假设曲线方程为y=y(x),曲率定义为:
根据不共线3点确定一个圆的公理,多边形上任意相邻的3个顶点(pi-1,pi,pi+1)可以构成圆的一段弧,线段pi+1pi和pipi-1中垂线的交点o就是圆的圆心,过点pi且垂直于opi的直线m即为点pi的切线,如图3所示,pi的一阶导数就是直线m的斜率,记作ki,同理可获取pi+1和pi-1的一阶导数。然后采用三次hermite差值定义[pi,pi+1]的近似曲线:
si(x)=h0(x)pi+h1(x)pi+1+h2(x)ki+h3(x)ki+1(7)
式(7)中,hi(x)|i=0,1,2,3是混合函数,对方程求二阶导得到:
si”(0)=-6pi+6pi+1-4ki-2ki+1(8)
综合式(6)和(8)得到点pi处的曲率:
曲率体现了曲线的弯曲程度,值越大表明该处曲线的弯曲程度越大。对于饮水猪只头部而言,曲率的极值点也正是多边形近似时需要保留的点。
步骤3:轮廓特征提取,针对近似得到的多边形,提取具有代表性的多边形特征。
假设轮廓上有个k个保留点,分别是p1,p2,…,pk,用
为了保持尺度不变性,在选取距离作为特征时不能选取绝对距离,而应该选取相对距离,同时又为了反映轮廓各点的分布情况,定义基向量
按照向量的夹角公式可知,
角度特征具有天然的尺度不变性和旋转不变性,但当轮廓的起始点选取不同时,夹角θ可能会是锐角或者钝角,但锐角加上钝角的和为180°,这里统一采用锐角做为特征角度,因此定义基向量
因此,基向量
p={p1,p2,...,pk-1}(14)
步骤4:相似度计算,通过计算轮廓特征量构成的矩阵之间的相似度识别猪只的饮水状态。
给定两个轮廓s1和s2,它们的轮廓特征描述子分别是p={p1,p2,...,pn1}和q={q1,q2,...,qn2},假定p和q的对应关系用集合f表示,f的元素是一个分配(i,j),其中pi∈p,qj∈q,求解p和q的正确匹配即求解f的一个子集f,使得满足子集f中所有分配的匹配最优。这里主要研究的是轮廓的匹配,因此允许p中某个基向量最多只能和q中一个基向量达成匹配,计算轮廓间的相似度的问题就转换成了计算最优解的问题。
设相似度为h(s1,s2),要计算其值首先需找到p和q之间基向量的映射关系,这里根据轮廓基线段的个数,映射关系最多有
对于每一个最优分配a=(i,j),这里采用x2距离统计分布来度量pi和qj的匹配代价,公式如下:
该代价值介于0到1之间,其值越小,pi和qj的相似程度越大,对于轮廓所有基向量的代价值cij的集合,可以得到总的代价值,其值越小,说明两个轮廓越相似。这样求解轮廓的相似度就转为求解最优匹配f,这是一个最优化问题求解,同时也是一个典型的线性分配问题。在实际应用中,通常采用匈牙利算法进行求解。利用匈牙利算法可以得到代价最小的最优匹配,得到轮廓基向量之间的最优匹配关系,当最优匹配下的基向量之间的代价值小于某个阈值t时,就认为该基向量匹配正确,最后计算待匹配轮廓上正确匹配的基向量个数和训练样本轮廓上基向量的总数的比值,从而得到两个轮廓之间的相似度,完成轮廓的匹配工作。经上述步骤,可以实现对待识猪只饮水状态的识别。
综上,本发明的一种利用机器视觉技术对俯视群养猪视频中猪只饮水行为进行识别的方法。首先从采集的俯频视群养猪视帧分离出饮水区域,并采用二维otsu法得到初步分割结果,对该结果进行二值化以及形态学处理,获得目标轮廓;其后采用多边形近似法得到轮廓的多边形拟合图,针对该多边形,提取具有尺度不变性和旋转不变性的二维特征量;接着通过匈牙利算法对两个多边形相关特征量进行最优匹配;最后计算两个多边形之间的相似度,完成待识别轮廓和训练样本轮廓的匹配,实现猪只的饮水行为识别。该方法为今后对群养猪采食、排便等行为的识别研究打下了基础,也为探索畜牧的行为识别方法提供了新思路。
在本说明书的描述中,参考术语“一个实施例”、“一些实施例”、“示意性实施例”、“示例”、“具体示例”、或“一些示例”等的描述意指结合该实施例或示例描述的具体特征、结构、材料或者特点包含于本发明的至少一个实施例或示例中。在本说明书中,对上述术语的示意性表述不一定指的是相同的实施例或示例。而且,描述的具体特征、结构、材料或者特点可以在任何的一个或多个实施例或示例中以合适的方式结合。
尽管已经示出和描述了本发明的实施例,本领域的普通技术人员可以理解:在不脱离本发明的原理和宗旨的情况下可以对这些实施例进行多种变化、修改、替换和变型,本发明的范围由权利要求及其等同物限定。
- 还没有人留言评论。精彩留言会获得点赞!