基于张量的MPCA动态手势识别方法与流程

本发明涉及计算机视觉、图像处理、模式识别技术领域，特别涉及一种基于张量的mpca动态手势识别方法。

背景技术：

目前，动态手势的数据降维一般采用pca算法，例如，李志强等人在基于kinect数据主成分分析的人体动作识别中运用pca算法对时间帧序列数据降维，而舍弃了对动作分类再结合k近邻算法对人体动作进行识别。经典的pca算法属于线性方法，一般将数据表示为一维向量，通过计算降维后数据总离散度的最大值来寻找最佳降维子空间，常用于简单结构数据的特征提取。

然而，pca为线性降维方法，特征提取时难以利用到数据中的非线性信息，特征表达能力存在局限性，同时它只能反映数据的二阶统计特性，缺乏表征数据高阶统计特性的能力，无法充分利用数据的多阶信息以及数据内部隐含的数据结构信息。

技术实现要素：

本发明的目的是针对现有技术的不足，提出一种基于张量的mpca动态手势识别方法，mpca是指多线性主成分分析算法(multilinearprincipalcomponentanalysis)，以解决原始数据空间维度过大、数据严重冗余等问题，在特征变量提取的过程中保留原始数据的大部分特征信息，有效分析处理高维数据。

为实现上述目的，本发明所设计的基于张量的mpca动态手势识别方法，其特殊之处在于，所述方法包括如下步骤：

1)采集人体手势姿态数据集，并进行张量化处理，形成张量数据集；

2)将所述张量数据集中的样本数据分为手势训练集和手势测试集；

3)通过mpca算法对所述手势训练集中的样本数据进行降维，得到投影矩阵和判别矩阵，并通过所述判别矩阵计算手势训练集中样本数据的张量特征；

4)通过所述投影矩阵计算手势测试集中样本数据的张量特征；

5)采用最近邻算法作为分类器，将所述手势训练集中样本数据的张量特征与手势测试集中样本数据的张量特征逐一匹配，统计匹配结果与张量特征的异同，得到手势识别结果。

优选地，所述步骤3)的具体步骤包括：预处理、初始化投影、局部优化、生成特征子空间、输出投影矩阵和判别矩阵。

优选地，所述预处理的过程为对样本数据进行中心化的过程，所述手势训练集为{χ1,χ2,…,χm}，样本数据为其中为线性空间，in为张量n-模的维度，1≤n≤n，n为张量的阶数，m为样本数，1≤m≤m，预处理后的手势训练集为其中为样本均值。

优选地，所述初始化投影的步骤为：对初始协方差矩阵进行特征分解，其中为中心化后的样本的n-模展开，表示的转置矩阵，将初始协方差矩阵的特征值从大到小进行排列，取其前pn个特征值对应的正交特征向量构建n-模向量空间中的投影矩阵pn为n-模向量空间最终降维的数目。

优选地，所述局部优化的步骤包括：

a)将循环计数k设为0，并设置匹配阈值η和循环次数k；

b)依次计算n-模的协方差矩阵φ⁽ⁿ⁾和投影矩阵1≤n≤n；

c)计算投影后的样本数据

d)计算投影后的样本张量的总离散度

e)判断是否满足或者k＝k，是则前往步骤f)。否则，令k＝k+1，返回步骤b)；

f)输出投影矩阵和判别矩阵ym

优选地，所述n-模向量空间最终降维的数目pn通过计算特征向量的贡献率oval确定，oval≥95％。

优选地，所述步骤4)中计算张量特征的公式为；

优选地，所述循环次数k的值为4。

优选地，所述贡献率oval的取值为98％。

本发明提出的基于张量的mpca算法的手势识别结果优于传统的pca算法以及kmean+pca算法。与现有kmean+pca算法对比，mpca算法在提取较多特征的基础上保留了较高的识别精度。与传统的pca算法对比，基于张量的mpca算法提取较少的特征就能获得较高的识别精度。在这三种方法中，pca算法和kmean+pca算法都采用一维向量的形式表征动态手势，mpca算法运用三阶张量的方式对手势数据建模，并采用子空间投影方法提取手势特征，本发明方法保留了动态手势的结构特征，因此能够有效分析处理高维数据，获得较高的识别率。

附图说明

图1为本发明基于张量的mpca动态手势识别方法的流程图。

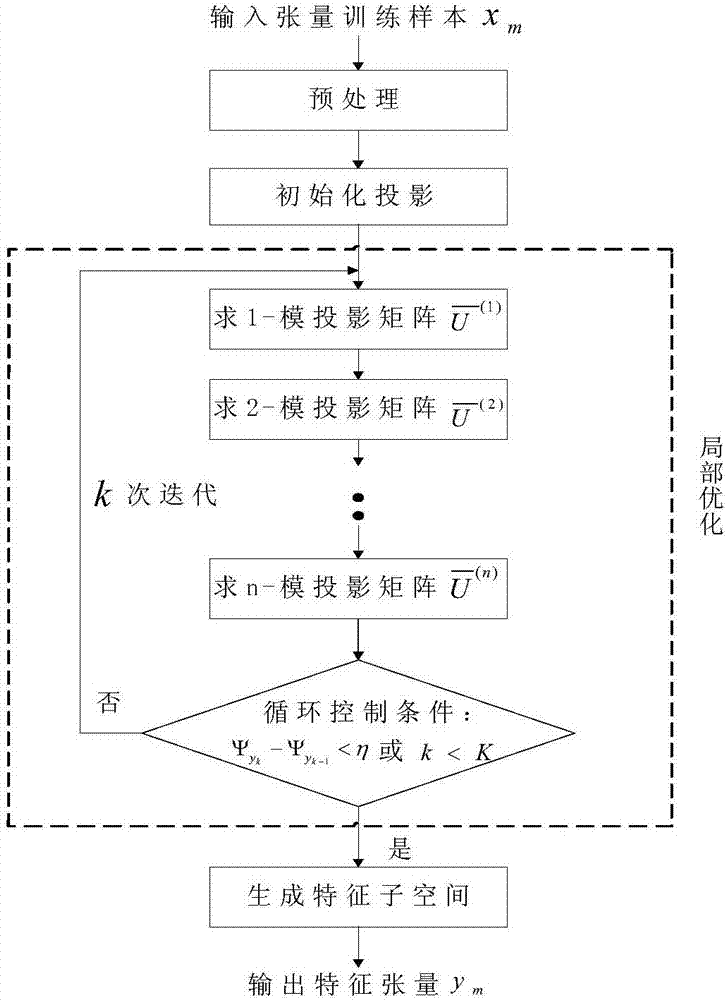
图2为运用mpca算法进行多线性空间降维的流程图。

图3为降维后样本总离散度随迭代次数变化图。

图4为mpca算法手势识别率随qval值变化图。

图5为pca算法手势识别率随特征个数变化图。

图6为手势识别率随l值变化图。

具体实施方式

以下结合附图和具体实施例对本发明作进一步的详细描述。

如图1所示，本发明所设计的基于张量的mpca动态手势识别方法包括如下步骤：

1)采集人体手势姿态数据集，并进行张量化处理，形成张量数据集。

11)数据收集：在数据收集中，通过骨骼数据流、骨骼框架、骨骼模型和关节点这四个对象可以实现人体骨骼追踪功能，通过识别人体20个关键关节点位置来确定人体的三维骨骼模型，从而实现目标人体的三维空间表示。

12)数据预处理：对收集到的人体姿态数据集里的手势序列进行样本抽取，将抽取得到的手势样本表示成三阶张量的形式，其中1-模表示每帧手势的关节点数，2-模表示关节点的三维特征，3-模表示手势序列的帧数，那么每个手势样本都表示成了维度统一的三阶张量样本。其中，手势张量1-模表示每帧手势的关节点数，2-模表示关节点的三维特征，原始手势样本中包含了人体20个关节点的x、y、z三维坐标值，因此手势张量样本的1-模维度和2-模维度分别确定为20和3。3-模维度根据实际得到的样本数据，采用“截头去尾”的方式，将截去手势序列样本中的开始若干帧和结尾若干帧，将所有手势序列样本处理为相同的帧数，根据不同情况自行选取。

2)将张量数据集中的样本数据分为手势训练集和手势测试集。

3)通过mpca算法对手势训练集中的样本数据进行降维，得到投影矩阵和判别矩阵，并通过判别矩阵计算手势训练集中样本数据的张量特征。

4)通过投影矩阵计算手势测试集中样本数据的张量特征。

5)采用最近邻算法作为分类器，将手势训练集中样本数据的张量特征与手势测试集中样本数据的张量特征逐一匹配，统计匹配结果与张量特征的异同，得到手势识别结果。

mpca算法的核心是对张量样本在每个模式方向上进行降维，寻找每个模式下的投影矩阵从而构建最佳的多线性子空间，然后在多线性子空间上对张量样本进行降维，从而得到每个模式方向上的主要成分。它允许映射矩阵捕捉原始张量上的大多数变化，包括结构信息和相关性。

假设{χ1,χ2,…,χm}为的手势训练集，其中in是张量n-模的维度(1≤n≤n)，m为样本数。由线性变换的性质可知，运用线性空间中的pn(<in)个正交基向量和相应的投影矩阵就可以将空间映射到子空间上。同理，在n阶张量的每一模上选取线性空间中的pn(<in)个正交基向量(沿主轴方向)，然后选择每模上的投影矩阵，就可以将n阶张量空间映射到子空间上。记矩阵为张量n-模方向上的投影矩阵，则是拥有pn个n-模正交基向量的in×pn矩阵，设张量χm经多元线性变换后为ym，则有

这样m＝1,2,…,m}就能对原始数据进行特征提取，从而达到高阶数据降维的目的。

由于张量样本的总离散度ψy是衡量张量变化的物理量，因此mpca算法的目标函数是确定n个投影矩阵使得线性变换后的样本{y1,y2,…ym,…,ym}的总离散度ψy最大化，即满足

这样，通过寻找多元线性变换即n个投影矩阵就可以捕捉到原始张量样本中的绝大多数变化。在确定投影矩阵前，张量子空间的维度pn假定为已知或预先已确定。若张量的每模子空间维度pn不能事先确定，可以运用自适应算法来确定pn的值。

mpca算法的目标是同时找到n个投影矩阵使得总离散度ψy最大化，但是目前没有最佳的优化解决方案。然而n阶张量的子空间映射难题可以转化为张量空间到n维向量子空间的n个映射优化子问题，若寻找到n-模向量空间中的投影矩阵使得协方差矩阵φ⁽ⁿ⁾最大化，那么n个映射优化子问题就可以得到解决。

假定是式(2)的解，若其他的投影矩阵已给定，那么n-模向量空间中的协方差矩阵φ⁽ⁿ⁾可以由下面两个式子和给定的n-1个投影矩阵定义：

其中表示kronecker积，χm(n)为训练样本集{χ1,χ2,…,χm}中样本χm的n-模展开矩阵，为n-模均值张量，τ表示转置符，n＝1,…,n。协方差矩阵φ⁽ⁿ⁾的pn个最大特征值对应的pn个特征向量就构成了投影矩阵由式(3)和式(4)可知，的乘积由决定，因此矩阵的优化问题依赖于其他模态下的投影矩阵对于这种互相依赖的优化子问题，目前没有比较直接的解决方案，但可以通过迭代法间接解决这个难题。

步骤3)是本发明最重要的部分，如图2所示，运用mpca算法进行多线性空间降维的具体步骤包括：预处理、初始化投影、局部优化、生成特征子空间、输出投影矩阵和判别矩阵。

31)：预处理。

{χ1,χ2,…,χm}为的手势训练集，其中in是张量n-模的维度(1≤n≤n)，m为样本数，n为张量的阶数。对输入样本进行中心化，中心化后的样本集为其中为样本均值。

32)：初始化。

对初始协方差矩阵进行特征分解，其中为中心化后的样本的n-模展开，表示的转置矩阵，将初始协方差矩阵的特征值从大到小进行排列，取其前pn个特征值对应的正交特征向量来构建n-模向量空间中的投影矩阵pn为n-模向量空间最终降维的数目，一般需要通过计算特征向量的贡献率oval来确定，oval取大于95％的值，其中n＝1,…,n。

33)：局部优化。

a)将循环计数k设为0，并设置匹配阈值η和循环次数k；

b)令n＝1,…n，根据式

求协方差矩阵φ⁽ⁿ⁾，取其前pn个最大特征值对应的正交特征向量来构建投影矩阵其中n＝1,…n。

c)计算投影后样本数据

d)计算投影后的样本张量的总离散度因为是中心化后的样本数据，投影后样本的均值张量的值为零，所以简化为

e)判断循环是否结束，如果或者k＝k，则停止循环，跳到步骤f)，否则，令k＝k+1，将得到的投影后的样本数据作为新的样本数据输入，返回b)；

f)输出投影矩阵和判别矩阵ym

34)：映射。

循环迭代结束即可得到投影矩阵那么手势训练集中样本数据的张量特征可以通过判别矩阵计算获得。输入张量样本在子空间中的低维表示为

实施例

抽取微软人体姿态数据集的9类手势，共包括89个序列，每个手势序列都包含一个.csv文件和相应的.tagstream文件，并且.csv文件中包含每帧深度图的关节点信息和时间戳，.tagstream文件记录了相应序列中手势表演重复的起始时刻以及重复次数。

在所有手势序列中，手势均被重复表演多次，因此每个序列都可以被分成若干个手势样本。通过对比.tagstream文件中记录的手势重复表演起始时刻和.csv文件中的时间戳，可以将手势序列分成若干个手势样本。

本发明研究的9类手势共有89个序列，这些序列分解出的手势样本共913个，每类手势的序列总数和划分序列得到的手势样本总数如表1所示。

表19类手势及其序列总数、样本总数

根据手势张量化表示方法，可以确定手势张量1-模和2-模的维度。手势张量1-模表示每帧手势的关节点数，2-模表示关节点的三维特征，原始手势样本中包含了人体20个关节点的x、y、z三维坐标值，因此手势张量样本的1-模维度和2-模维度分别确定为20和3。

研究每类手势序列的帧数变化规律和表征手势主要变化的若干帧3d图有助于确定手势张量的3-模维度(序列或时间维度)。通过3d效果图可以直观且清晰的看到每类样本序列中手势的变化。采用“截头去尾”法截去手势序列样本中的开始若干帧和结尾若干帧，将所有手势序列样本处理为60帧。

利用这种张量化表示方法，每个手势序列样本都可以表示成一个20×3×60的三阶手势张量。也就是说，本文用作实验的手势序列样本集可以表示为如下的张量集：

其中，表示第j类手势中的第i个样本，mj表示第j类手势的样本总数，即mj为向量m＝(92,103,101,103,101,101,101,105,106)中的第j个值。这样，就完成了mpca算法的输入张量集—手势张量集的构建。

从手势张量集和手势向量集中随机抽取一定比例的样本构造训练集，剩余的样本则组成测试集。抽取比例设为50％，则测试集样本总数为406，每类手势的训练样本数和测试样本数如表2所示：

表2每类手势的训练样本数和测试样本数

运用mpca算法提取手势特征时，循环迭代次数k的值决定了投影矩阵的优化程度，参数qval的值决定了每模投影矩阵的维度。也就是说，循环迭代次数k和参数qval的值均会影响最终的手势识别结果。因此，在实验数据上测试mpca算法的特征提取效果前，必须先确定参数k和参数qval的大小。在采用matlab编写的mpca.m文件中，变量qval表示特征提取时保留原始信息的百分比。在mpca算法中，确定每模投影矩阵维度时，设定每模的参数变量qval为相同的百分数，若设为97％，那么通过投影矩阵映射得到的每模特征都将保留该模原始数据97％的特征信息。

首先确定循环迭代次数k。将mpca算法中的参数变量qval的值设定为97％，那么手势张量每模投影矩阵的维度就确定了。迭代次数k依次取1到10之间的10个数，研究降维后样本总离散度ψy随迭代次数的变化规律。训练样本集降维后总离散度ψy随迭代次数的变化规律如图3所示。

由图3可以看出，采用mpca算法提取手势特征时，随着循环迭代次数的增加，样本降维后的总离散度会增加；当迭代次数增加到某个值时，样本降维后的总离散度达到最大，并且随着迭代次数的增加，总离散度不再增大且趋于稳定。可以结合mpca算法的迭代求解步骤解释该结果。当迭代次数越多时，投影矩阵的优化程度越高，张量样本经投影矩阵降维后的总离散度越大。当总离散度达到最大值后，投影矩阵即为最优，因此随着迭代次数的增加，投影矩阵将不再优化，样本降维后的总离散度也不再增大且趋于稳定。由图3可知，当迭代次数为4时，样本降维后的总离散度达到最大，此时投影矩阵达到最优。因此采用mpca算法降维时，训练样本的迭代次数设定为k＝4。

确定迭代参数k的值后需要确定mpca算法中的另一个参数qval的值。参数变量qval的值决定了张量样本每模投影矩阵的维度。为研究mpca降维算法中参数变量qval取不同值时手势识别率的变化情况，qval取95％到99％之间的9个数据，循环迭代次数设置为k＝4，在测试样本集上进行实验仿真，得到如图4所示的手势识别结果。由图4可知，qval的值为98％时，手势识别率达到最高且为85.98％。

作为对比，采用pca算法对手势降维，改变降维后的手势特征个数，从而研究手势识别率随特征个数的变化情况。手势特征的维度依次取30到120之间的数，在手势向量测试样本集上进行仿真，得到图5中的手势识别结果。

参照李志强等人在基于kinect数据主成分分析的人体动作识别提出的方法，可以得出基于kinect数据的动态手势的识别步骤：首先参照韩旭的应用kinect的人体行为识别方法研究与系统设计提取手势描述特征向量，用人体结构向量间的20组夹角和4组模比值表示每帧手势；然后采用kmean聚类方法获得每类手势的l个子类，并将每个子类的类心作为模板数据；接着利用所有子类的模板数据构造矩阵，并采用pca算法对该矩阵降维，得到降维后特征矩阵；最后通过k近邻算法计算手势的成功识别率。

按照上述步骤，在实验数据上进行仿真，研究该方法的手势识别效果。根据上述方法，动态手势的每一帧可表示成维度为24的特征向量，那么，包含60帧数据的动态手势序列可以用维度为1440的高维向量表示。也就是说，动态手势的原始特征维度为1440。采用pca算法对原始特征降维时，参数testq决定了降维的维度，参照设定该值为95％。李志强等人在基于kinect数据主成分分析的人体动作识别中未给出kmean聚类算法中子类数l的参考值，本实施例手势样本类别数为9，因此子类数l依次取1～9，研究不同l值对手势识别效果的影响。由于聚类开始点的选取对kmean聚类结果有所影响，因此对每类手势聚类时，重复20次实验，取20次实验的平均值作为每个子类的类心，然后采用pca算法对其降维，最后运用近邻算法对手势分类。表3给出了该方法在不同l值下的手势识别结果。

表3手势识别结果随l值变化规律

由表3可知，当子类数l＝4时，手势识别效果最佳且识别率为76.05％。此时每类手势聚类数为4，且降维后特征数为15。也就是说一个原始特征维度为1440的动态手势只需要提取15个特征就能表示其绝大部分变化。图6给出了手势识别率随子类数l的变化情况。由该图可以看出，手势识别率随子类数的增加呈现先增后减的趋势。在李志强等人提出的方法中，同一类手势的l个子类被当做不同的类来处理。当聚类的子类数过少时，近邻算法对不同人的同一类手势不够敏感，因此手势识别效果不佳；当聚类的子类数过多时，容易将相似度高的不同手势误判，因此手势识别率会降低。所以，采用这种方法识别动态手势时，选择合适的聚类数对于手势识别结果至关重要。

由图4和图5可知，采用mpca算法提取手势张量特征时，当迭代次数k＝4，参数qval＝98％，测试样本集的手势识别效果最好且识别率达85.98％。此时手势张量样本的维度由20×3×60降为4×3×4。也就是说，mpca算法取得最佳识别率时，提取的特征个数为48。由图6可以看出，采用pca算法对手势向量降维的过程中，当降维特征数为90时，手势识别成功率最高且为79.38％。根据表3可知，采用kmean+pca算法提取手势特征时，特征个数为15时，手势识别率最高且为76.05％。表4对比了mpca算法、pca算法和kmean+pca算法的手势识别结果。

表4mpca算法和pca算法识别结果对比

本说明书中未作详细描述的内容属于本领域专业技术人员公知的现有技术。