基于Lu模型的大坝下游河岸带热流耦合模拟构建方法与流程

本发明属于水利工程技术领域，涉及一种基于lu模型的大坝下游河岸带热流耦合模拟构建方法。

背景技术：

在河流上筑坝建库，是开发利用水资源中最常见的工程措施。然而，水库建成蓄水后，形成了庞大的水域，改变了原天然河流的水域环境，形成了特有的温度场。水库发电为主的引水主要取自水温偏低的滞温层，以利用发电尾水进行农业灌溉、生态补水、水厂取水等为主的生产生活性用水水温，在每年绝大多数月份中比河道自然水温低。低温水泄入下游河道，沿程流动并通过侧向潜流交换作用，改变了河岸带潜流层天然温度场和水分场的分布，从而对依存其中的动物群落、作物生长、土壤呼吸等生存环境产生较大的影响，这对河流的可持续健康发展十分不利。

虽然国内外学者基于水库水温或下游河道水温模型进行了大量的研究，同时也有学者利用饱和多孔介质水热耦合运移数学模型分析了水库下泄低温水水位和水温对地表水-地下水交错带温度场的影响规律，已取得了一些研究成果，但目前尚缺少水库下泄低温水造成的河岸带饱和-非饱和热流耦合特性及模型方面的研究成果。

技术实现要素：

本发明的目的是提供一种基于lu模型的大坝下游河岸带热-流耦合模拟构建方法，解决了现有技术中存在的不能够准确的模拟大坝下泄低温水对河岸带饱和-非饱和热-流耦合的影响机理的问题。

本发明所采用的技术方案是，基于lu模型的大坝下游河岸带热流耦合模拟构建方法，包括以下步骤：

步骤1，构建河岸带饱和-非饱和渗流场-温度场全耦合模型，包括建立渗流场，并建立饱和-非饱和热量运移模型，描述温度场和渗流场的关系；

步骤2，对河岸带饱和-非饱和渗流场-温度场全耦合模型设置边界条件，包括对渗流场设置边界条件以及对温度场设置边界条件；

步骤3，求解河岸带饱和-非饱和渗流场-温度场全耦合模型，求解的过程中采用lu模型来描述土体的等效热传导系数与含水率之间的关系，从而得到渗流过程中温度随时间的变化规律。

步骤1中，建立的渗流场具体为河岸带饱和-非饱和瞬态渗流场，采用richards方程进行描述：

式中：θ为含水量，k为土渗透系数，k在饱和区域为初始温度场t的函数，k在非饱和区域为土体基质吸力或含水率的函数；h为压力水头，h为总水头，c为土体容水度，n为多孔介质的孔隙率，ss为弹性贮水率，qs为渗流源汇项，为拉普拉斯方程，dt为水动力弥散系数，t为时间。

在河岸带饱和-非饱和瞬态渗流场中，采用vangenuchten模型来描述非饱和带土壤水分特征曲线：

上式中，h(θ)为土壤基质吸力，k(θ)为非饱和土渗透系数；θs和θr分别为土壤饱和含水率和土壤残余含水率，与土壤质地有关；α和nv为vg模型参数，m＝1-1/nv；ks为饱和土体渗透率。

步骤1中，采用热对流方程描述饱和-非饱和热量运移模型：

式中：c为土体比热容，ρ为土体等效密度，为拉普拉斯方程，λ为土体的等效热传导系数，cw为水的比热容，ρw为水的密度，v为水的平均流速，t为初始温度场，qh为温度场源汇项。

步骤2具体为：

对于渗流场，河岸上下游的边界分别设置为定水头边界，河岸非上下游的边界设置为零通量边界；

对于温度场，河岸水面以下位置设置为定温度边界，河岸底部边界设置为绝热边界，与大气接触的位置取日平均气温值作为边界值。

步骤3的具体步骤为：

步骤3.1，输入参数：土体的等效热传导系数λ、石英含量q、多孔介质的孔隙度n、干土的导热系数λdry、水的导热系数λw、石英的导热系数λq、差值系数ke、其他矿物质的导热系数λ0、土中固体颗粒的导热系数λs、饱和土体的导热系数λsat；

步骤3.2，输入渗流场和温度场的边界条件，并给出水的黏度与温度的关系：μ(t)＝0.00002414×10^{(247.8/(t+133.16)}；

步骤3.3，建立lu模型，将土体的等效热传导系数λ修改为非饱和土的导热系数表达式；

步骤3.4，更新河岸带饱和-非饱和渗流场-温度场全耦合模型的参数分布，即在每个时间步长更新步骤3.1输入参数中的变量，直至河岸带饱和-非饱和渗流场-温度场的求解收敛，得到每个时间步长内的温度值，从而得到渗流过程中温度随时间的变化规律。

步骤3.3中建立lu模型具体为：

通过在干土的导热系数和饱和土的导热系数间插值，得到非饱和土的等效热传导系数λeq：

λeq＝(λsat-λdry)ke+λdry(5)

式中，ke为插值系数，λdry为干土的导热系数，λsat为饱和土的导热系数：

λdry＝-0.56n+0.51(7)

其中：α对于砂土、壤土、粘土分别为1.05、0.9、0.58，sr为饱和度，n表示多孔介质的孔隙度，λw为水的导热系数，λs为土中固体颗粒的导热系数，λs＝λq^qλ0^1-q，其中：q为石英含量，λq为石英的导热系数，λ0为其它矿物的导热系数。

本发明的有益效果是：

(1)基于lu模型的河岸带饱和-非饱和渗流场-温度场全耦合模型模拟的温度与实测值比较吻合，均方根误差(resm)比较小，模型的模拟结果可靠；pearson相关系数(pcc)变化范围在0.51～1.0之间，其中有88.24％的模拟值与实验值呈强相关，剩下的11.76％均处于中等相关，模拟值与实验值相关性比较好；nash-sutcliffe模型效率系数(nse)大于0.6占76.47％，土壤温度的模拟值与实测值之间具有较好的一致性；采用lu模型计算的各项指标均优于未采用lu模型的模拟值；lu模型对土壤导热率具有较好的拟合效果，采用lu模型能够较为精确的刻画河岸带土体在受到大坝下泄低温水时温度的动态变化过程；

(2)离入渗边界和底边界附近的土体在比较短的时间内快速下降并达到稳态，其温度大致接近于入渗水温，相反，靠近上边界和右边界的温度则需要较长的时间达到稳态；离入渗边界越近的区域受到水温的影响越明显，随着入渗水头增加，土壤内部平均温度降低，土壤深层低温区域逐渐扩大，温度梯度增加；

(3)基于lu模型的大坝下游河岸带热流耦合模拟构建方法，阐明了水库低温水入渗条件下外界环境因素变化与和河岸带饱和-非饱和热流动态特征的内在联系，揭示水库下泄低温水对河岸带饱和-非饱和热流耦合的影响机理，对研究地下动植物受低温水影响的生存环境条件所可能采取的工程或非工程措施，具有重要的学术价值和实际应用意义。

附图说明

图1是求解河岸带饱和-非饱和渗流场-温度场全耦合模型的流程图；

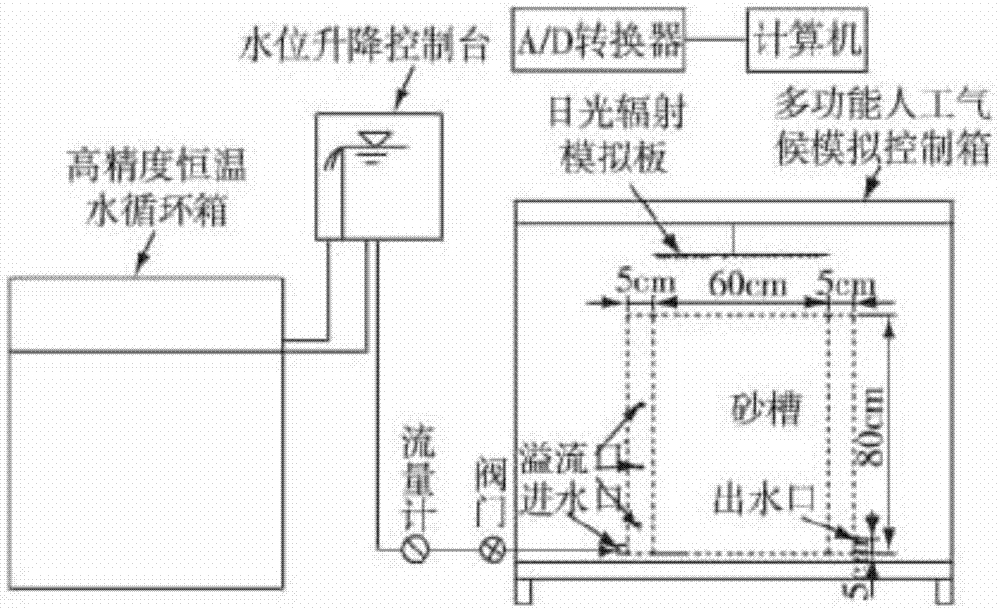
图2室内试验采用的装置的示意图；

图3是室内试验中温度传感器布置示意图；

图4是低温水入渗土壤水热模拟求解区域的示意图；

图5是基于lu模型和无lu模型的模拟与实测在距离入渗边界不同位置纵剖面各点处温度随时间的变化曲线图。

具体实施方式

下面结合附图和具体实施方式对本发明进行详细说明。

取实际工程的河岸带土料的热特性参数，如表1所示，运用基于lu模型的大坝下游河岸带热流耦合模拟构建方法进行热流耦合特性模拟，以保证数值模拟的结果能够对实际工程具指导意义。

表1实际工程的河岸带土料的热特性参数

其中，vg模型参数l属于软件默认值；

基于lu模型的大坝下游河岸带热流耦合模拟构建方法，其特征在于，包括以下步骤：

步骤1，构建河岸带饱和-非饱和渗流场-温度场全耦合模型，包括建立渗流场，并建立饱和-非饱和热量运移模型，描述温度场和渗流场的关系；

步骤1中，建立的渗流场具体为河岸带饱和-非饱和瞬态渗流场，采用richards方程进行描述：

式中：θ为含水量，k为土渗透系数，k在饱和区域为初始温度场t的函数，k在非饱和区域为土体基质吸力或含水率的函数；h为压力水头，h为总水头，c为土体容水度，n为多孔介质的孔隙率，ss为弹性贮水率，qs为渗流源汇项，为拉普拉斯方程，dt为水动力弥散系数，t为时间；

在河岸带饱和-非饱和瞬态渗流场中，采用vangenuchten模型来描述非饱和带土壤水分特征曲线：

上式中，h(θ)为土壤基质吸力，k(θ)为非饱和土渗透系数；θs和θr分别为土壤饱和含水率和土壤残余含水率，与土壤质地有关；α和nv为vg模型参数，m＝1-1/nv；ks为土体饱和渗透率；

步骤1中，采用热对流方程描述饱和-非饱和热量运移模型：

式中：c为土体比热容，ρ为土体等效密度，为拉普拉斯方程，λ为土体的等效热传导系数，cw为水的比热容，ρw为水的密度，v为水的平均流速，t为初始温度场，qh为温度场源汇项。

步骤2，对河岸带饱和-非饱和渗流场-温度场全耦合模型设置边界条件，包括对渗流场设置边界条件以及对温度场设置边界条件：

对于渗流场，河岸上下游的边界分别设置为定水头边界，河岸非上下游的边界设置为零通量边界；

对于温度场，河岸水面以下位置设置为定温度边界，河岸底部边界设置为绝热边界，与大气接触的位置，其温度具有季节波动，取日平均气温值作为边界值。

步骤3，如图1所示，求解河岸带饱和-非饱和渗流场-温度场全耦合模型，本实施例以comsolmutiphsic软件为基础，修改相关模块，实现温度场与渗流场耦合的数值模拟；采用多孔介质和地下水流动模块中的richards’equation组件和热传递模块下的heattransferinporousmedia组件，设置对流传热方程的流速项为饱和-非饱和渗流模块计算得到的水流流速；由于热传递模块默认的热参数是采用体积平均法，即假设多孔介质的热参数是固液两相物质热参数的体积加权平均，描述多孔介质导热参数与饱和度的关系，这就需要修改相关选项，即求解的过程中采用lu模型来描述土体的等效热传导系数与含水率之间的关系，从而得到渗流过程中温度随时间的变化规律；

步骤3.1，输入参数：土体的等效热传导系数λ、石英含量q、多孔介质的孔隙度n、干土的导热系数λdry、水的导热系数λw、石英的导热系数λq、差值系数ke、其他矿物质的导热系数λ0、土中固体颗粒的导热系数λs、饱和土体的导热系数λsat；

步骤3.2，输入渗流场和温度场的边界条件；并给出水的黏度与温度的关系：μ(t)＝0.00002414×10^{(247.8/(t+133.16)}；

如图2所示，计算区域为一个高(垂直方向)80cm，长(水平方向)60cm的矩形区域，图中od为低温水入渗的土壤左边界，oe为入渗水面，oa、cd和ac分别为土体的下边界、上边界和右边界；假定整个模拟区域内的土壤质地是均一的，且各向同性，对于饱和-非饱和渗流场，上游河岸oe为定水头边界，设置25cm水头；ac边界为自由出流边界；其他边界零通量。对于温度场，oe为定温度边界，底部边界oa为绝热边界；edca边界与大气接触，设置为大气边界，这里设置与室内相同的温度20℃；渗流场的初始条件假设压力水头为0，温度场假设初始温度为土壤初始温度；

步骤3.3，建立lu模型，将土体的等效热传导系数λ修改为非饱和土的导热系数表达式；

土体的等效热传导系数是进行岩土工程中有关传热分析的关键参数，其大小会随土体含水量的空间分布差异而产生变化，温度的变化会影响水体粘度和土体孔隙结构，进而影响导热过程，采用lu模型能有效刻画热传导系数与含水率之间的关系，从而提高计算精度；

建立lu模型具体为：通过在干土的导热系数和饱和土的导热系数间插值，得到非饱和土的等效热传导系数λeq：

λeq＝(λsat-λdry)ke+λdry(5)

式中，ke为插值系数，λdry为干土的导热系数，λsat为饱和土的导热系数：

λdry＝-0.56n+0.51(7)

其中：α对于砂土、壤土、粘土分别为1.05、0.9、0.58，sr为饱和度，常数1.33为形状参数，n表示多孔介质的孔隙度，λw为水的导热系数，λs为土中固体颗粒的导热系数，λs＝λq^qλ0^1-q，其中：q为石英含量，λq为石英的导热系数，λq＝7.7w/(m·℃)，λ0为其它矿物的导热系数，当q>0.2时，λ0＝2.0w/(m·℃)，当q≤0.2时，λ0＝3.0w/(m·℃)；

建立lu模型，修改模块后，河岸带饱和-非饱和渗流场-温度场全耦合模型的参数如表2所示：

表2修改模块后河岸带饱和-非饱和渗流场-温度场全耦合模型的参数表

步骤3.4，更新河岸带饱和-非饱和渗流场-温度场全耦合模型的参数分布，即在每个时间步长更新步骤3.1输入的变量，直至河岸带饱和-非饱和渗流场-温度场的求解收敛，得到每个时间步长内的温度值，从而得到渗流过程中温度随时间的变化规律。

模型验证：

一.进行室内试验：

取实际工程的河岸带土料作为试样，对其进室内河岸带的热-流耦合试验，试验采用有机玻璃制成的二维砂槽，长70cm、宽20cm、高80cm，砂槽左右两端用有机玻璃挡板对称隔成宽5cm的水槽，并在有机玻璃挡板上对称钻有直径5mm左右的透水孔，间距为1cm；上游水槽边壁垂直方向分别设有高25cm的溢流口，保证稳定的上游入渗水头，并在右水槽垂直方向设有高5cm的出水口。砂箱模型的结构如图3所示。试验所用的材料为中细砂土，经风干、去除杂物，过孔径为2mm的筛，混合均匀后，按设定干容重1.56g/cm3分层均匀装入试验砂槽；在填砂土过程中，每填入9cm厚度的砂土就进行压实，并且在砂土层之间进行刨毛。

在土槽前壁均匀埋设了6排共30个温度传感器，从中选取17个温度传感器用于数值模拟分析，17个传感器的位置如图4所示；对于河岸带，环境的因素变化对土壤中的温度场的影响很大，本试验只考虑入渗水温和入渗水头两个影响因素，试验选用入渗水头为25cm，入渗水温为10℃的工况。砂土的初始温度保持在20℃。根据试验方案，在试验开始之前，通过高精度恒温水循环系统制备试验所需的低温水水温，再通过水位升降控制台调节供水强度的大小，并使其稳定。当水温稳定后，同时打开秒表和进水口阀门，进行入渗试验，采样间隔为1分钟，传感器通过采集仪和电脑相连，实时采集，得到温度场数据。

二.进行模型精度评估：

本发明采用均方根误差(rmse)，pearson相关系数(pcc)和nash-sutcliffe模型效率系数(nse)对河岸带饱和-非饱和渗流场-温度场全耦合模型的模拟精度进行评估：

式中：m为实验温度数据的样本容量，tobs,i和tmodel,i分别是第i时刻实验测得的温度与模型模拟值，和分别表示试验和模拟的平均温度。resm的值在0到+∞范围内变化，resm的值越小，表示模拟值与实验值之间的偏差越小，模型的模拟结果越可靠。pcc的值在-1到1范围内变化，pcc的绝对值越大，相关性越强，相关系数越接近于1或-1，相关度越强，相关系数越接近于0，相关度越弱；通常情况下相关系数0.8-1.0极强相关，0.6-0.8表示强相关，0.4-0.6表示中等程度相关。nse的值从-∞到1之间变化可以作为lu模型模拟的标准，当nse接近1.0时，表示实测值和模拟值的完美匹配；当nse>0.6时，认为模拟值和实验值之间一致性比较好；当nse接近0，表明该模型模拟结果等同于实测值的均值系列，即总体结果可信，但过程模拟误差大，而nse远远小于0，则模型是不可信的。

根据室内试验测得的温度场数据和comsolmultiphysics软件模型(分lu模型和无lu模型)得到的温度场数据，图5(a)、5(b)、5(c)、5(d)、5(e)给出了基于lu模型和无lu模型的模拟与实测在距离入渗边界依次为5米、15米、30米、45米、55米位置纵剖面各点处温度随时间的变化曲线，结果的一致性通过表2给出。

表2采用lu和无lu模型的均方根误差(rmse)，pearson相关系数(pcc)和nash-sutcliffe模型效率系数(nse)的模拟结果

从表2可以看出，基于lu模型的resm变化范围在0.14～1.1，平均值为0.51，模拟值与实验值之间偏差比较小。pcc变化范围在0.51～1.0之间，其中88.24％的pcc的值是大于0.8，平均值为0.92，可以看出模拟值与实测值极强相关。nse的值在-4.12～1.0范围变化，平均值为0.31，其中nse>0.6占76.47％，其他的值均在合理范围内，表明模拟值与观测值的一致性比较好。无lu模型的resm变化范围在0.2～1.85，平均值为0.75，pcc变化范围在0.28～1.0之间，平均值为0.86，其中70.59％的pcc的值是大于0.8，nse的值在-5.48～1.0范围变化，平均值为-0.15，其中nse>0.6仅占58.82％，采用lu模型的模拟值各项指标均优于未采用lu模型的模拟值。由此可见，lu模型对土壤导热率具有较好的拟合效果，采用lu导热模型能够较为精确的刻画河岸带土体在受到大坝下泄低温水时温度的动态变化过程。

通过上述方式，本发明基于lu模型的大坝下游河岸带热流耦合模拟构建方法：

(1)基于lu模型的河岸带饱和-非饱和渗流场-温度场全耦合模型模拟的温度与实测值比较吻合，均方根误差(resm)比较小，模型的模拟结果可靠；pearson相关系数(pcc)变化范围在0.51～1.0之间，其中有88.24％的模拟值与实验值呈强相关，剩下的11.76％均处于中等相关，模拟值与实验值相关性比较好；nash-sutcliffe模型效率系数(nse)大于0.6占76.47％，土壤温度的模拟值与实测值之间具有较好的一致性；采用lu模型计算的各项指标均优于未采用lu模型的模拟值；lu模型对土壤导热率具有较好的拟合效果，采用lu模型能够较为精确的刻画河岸带土体在受到大坝下泄低温水时温度的动态变化过程；

(2)离入渗边界和底边界附近的土体在比较短的时间内快速下降并达到稳态，其温度大致接近于入渗水温，相反，靠近上边界和右边界的温度则需要较长的时间达到稳态；离入渗边界越近的区域受到水温的影响越明显，随着入渗水头增加，土壤内部平均温度降低，土壤深层低温区域逐渐扩大，温度梯度增加；

(3)阐明了水库低温水入渗条件下外界环境因素变化与和河岸带饱和-非饱和热流动态特征的内在联系，揭示水库下泄低温水对河岸带饱和-非饱和热流耦合的影响机理，对研究地下动植物受低温水影响的生存环境条件所可能采取的工程或非工程措施，具有重要的学术价值和实际应用意义。