基于数据驱动的近断层非平稳地震动模拟方法与流程

本发明涉及地震动模拟技术领域，特别涉及一种基于数据驱动的近断层非平稳地震动模拟方法。

背景技术：

由地震波传播的地面震动，通常称为地震动，近断层地震动有一些显著区别于中、远场地震动的特点，近断层地震动包含高频成分和低频脉冲成分，由于脉冲成分具有幅值大、持时短的特点，因此会对工程结构造成严重的破坏。然而，近断层地震动实测记录数量非常有限，所以提出针对近断层地震动高效的模拟方法是亟待解决的问题。

目前，国内外学者较常采用反映高频成分的随机模型与简单解析脉冲函数相叠加的模拟方法，其中，利用多种等效脉冲型函数模型进行脉冲速度位移时程的模拟方法，由于等效脉冲模型形状单一，并不适用于具有某些具有特殊形状的实测脉冲记录，而高频成分则需要根据地震动的功率谱模型得到。

另一方面，地震动是一种非平稳随机过程，并且绝大多数地震动记录均反映出强度和频率的双重非平稳性，近断层区域的地震动记录也不例外，平稳地震动的随机模拟是以地震功率谱为基础，通过三角级数叠加法容易获得地震动时程样本，然而与平稳地震动相比，描述地震动非平稳特征的时变功率谱模型没有普遍适用的解析表达式。综上所述，近断层非平稳地震动有效的模拟方法仍存在很大的困难。

目前，非平稳信号分解与重构技术常被用来模拟地震动样本，即利用信号分解方法将原始地震记录转换为多层窄带“子序列”，并在此基础上利用信号重构技术获得近断层地震动的模拟公式。其中，适合于非平稳地震动的分解方法包括离散小波分解、小波包分解、经验模态分解、总体经验模态分解等。经验模态分解、总体经验模态分解方法没有完备的数学基础，很大程度上依赖于使用者的经验；小波分解、小波包分解方法不具有平移不变性，则会引起重构信息的丢失，部分小波系数的扰动还会带来信号的严重失真，与实际信号相差较大，重构模拟结果不够精确。

技术实现要素：

本发明所要解决的技术问题在于针对现有非平稳地震动的模拟方法的不足，提供一种基于数据驱动的近断层非平稳地震动模拟方法，为了实现上述发明目的，本发明提供了以下技术方案：

一种基于数据驱动的近断层非平稳地震动模拟方法，包括如下步骤：

(1)通过swt将原始近断层非平稳地震动记录分解为若干个单分量信号的叠加；

(2)分别对每一阶所述单分量信号利用hilbert变换得到其瞬时幅值与瞬时相位，并根据所述瞬时相位求得瞬时频率；

(3)利用均匀分布的初始相位角以及高斯分布的瞬时频率进行建模，完成对近断层非平稳地震动样本的随机模拟。

本方法事先没有引入任何假设，完全从实测地震动记录数据本身出发，首先通过swt将原始地震动记录分解为多层窄带“子序列”，其次对每一窄带“子序列”依次进行hilbert变换进而得到其瞬时幅值与瞬时频率，通过以上两个步骤获得的瞬时幅值与瞬时频率可为非平稳地震动样本的模拟提供基础，最后利用信号重构技术获得近断层地震动的模拟公式，swt可视为一类特殊的小波分解方法，其使用冗余小波基函数，使原始记录在冗余基函数上的表示可看成是信号在一系列基函数上表示的平均，小波系数和尺度系数与原始记录等长，保证了平移不变性，不仅可以很好地抑制二进小波变换中的振荡效应，而且部分小波系数的扰动不会带来信号的严重失真，从而减小了信号的重构效果对单个小波系数的依赖，所以采用swt进行地震波分解与重构方面具有较好的优势，从而提高了样本模拟的精度。

进一步的，在步骤(1)中，swt以二分频形式将所述原始近断层非平稳地震动记录分解的表达式为：

其中，dj(t)为第j层细节分量，代表高频成分；m为全部分解的层数；am(t)为近似分量，代表低频成分。

进一步的，在步骤(2)中，对于任意所述单分量信号c(t)均通过hilbert变换构造出其复解析信号形式z(t)，

z(t)＝c(t)+ih[c(t)]＝a(t)e^iφ(t)，其中，a(t)与φ(t)分别表示随时间变化的幅值与相位；h(·)算子表示hilbert变换，其中，s为积分变量；p代表柯西主值；

进一步的，瞬时幅值为瞬时相位为φ(t)＝tan^-1{h[c(t)]/c(t)}，瞬时频率为

进一步的，对所述近断层非平稳地震动样本的随机模拟公式为：

其中，为服从于高斯分布的第j阶分量的瞬时频率，即φj为第j阶[0,2π]均匀分布的随机初始相位角。

进一步的，还包括步骤(4)，所述步骤(4)为采用优化理论算法调整所述近断层非平稳地震动样本，使其与目标反应谱匹配。

进一步的，步骤(4)包含如下步骤：

(4-1)通过公式调整每一阶所述单分量信号的幅值和频率，其中，x1,x2,…,xn为地震动幅值分量的调整系数；xn+1,xn+2,...,x2n为地震动频率分量的调整系数；x＝{x1,x2,…,x2n}^t为调整系数向量；m为全部分解的层数；am(t)为近似分量；

(4-2)建立多变量优化理论模型，其公式为：

minimize:约束条件为：xj＞0,j＝1,2,…,2n，其中，s[y(x,t),tp]为模拟样本在指定的特征周期tp时的反应谱值，st(tp)为周期为tp时的目标反应谱值；p为反应谱周期离散点的数目；v为建立的目标函数；

(4-3)采用非线性拟牛顿算法求解所述目标函数v的最小化问题，即可实现模拟样本与目标反应谱的匹配。

与现有技术相比，本发明的有益效果：本发明采用swt使用冗余小波基函数，使原始信号在冗余基函数上的表示可看成是信号在一系列基函数上表示的平均，小波系数和尺度系数与原始信号等长，保证了平移不变性，不仅可以很好地抑制二进小波变换中的振荡效应，而且部分小波系数的扰动不会带来信号的严重失真，从而减小了信号的重构效果对单个小波系数的依赖，所以采用swt进行地震波分解与重构方面具有较好的优势，并能保证样本模拟的精度，现有技术中，带有近断层特性的人工波很难实现与目标反应谱的匹配，因此在上述模拟方法的基础上，为了进一步使得由原始近断层地震动模拟得到的样本与目标反应谱匹配，通过引入多个变量来调整每一单分量的幅值和频率大小，接着建立优化理论模型并采用非线性拟牛顿法算法迭代求解，即可实现了与目标反应谱的匹配相容。本发明方法不仅在分解与重构方面的技术优势能够显著提高样本模拟的精度，而且建立的优化模型更容易实现与目标反应谱匹配的工程抗震要求，有利于提高工程结构抗震时域分析的可靠度，本发明方法还可适用于中、远场一般地震动的随机模拟，具有普遍的适用性。

附图说明

图1为本发明中与反应谱匹配的近断层非平稳地震动模拟方法的流程图。

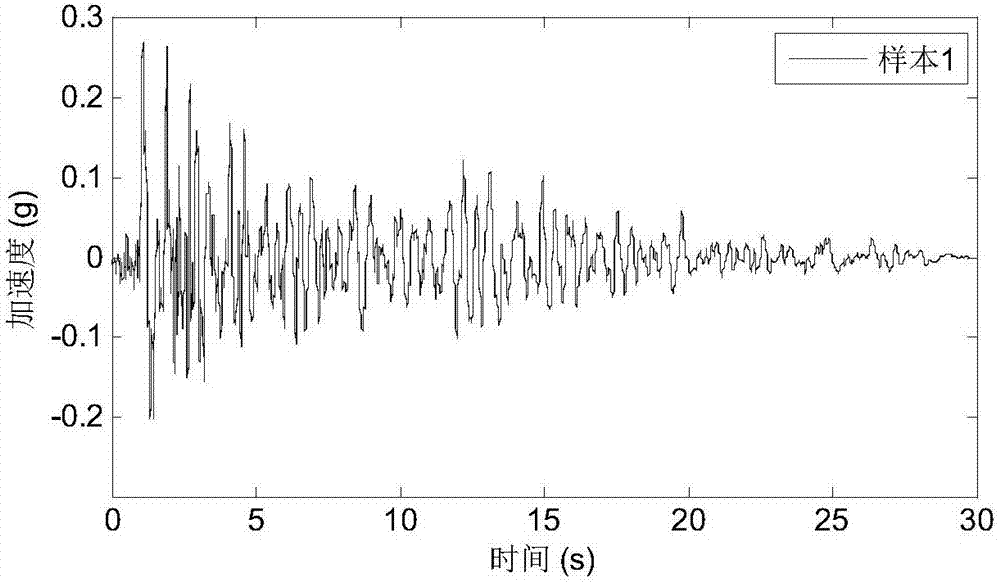
图2a、图2b和图2c分别为实施例1中所用到的三组实测近断层地震动样本记录。

图3a为实施例1中图2a的细节分量。

图3b为实施例1中图2a的近似分量。

图4为实施例1中地震动样本1第一阶分量的瞬时频率分布及其高斯分布拟合。

图5为实施例1中调整前与目标反应谱的对比图。

图6a为实施例1中地震动样本1的非平稳时-频特征。

图6b为实施例1中由地震动样本1模拟生成样本的非平稳时-频特征。

图7为实施例1中调整后与目标反应谱的对比图。

图8a、图8b和图8c分别为实施例1中与目标反应谱匹配的三组模拟样本。

具体实施方式

下面结合实施例及具体实施方式对本发明作进一步的详细描述。但不应将此理解为本发明上述主题的范围仅限于以下的实施例，凡基于本发明内容所实现的技术均属于本发明的范围。

实施例1

一种基于数据驱动的近断层非平稳地震动模拟方法，如图1，包括如下步骤：

(1)通过swt将原始近断层非平稳地震动记录分解为若干个单分量信号的叠加；

(2)分别对每一阶所述单分量信号利用hilbert变换得到其瞬时幅值与瞬时相位，并根据所述瞬时相位求得瞬时频率；

(3)利用均匀分布的初始相位角以及高斯分布的瞬时频率进行建模，完成对近断层非平稳地震动样本的随机模拟；

(4)采用优化理论算法调整所述近断层非平稳地震动样本，使其与目标反应谱匹配。

为了方便说明，我们以实测的近断层地震动样本为例，图2a、图2b和图2c所示为实测的近断层地震动三组样本，采样频率为fs＝100hz，采样时长为t＝30s，对上述原始近断层非平稳地震动记录样本进行swt分解，表达式为：

其中，dj(t)为第j层细节分量，代表高频成分；m为全部分解的层数；am(t)为近似分量，代表低频成分，由于近似分量最高频率根据fs/2^j+1确定，j为分解层数，当分解层数取为8时近似分量的最高频率仅为0.19hz，所以可以用来较好地表示原始地震动记录的趋势项。

以样本1为例，8层细节分量和近似分量分别如图3a和图3b所示，然后采用hilbert变换构造出其复解析信号形式z(t)，z(t)＝c(t)+ih[c(t)]＝a(t)e^iφ(t)，其中，a(t)与φ(t)分别表示随时间变化的幅值与相位；h(·)算子表示hilbert变换，其中，s为积分变量；p代表柯西主值；瞬时幅值为瞬时相位为φ(t)＝tan^-1{h[c(t)]/c(t)}，瞬时频率为

然后利用均匀分布的初始相位角以及高斯分布的瞬时频率进行建模，其中，为第j阶分量的瞬时频率，它是服从高斯分布的随机变量，即φj为第j阶[0,2π]均匀分布的随机初始相位角，如图4所示。

上述基于数据驱动的近断层非平稳地震动样本的模拟结果，如图5，可以观察到，原始非平稳样本与模拟样本具有一致的非平稳时-频特征，如图6a与图6b。表明本模拟方法结果可靠。

然而根据图5可以看出，由上述swt+hilbert变换模拟样本得到的反应谱曲线常与目标反应谱存在一定偏差，通过模拟公式：

调整每一个所述单分量信号的幅值和频率，其中，x1,x2,...,xn为地震动幅值分量的调整系数；xn+1,xn+2,...,x2n为地震动频率分量的调整系数；x＝{x1,x2,...,x2n}^t为调整系数向量；m为全部分解的层数；am(t)为近似分量。

通过构造2n个调整系数建立多变量优化理论模型，其公式为：

minimize:约束条件为：xj＞0,j＝1,2,…,2n，其中，s[y(x,t),tp]为模拟样本在指定的特征周期tp时的反应谱值，st(tp)为周期为tp时的目标反应谱值；p为反应谱周期离散点的数目；v为建立的目标函数；采用非线性拟牛顿算法求解所述目标函数v的最小化问题，即可实现模拟样本与目标反应谱的匹配，如图7，最终获得与目标反应谱匹配的三组模拟样本，如图8a、图8b和图8c。