高超声速飞行器前缘流‑热‑固一体化计算方法与流程

本发明属飞行器气动计算技术领域，具体指代一种高超声速飞行器前缘流-热-固一体化计算方法。

背景技术：

高超声速流动通常是指马赫数大于5的流动。飞行器以高超声速出入大气层或持续在空间飞行时，由于压缩效应以及飞行器表面与空气的剧烈摩擦(王江峰，伍贻兆，季卫栋，樊孝峰，赵法明，吕侦军2015《航空学报》36(1):159-175“高超声速复杂气动问题数值方法研究进展”)，飞行器头部、进气道前缘等关键部位将承受巨大的气动加热，会产生强烈的气动力、气动热及结构耦合问题，对飞行安全带来极大隐患。因此准确预测+气动加热与结构传热的物理过程，对高速飞行器的热防护系统轻量化设计，起到重要作用。由于此类问题的地面实验难度高、周期长，因此目前对此类问题的分析主要还是采用数值模拟技术。

目前，高超声速飞行器气动热/结构传热耦合问题的数值模拟主要分为分区耦合计算和一体化求解两种方法。传统的多场分区耦合方法(夏刚，刘新建，程文科，秦子增2003《国防科技大学学报》25(1):35-39“钝体高超声速气动加热与结构热传递耦合的数值计算”；姚小虎，韩强2008《物理学报》57(8):5056-5062“热力耦合作用下双层碳纳米管的扭转屈曲”)将流场和结构划分为独立的两个部分，以时间域上的耦合交替迭代方式，在耦合交界面上进行流场热流密度与结构表面温度两个参数的数据交换。nasa兰利研究中心的dechaumphi(wietingar,dechaumphaip,beyks1991thinwall.struct.11112)认为分区耦合方法的数学模型需要额外的数据传递策略，且将本来连续的物理过程人为划分，从而产生计算误差，会对计算结果准确性产生影响。

一体化求解方法的思想在上世纪70年代末被提出，国内外研究人员也有一些研究成果。thornton(dechaumphaip,thorntonea,wietingar1989j.spacecraft26201209)教授等于1988年采用有限元方法对流场与固体结构进行一体化求解研究，并在8英尺的nasa兰利高焓风洞进行二维圆管气动加热试验(allenrw1987nasatm-100484)，验证了该方法有效性，但是由于有限元方法离散过程仍然只是采用简单的插值方法，使得计算时在激波等间断处出现明显的非物理震荡，激波分辨率较低，导致需要通过在激波处加密网格来捕捉激波，计算方法灵活性较差，应用受到限制。北京空气动力研究所黄唐等(黄唐，毛国良，姜贵庆，周伟江2000《空气动力学报》18(1):115-119“二维流场、热、结构一体化数值模拟”)对二维流场、热、结构一体化数值模拟开展了相关研究，流场采用基于tvd格式的有限差分法进行数值离散，结构传热采用成熟的有限单元方法，两者在耦合交界面满足能量平衡方程，但由于在流场与结构时间步长的数量级上的差异导致耦合计算量与计算误差大等问题。他们认为要真正在工程上实现流场、热、结构的一体化计算，必须扩展流场、热、结构的一体化数值计算概念，满足流场、热、结构连续整体的物理变化条件，才能保证热结构的计算精度。另外，姜贵庆等(姜贵庆，童秉纲，曹树声1992《力学与实践》14(3):1-8“以有限元方法为主体的计算气动热力学”)认为随着航天技术与气动热力学的发展与深化，现代气动热力学必须解决气体-热-结构的三位一体化的求解问题，分析了有限单元法求解该问题的优势，同时也说明强间断问题在有限元法中尚未得到良好解决。中国空气动力研究与发展中心的耿湘人等(耿湘人，张涵信，沈清2002《空气动力学报》20(4):422-427“高速飞行器流场和固体结构温度场一体化计算新方法的初步研究”)基于levelset方法将不同介质的气体流场与固体结构统一到同一控制方程，采用差分方法进行数值离散计算，对二维、三维模型进行数值计算验证，结果表明与实验值吻合良好。该方法忽略了特征时间较小一方的时间变化细节，存在求解的刚性问题，并且对复杂气动外形的计算适应性有待改善。

技术实现要素：

针对于上述现有技术的不足，本发明的目的在于提供一种高超声速飞行器前缘流-热-固一体化计算方法，以解决传统气动加热/结构传热耦合求解方法在时间域内进行流场与结构耦合交替迭代计算所带来的繁琐数据交换与计算量的问题。

为达到上述目的，本发明采用的技术方案如下：

本发明的一种高超声速飞行器前缘流-热-固一体化计算方法，包括步骤如下：

将流场与结构作为同一个物理场，同时计算流场与结构的物性参数与热力学性质，将流场与结构交界面作为整个物理场的内部边界，联立流场与结构传热控制方程，采用统一数值计算方法同时求解。

优选地，对于结构传热，在控制体ωs上结构传热控制方程积分形式如下，不考虑热源：

式中，ds为控制体面单元，cs为固体材料比热容，t为结构温度，为温度梯度，ρ为材料密度，k为导热系数，为边界；流场计算采用可压缩雷诺平均n-s(rans)方程，在控制体ωs上，将流场控制方程与结构传热控制方程统一到同一积分形式的控制方程中：

式中，w为守恒量，fc为对流通量，fv为粘性通量；其定义如下：

对于流场计算，密度ρ、压强p和温度t满足理想气体状态方程p＝ρrt，u、v、w分别为控制体三个方向的速度，e为流体单元控制体的总能量，h为总焓h＝e+p/ρ，k为导热系数，τij为粘性应力张量，对于结构传热计算，结构无变形满足u＝v＝w＝0，上式对流通量为零fc＝0，其中e＝cst为固体单元控制体内；

湍流模型选取sstk-ω两方程模型，该模型不需要阻尼函数，能较好模拟近壁面湍流的发展，在边界层粘性干扰强烈区域得到应用，同时因为其可以更好模拟自由剪切层，在远离壁面的湍流中得到应用；空间离散时对流通量采用基于格心格式的ausm+格式进行离散，黏性通量离散采用二阶中心差分格式。为了加速计算，时间离散时，非定常计算采用是双时间隐式时间迭代，定常计算采用lu-sgs隐式时间迭代。

优选地，所述计算方法包含以下边界条件：

(1)流场远场边界条件，其采用riemann边界条件；

(2)物面边界条件，其包括固体表面流动边界条件与热力学边界条件；

a.固体表面流动交界面边界条件满足无滑移边界条件，以及压强梯度为零；

b.结构热传导边界条件为热力学边界条件，其包含dirichlet温度边界条件与neuman热流密度边界条件。

优选地，所述计算方法还包含：交界面温度计算采用中心平均方法计算，如下：

t＝(tl+tr)/2

式中，tl、tr分别为交界面左右控制单元的温度；温度梯度▽t的计算需要进行修正，计算方法如下：

式中，分别为交界面左右控制单元的温度梯度，llr为单元中心之间的距离，rlr为左控制单元中心点到右控制单元中心点的单位向量；此外，温度梯度的计算方法采用高斯格林方法，高斯格林法通过单元的边界的值及法向量来计算：

对于格心格式，即为：

式中，ω为控制体体积，i为单元编号，j为相邻单元编号，nij为单位法向向量，δsij为控制体表面积，n为控制体单元面编号；为了提高计算的准确性，引入固体传热中热阻抗的概念，定义热阻抗为：

式中，d为热流方向的厚度，a为垂直于热流方向的截面面积，k为导热系数；通过引入热阻抗的概念得到交界面的热阻抗关系式：

rt,bnd＝rt,l+rt,r

得到交界面导热系数k计算式子如下：

其中，kl、kr分别为左右控制单元的热传导系数，ll、lr分别为左右控制单元中心到边界中心的距离。

本发明的有益效果：

本发明避开传统气动加热/结构传热耦合求解方法在时间域内进行流场与结构耦合交替迭代计算所带来的繁琐数据交换与计算量，将流场与结构作为一个物理场，采用统一的控制方程。对流固交界面的物性参数进行重新定义，全物理场进行有限体积方法空间离散，时间推进采用隐式时间迭代。采用典型高超声速绕流二维圆管稳态/非稳态流-热-固耦合算例对该一体化计算方法进行验证，得到稳态时圆管驻点温度最高达到648k，非稳态下的热流密度和结构温度与参考文献和实验值吻合较好，证明了该方法的可靠性和正确性。同时与耦合计算方法的对比分析结果表明，本发明的一体化计算方法所得计算结果更接近实验值，并且计算量和网格依赖性都相对较小，具有更好的稳定性和计算精度。

附图说明

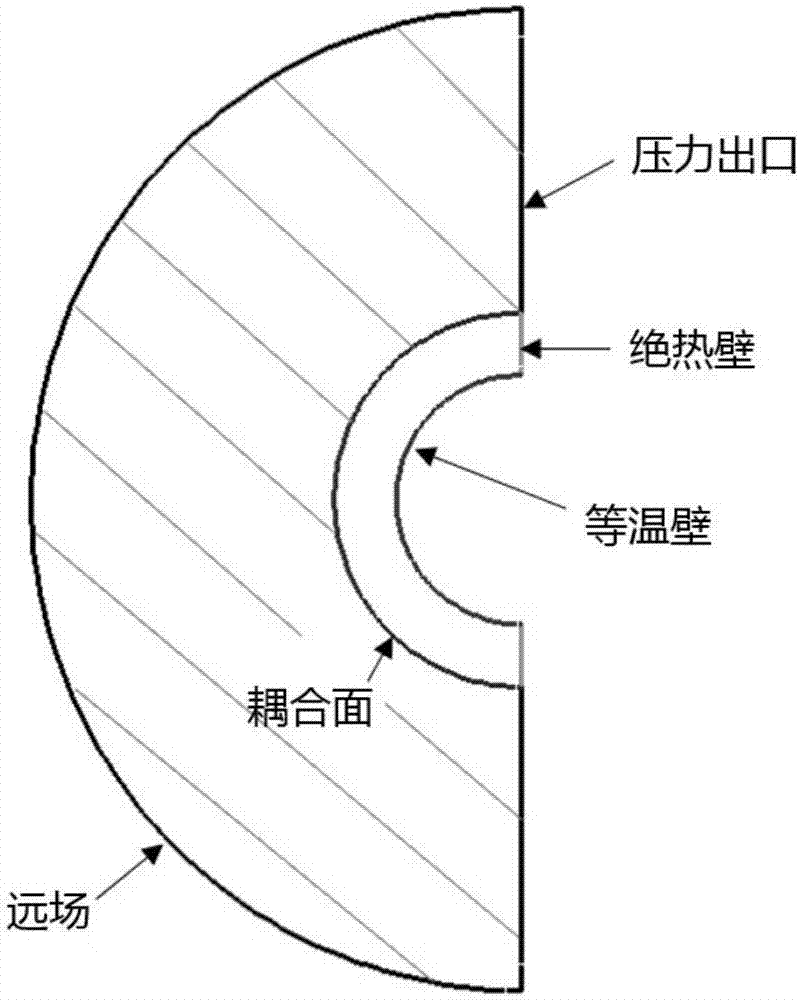
图1a为计算网格示意图。

图1b为边界条件示意图。

图2a为圆管结构温度分布示意图。

图2b为流场温度分布示意图。

图3a为密度等值线图与试验纹影图对比示意图。

图3b为圆管表面压强分布与试验值对比示意图。

图4a为第0.1s时圆管结构温度云图。

图4b为第0.5s时圆管结构温度云图。

图4c为第1.0s时圆管结构温度云图。

图4d为第2.0s时圆管结构温度云图。

图5为圆管驻点温度随时间变化示意图。

图6为第2s时圆管结构温度分布与文献对比示意图。

图7a为第0.1s时流场温度云图。

图7b为第0.5s时流场温度云图。

图7c为第1.0s时流场温度云图。

图7d为第2.0s时流场温度云图。

图8为不同时刻流场沿对称线温度变化示意图。

图9为第0s时圆管表面热流分布对比示意图。

图10为驻点热流随时间变化示意图。

图11为串行耦合迭代方法示意图。

图12为耦合求解方法计算流程图。

图13a为驻点温度随时间变化示意图。

图13b为温度差随时间变化示意图。

图14为流-热-固耦合问题物理模型示意图。

具体实施方式

为了便于本领域技术人员的理解，下面结合实施例与附图对本发明作进一步的说明，实施方式提及的内容并非对本发明的限定。

1、技术参数

wieting.a.r(allenrw1987nasatm-100484)于1987年在美国nasa兰利研究中心的8英尺的高焓风洞完成了不锈钢圆管前缘气动加热试验(wietingar,holdenms1987aiaa22ndthermophysicsconferencehonoluluhawaiijune8-10,1987)，该试验已经被多次用于验证流场结构传热耦合计算的准确性。本发明同样选取条件完全相同的无限长不锈钢圆管模型，圆管尺寸为外径rout＝0.0381m，内径rin＝0.0254m，结构材料为aisi321系列(1crl8ni9ti)不锈钢。其热力学参数见表1，来流条件计算参数在表2中给出，如下：

表1

表2

2、模型网格

流场计算与结构计算为同一套网格，图1a，流场网格量约为37100，结构网格量约为3800，近物面第一层网格高度约为1×10^-6m。图1b为边界条件，流场两端为压力出口边界条件，圆管两端为绝热壁，内壁为等温壁，圆管初始温度为294.4k。

3、数值模拟结果

对不锈钢材质圆管开展高超声速流-固-热一体化定常与非定常数值计算，其中非定常状态，真实计算物理时间为2s，真实时间步长取δt＝0.001s。

3.1稳态状态结果分析：

图2a给出了稳态时圆管的结构温度分布，由图看出，稳态时圆管结构高温区分布在驻点区域，驻点区温度最高为648k，温升到达353.6k，内壁温度由初始294.4k升高到305k，相比内壁温升很小为10.6k。图2b给出了稳态时圆管外的流场温度分布，流场经过弓形激波加热后，流场最高温度达到2263k。图2a，图2b很好展示了本发明方法的优势之一就是可以较快计算出稳态结构与流场的温度分布，很好解决了高超声速流-固-热稳态求解问题。目前的耦合计算方法是在流场和结构交界面上进行热流与温度的参数交换，若求解稳态时流场与结构的温度分布时，必须进行多次迭代，直至结构的温度收敛，反复的流场与结构的迭代，带来极大的计算量，本发明的一体化计算方法进行全物理场迭代，可以很好规避参数的交换。

图3a是计算得到的密度等值线图与试验纹影图对比，上半部分为试验纹影照片，下半部分为密度云图(dechaumphaip,thorntonea,wietingar1989j.spacecraft26201209)，对比发现激波位置基本吻合。同时，图3b给出了圆管表面压强分布(归一化)与试验值的对比，压强沿圆管的分布和试验值重合度较好，由此说明了稳态流场计算的正确性。

3.2非稳态结构温度场特性分析：

图4给出了非稳态计算中圆管结构在不同时刻(t＝0.1s、0.5s、1.0s、2.0s)温度分布云图。从图中可以明显看出2秒内圆管结构内温度分布的变化，随着时间的推进，气动加热产生的热量在结构内传导，结构整体温度升高，高温区域从驻点区域开始逐渐增大，且驻点温度始终最高。2秒内，驻点温度从294.4k升高到390.2k，比dechaumphai所计算的388.8k略高，误差在0.4％左右，同时圆管内壁温度基本保持初始温度294.4k，说明2秒内气动加热引起的结构热响应暂未影响结构内壁面。

图5给出圆管驻点温度随计算时间的变化，并与参考文献进行了对比，计算结果与参考文献(黄杰2013硕士学位论文高超声速飞行器流热固多物理场耦合计算研究，哈尔滨工业大学)吻合良好，2s时驻点温度最大误差为3.2k，详见表3。从图中可以看出，初始时刻驻点温度升高剧烈，随着时间的推进，温升程度逐渐趋于平缓，这是由于初始时刻驻点热流最大，随着热量在结构中的传递，结构温度升高，驻点热流率逐渐下降，温升趋势逐渐减小。表3如下：

表3

表3中，文献1：耿湘人，张涵信，沈清2002空气动力学报20422；文献2黄杰2013硕士学位论文高超声速飞行器流热固多物理场耦合计算研究，哈尔滨工业大学；文献3：dechaumphaip,thorntonea,wietingar1989j.spacecraft26201。

为了更好分析计算方法的准确性，图6给出了t＝2s时圆管温度分布等值线的对比图，上半部分为参考文献结果，下半部分为本发明计算结果，可以看出计算结果与文献结果吻合较好。

3.3非稳态流场特性分析：

图7a-图7d为不同时刻驻点区域流场温度等值线图，图8为不同时刻沿对称线(y＝0)流场温度变化曲线。从图中可以看出，来流通过弓形激波加热后，温度从241.5k急剧升高到2163k，与上述文献2的2166.7相差不大。从图中可以看出弓形激波的位置大概在-54.5mm左右，与完全气体状态下经验公式(billigfs1967j.spacecraft4822)计算得到的-54.5mm吻合较好，说明本发明计算条件不考虑化学非平衡效应是合理的。靠近驻点附近存在温度边界层区域，该区域的厚度约为弓形激波厚度的3％左右，温度边界层中存在较大的温度梯度，温度从2163k急剧下降到294.4k，因此在驻点区域产生较大的热流密度。

图9为初始时刻(t＝0)圆管表面热流分布与试验值的对比，本发明的热流计算分布结果(归一化处理)与实验值吻合一致。初始时刻的热流值在驻点处最大，计算所得最大热流49.71×10⁴w/m²，略高于fay-riddell(fayja,riddellfr1958journaloftheaeronauticsciences257385)公式计算得到48.27×10⁴w/m²和粘性激波层公式(holcombje,curtisjt,shopefl1985tnaedc-tmr-85-v7)计算得到47.02×10⁴w/m²，但是远小于实验值70.07×10⁴w/m²，由于热流计算对来流湍流度比较敏感，这种差异可能是目前暂未考虑实验来流的湍流度与计算来流状态的差异所引起的，具体的数值对比详见表1。表3为2s时刻驻点温度和初始时刻热流值与参考文献的对比。图10为驻点热流随时间变化曲线，可以看出随时间推进，驻点热流逐渐降低，而且下降趋势逐渐平缓，这是由于热量的在圆管结构中的传导，驻点温度逐渐升高，温度边界层内的厚度增厚，温度梯度逐渐减小，热流密度因此逐渐降低，2s时热流密度较初始时刻下降约6.3％，与文献中2s内热流下降8％接近。

本发明的计算方法与耦合求解的相互比较

气动加热/结构传热耦合求解方法(聂涛，刘伟强2012《物理学报》61184401“高超声速飞行器前缘流固耦合计算方法研究”)是在时间域内流场与结构交替迭代的计算方法。主要分成以下两个过程：一是将交界界面的物面温度作为流场边界条件计算流场，得到交界边界的热流密度；二是将热流密度作为结构边界条件来计算结构的温度场。

耦合求解方法的时间迭代计算流程如图11，该耦合方案为串行迭代耦合方案，该方案是建立在结构传热的特征时间远大于流场特征时间且传热是一个慢变过程的基础上，那么与结构传热计算相比，可以假设流场是瞬态稳定的，结构与流场只在真实时间节点上进行数据交换。

针对上述耦合迭代方法，图12给出耦合求解方法计算流程图，其中在每个真实物理时间步内对流场和结构进行一次数据交换，计算流程如下：

(1)将ti物理时刻的边界温度分布ti传递给流场网格；

(2)流场内进行伪时间迭代，直到收敛；

(3)计算ti物理时刻流场边界热流插值qi；

(4)将热流插值qi传递到结构网格；

(5)ti时刻结构瞬态传热进行伪时间迭代，直到收敛；

(6)判断是否达到计算要求，如果达到则程序结束，否则ti＝ti+δt，返回(1)。

通过加热时间2s的非定常气动加热算例来对比耦合算法和本发明计算方法的计算准确度和网格敏感性(阎超，禹建军，李君哲2006《空气动力学报》24(1):125-130“热流cfd计算中格式和网格效应若干问题研究”；潘沙，冯定华，丁国昊2010《航空学报》31(3):493-499“气动热数值模拟中的网格相关性及收敛”)。计算时间步长0.001s，计算总时间为2s。分别取两套不同的网格，第一套网格交界面处流场网格尺度和结构网格尺度均为1×10^-6m，第二套网格交界面处流场网格尺度和结构网格尺度均为5×10^-5m。

图13a为不同网格尺度时的驻点温度随时间变化曲线，图13b为在两种算法计算出的温度差随时间的变化曲线。从图13a，13b中可以看出，网络细分时两种算法的计算结果基本重合，2s时的驻点温度约388k，说明在该网格尺度下，两种算法计算结果均合理。而当网络粗分时两种算法的计算结果差别很大，本发明计算方法2s时的驻点温度约388k，计算结果正确；耦合算法2s时的驻点温度不到360，计算结果不合理。这两个算例的计算结果表明，本发明的计算方法对网格尺度的依赖性小于耦合算法，具有较高的网格适应性。图13a，13b中，耦合算法和本发明的计算方法的驻点温度差初期变化剧烈，随着时间的推移快速减小，最后趋于不变。传热初期本发明的计算方法计算得到的驻点温度值小于耦合算法计算得到的驻点温度值，后期则本发明的计算方法计算的值大于耦合算法计算的值。原因是初始迭代时耦合算法计算时是假定了一个交界面驻点温度值，然后计算流场，得到交界面热流，此时得到的驻点热流值相对真实热流值偏大。而本发明的计算方法中，交界面的驻点温度值是实时计算出来的，因此得到的驻点热流值更接近真实热流。这样，传热初期本发明的计算方法计算出的驻点温度值将低于耦合算法得到的驻点温度值。接下来的迭代中，必然会出现耦合算法得到的驻点热流值小于本发明的计算方法得到的驻点热流值。从而使得本发明的计算方法计算出的驻点温度高于耦合算法得到的驻点温度值。

本发明的计算方法对网格尺度依赖小于耦合算法的主要原因是本发明的计算方法中流场与结构的交界面上的温度、温度梯度及传热系数由流场与结构内近物面参数插值得到，而耦合算法中的交界温度和热流计算仅与流场或结构有关。

本发明具体应用途径很多，例如图14，以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明原理的前提下，还可以作出若干改进，这些改进也应视为本发明的保护范围。