大规模埋地油气管道GIC和PSP计算方法与流程

本发明涉及埋地油气管道自然灾害防御技术领域，具体涉及一种基于广义对称分量的直流有源电路等效的大规模埋地管道gic和psp计算方法。

背景技术：

由于现场实际大规模埋地油气管道纵横交错，其等效电路也就会错综复杂，另外，由于受地磁暴影响后的等效电路是有源分布的。这样，埋地油气管道网络含分布源等效电路模型就会更加复杂，而且，网络规模极其庞大，就给埋地油气管道gic和psp的计算带来困惑。解决问题的途径在传统上一般有回路电流方法和节点电压方法两种方法。在回路电流方法中，研究发现，由于埋地油气管道网络的大规模特征使回路电流方法回路方程阶数增多，从而使求解gic(地磁感应电流gic，geomagneticallyinducedcurrent)和psp(干扰管地电位psp，pipetosoilpotential)的计算收敛速度变得太慢，当高阶代数方程阶数过多时，会导致仿真计算有时甚至不能求出真解或导致算法根本无法给出收敛的计算结果。同样，在节点电压方法中，研究发现，存在与回路电流方法同样的问题，埋地油气管道网络的大规模特性使节点电压方法中的节点方程阶数增高，从而使求解gic和psp的计算收敛速度变得太慢，当高阶代数方程阶数过多时，会导致仿真计算有时甚至不能求出真解或导致算法根本无法给出收敛的计算结果。

为了能够利用传统回路电流方法和节点电压方法求解大规模埋地油气管道网络的gic和psp，必须对大规模埋地油气管道网络等效电路进行降阶化简处理。已有方法有两种：对于单端固定的放射状电路，应用戴维南定理或诺顿定理等效方法比较有效；对于双端固定的闭合电路回路，一般应用y－△型联结电路变换方法效果较好。

在单端固定的放射状电路的戴维南定理或诺顿定理等效方法中。对于线性的埋地油气管道等效电路，为解决其大规模gic和psp计算问题，以往的传统解决办法是：首先从电路中选择所要计算gic和psp的管道及其所对应等效电路，然后，从电路首端或末端开始，通过使用戴维南定理或诺顿定理迭代等效电路来进行等效，得到简化电路(包含所选择的要计算的管道gic和psp所对应等效电路)并求解得到所选择管道的gic和psp结果，从而，同理进一步可以使大规模电路可求解并能够提高求解速度。但是，如果要考虑埋地油气管道电路中所含的阴极保护装置或非线性的去耦合器等对埋地油气管道电路的影响时，尽管埋地油气管道电路是线性非实变的，但是，由于阴极保护装置或非线性的去耦合器等的非线性模型特性，叠加原理已不再适用，对其非线性电路进行等效是极其困难的甚至是不可能的。因此，在其gic和psp仿真计算过程中，只能对线性电路进行等效，使用戴维南定理或诺顿定理迭代法则对非线性电路进行等效面临了叠加原理不适用的挑战。这样，在单端固定的放射状电路的求解过程中，为化简电路就必须尝试寻找从两端受限电路内任意一点开始对电路进行迭代等效方法，其问题的核心是双端固定的闭合线性电路等效问题。

申请人研究发现，在双端固定的闭合线性电路的有源y－△型联结电路变换方法中，对于大规模复杂回路电路，可以对不十分关心的部分电路进行等效化简，对关心的部分电路保留，这样通过简化电路可得到所关心电路的gic和psp分布解。但是，在研究地磁暴对所关心的阴极保护装置或非线性去耦合器的影响时，阴极保护装置或非线性去耦合器的位置必须保留不变。这样，在仿真计算中就必须有方法解决对任意一段电路进行等效的方法。而使用放射状电路的戴维南定理或诺顿定理等效方法是行不通的。很自然，y－△型联结电路变换方法会被应用去解决所遇到的问题。这就是在常规直流电路求解过程中所使用的y型－△型联结电路变换方法。但是，常规直流电路y－△型联结电路变换方法解决的是无源电路问题。在有源直流电路中进行y－△型联结电路变换方法研究中，研究表明，求解大规模复杂回路电路碰到了“有源直流电路y－△型联结电路变换变换方法”无法求解的难题。到目前为止，尚未见到该问题具体解决方案的报道。

综上所述，要想求解大规模埋地油气管道gic和psp问题，必须解决一段埋地油气管道等效电路简化变换方法，解决一段埋地油气管道等效电路简化变换方法的关键问题是能够在有源电路中实现有源y—△型联结电路变换电路的正变换和逆变换。

技术实现要素：

为了解决现有技术中含非线性电路的大规模埋地油气管道gic和psp求解所存在的难题，本发明提供一种基于广义对称分量的直流有源电路等效的大规模埋地管道gic和psp计算方法。

本发明采用如下技术方案。

一种大规模埋地油气管道gic和psp计算方法，该方法包括：

第一步，将大规模埋地油气管道等效电路分成若干部分；

第二步，选取大规模埋地油气管道等效电路的若干部分之一，保留其非线性电路部分，利用有源y—△型联结电路变换正变换和有源y—△型联结电路逆变换，对大规模埋地油气管道等效电路的其余部分进行等效电路变换实现简化，从而将高阶大规模埋地油气管道等效电路变成低阶埋地油气管道等效电路；

第三步，利用回路电流方程或节点电压方程求解低阶埋地油气管道等效电路gic和psp；

第四步，将大规模埋地油气管道等效电路的若干部分的每一部分都分别扫描计算一遍，集成若干部分的计算结果就得到大规模埋地油气管道gic和psp全部结果。

优选的是，利用回路电流方程求解低阶埋地油气管道等效电路gic和psp，所述大规模埋地油气管道gic和psp的回路电流计算方法包括：

第一步骤，给定计算机及其算法所能计算的最多回路数(回路数是指使用回路电流法求解直流电路电流和电压所定义的回路数)，用符号mloop表示；

第二步骤，给出被研究管网对象和与其对应的整体等效电路(以下简称原电路)；

第三步骤，将电路中的非线性元件和关键节点部分电路定义保留标记，其回路数用符号kloop表示，即，除保留电路外，电路的其余部分均为线性电路；

第四步骤，将原电路进行划分得到n段原电路，在n段原电路中的每段原电路的回路数为lloop，其约束条件为：lloop+kloop＜mloop，算法能够求出正确解；

第五步骤，选取初值：i＝1；

第六步骤，提取第i段原电路；这里欲仿真计算该第i段埋地油气管道对应电路的gic和psp分布；

第七步骤，对j＝1、2、…i-1、i+1、…、n(其中j≠i)段原电路分别使用“一段埋地油气管道的等效变换方法”对之线性电路进行等效变换，将非线性元件和关键节点部分电路保留，分别得到对应的n-1段等效电路；

第八步骤，将等效后的电路称为第i段等效电路；将第i段原电路及其相连接的等效后的电路统称为第i段电路“后等效电路”；

第九步骤，利用回路电流方法仿真计算第i段后等效电路的gic和psp分布，保存第i段原电路的gic和psp分布结果；

第十步骤，判断：

如果i＜n，则变量i递增i＝i+1，转第七步骤，继续计算；

如果i＝n，输出i＝1、2、3……n段原电路的gic和psp分布结果，就是被研究管网对象的gic和psp分布结果；

第十一步骤，结束计算。

在上述任一技术方案中优选的是，利用节点电压方程求解低阶埋地油气管道等效电路gic和psp，所述大规模埋地油气管道gic和psp的节点电压计算方法包括：

第一步骤，给定计算机及其算法所能计算的最多节点数(定义节点数：指使用节点电压法求解直流电路电流和电压所定义的节点数)，用符号mnod表示；

第二步骤，给出被研究管网对象和与其对应的整体等效电路(以下简称原电路)；

第三步骤，将电路中的非线性元件和关键节点部分电路定义保留标记，节点数，用符号knod表示，即，除保留电路外，电路的其余部分均为线性电路；

第四步骤，将原电路进行划分得到n段原电路，在n段原电路中的每段原电路的节点数lnod，其约束条件为：lnod+knod＜mnod，算法能够求出正确解；

第五步骤，选取初值：i＝1；

第六步骤，提取第i段原电路；这里欲仿真计算该段埋地油气管道对应电路的gic和psp分布；

第七步骤，对j＝1、2、…i-1、i+1、…、n(其中j≠i)段原电路分别使用“一段埋地油气管道的等效变换方法”对之线性电路进行等效变换，将非线性元件和关键节点部分电路保留，分别得到对应的n-1段等效电路；

第八步骤，将等效后的电路称为第i段等效电路；

第九步骤，利用节点电压方法仿真计算第i段等效电路的gic和psp分布，保存第i段原电路的gic和psp分布结果；

第十步骤，判断：

如果i＜n，则变量i递增i＝i+1，转第七步骤，继续计算；

如果i＝n，输出i＝1、2、3……n段原电路的gic和psp分布结果，就是被研究管网对象的gic和psp分布结果；

第十一步骤，结束计算。

在上述任一技术方案中优选的是，利用有源y—△型联结电路变换正变换和有源y—△型联结电路逆变换，对大规模埋地油气管道等效电路的其余部分进行等效电路变换实现简化，所述有源y—△型联结电路正变换算法包括：

进行有源电阻网络的等效变换，有源y(对称或不对称y型)联结电路→对称△型联结电路变换被定义为有源y—△型联结电路正变换算法，同无源y—△型联结电路网络构造一样，有源y—△型联结电路变换网络，分别标注出相应端号，流经三个端点的电流为i1、i2和i3；端点间的电压为u12、u23和u31；

有源y型联结网络中，e1、e2和e3分别为y型联结支路上的电源电势，r1、r2和r3分别为y型联结支路上与电源电势相对应的的电阻(注：这里电阻参数为非实时变化参数)，并且按规定的正方向；按照基尔霍夫电压定律(kcl)和基尔霍夫电流定律(kvl)推导，有如下关系

由有源y型联结网络方程组解得电流值分别为i1、i2和i3：

对于有源△型联结电路，标注出相应端点处的电流和端点间的电压，e12、e23和e31分别为△型联结电路支路上的电源电势，r12、r23和r31分别为△型联结电路支路上与电源电势相对应的电阻(注：这里电阻参数为非实时变化参数)，设一个参考方向，按照基尔霍夫电压定律(kcl)和基尔霍夫电流定律(kvl)推导得

根据等效变换条件，不论电压u12、u23和u31与电势e1、e2和e3为何值，如果两个电路等效的话，流入对应端子的电流应该相等，对应端子之间的电势应该相等；所以，由y型联结和△型电路联结网络得到的与电流对应的各项应分别相等，即：u12、u23和u31前的系数应该相等，于是得到y型－△型联结电路电阻和电势的等效变换公式分别为

由(5)式看出，由于e12、e23和e31之和为零，所以，无论是对称y型联结和非对称y型联结变换得到的△型联结电路均为对称△型联结电路，这里对称y型电路联结和非对称y型电路联结不作区别。

在上述任一技术方案中优选的是，利用有源y—△型联结电路变换正变换和有源y—△型联结电路逆变换，对大规模埋地油气管道等效电路的其余部分进行等效电路变换实现简化，所述有源y—△型联结电路逆变换算法包括有源y—△型联结电路逆变换算法a、有源y—△型电路逆变换算法b。

在上述任一技术方案中优选的是，所述有源y—△型联结电路逆变换算法a包括：

进行有源电阻网络的等效变换，有源对称△型→y型联结电路变换被定义为有源y—△型联结电路逆变换算法a，当有源△型联结电路网络电势e12、e23和e31满足e12+e23+e31＝0时，按照基尔霍夫定律进行对称△－y型联结电路变换，电阻变换公式如下

根据电势等效公式，由于电源代数和为零，(5)式将会线性相关，将会产生无数组解，因此，确定其中一个变换电源，先设定e1的值，再求出其他两个电源值，由(5)式得到

在上述任一技术方案中优选的是，所述有源y—△型电路逆变换算法b包括：

进行有源电阻网络的等效变换，有源非对称△→y型联结电路变换算法被定义为有源y—△型联结电路变换算法b；当等效模型出现非对称△型联结电路需要变换成y型联结电路网络的情况，当有源△型联结电路网络中三电势之和不为零时，电阻按照y－△型联结电路变换公式求得，电源的等效由广义直流对称分量法来进行分析换算，相对应的直流电源的正序、负序和零序分量分别为广义正序分量、广义负序分量和广义零序分量，具体地：

(a)对非对称△型联结电路的直流电源e12、e23和e31进行广义直流对称分量分解：

对直流电源e12、e23和e31进行广义直流对称分量分解，有

其中，ea1、eb1和ec1为广义正序电压源分量，ea2、eb2和ec2为广义负序电压源分量，ea0、eb0和ec0为广义零序电源电压分量；

根据对称分量法，广义正序和广义负序电源电压分量的关系式为

对于△型联结电路而言，设广义零序电源电压分量ea0、eb0和ec0有如下关系

其中，ia0、ib0、ic0和i0分别为对应的广义零序电流源分量；

由(10)式可得

ea0+eb0+ec0＝i0*(r12+r23+r31)(11)，

由(8)式各式相加，可得

ea0+eb0+ec0＝e12+e23+e31(12)，

将(11)式代入(12)式，可得

i0＝(e12+e23+e31)/(r12+r23+r31)(13)，

将(11)式代入(8)式，可得

任意设(14)式中两个变量分别为某数值，取ea1和eb1分别为不为零某数值，则求得ea2和eb2的表达式为

将(15)式代入(9)式，求得ec1和ec2

至此，在取定ea1和eb1分别为某数值后，利用(15)式和(16)式求得广义正序电源电压分量(ea1、eb1和ec1)和广义负序电源电压分量(ea2、eb2和ec2)；利用(10)式和(13)求得广义零序电源电压分量(ea0、eb0和ec0)；

(b)叠加原理：

对非对称△型联结电路的e12、e23和e31进行广义直流对称分量分解，得到广义正序电源电压分量(ea1、eb1和ec1)、广义负序电源电压分量(ea2、eb2和ec2)和广义零序电源电压分量(ea0、eb0和ec0)；利用叠加原理将广义各序电源电压分量变换合成，得到y型联结电路的电源电压

其中，esa1、esb1和esc1为y型联结电路广义正序电源电压分量；esa2、esb2和esc2为y型联结电路广义负序电源电压分量；esa0、esb0和esc0为y型联结电路广义零序电源电压分量；

广义正序电源电压分量，在广义正序电源电压分量(ea1、eb1和ec1)的作用下，根据对称△—y型联结电路变换方法，求广义正序电源电压分量esa1、esb1和esc1；

广义负序电源电压分量，在广义负序电源电压分量(ea2、eb2和ec2)的作用下，根据对称△型—y型联结电路变换方法，求广义负序电源电压分量esa2、esb2和esc2；

广义零序电源电压分量，由于广义零序电压分量施加在△型联结电路侧，无论另一侧接线方式如何，都没有广义零序电流流过(相当于零序电阻为无穷大)，所以，忽略广义零序电源电压分量(ea0、eb0和ec0)的作用影响，即：

ea0＝0、eb0＝0ec0＝0(18)，

将式(18)代入式(17)，得到y型联结电路的等效电源为

电阻变换公式如下

在上述任一技术方案中优选的是，所述一段埋地油气管道的等效变换方法，选取埋地油气管道lzs-dspl模型中一段四孔网络，埋地油气管道参数r11、r12、r13和r14代表埋地油气管道纵向电阻，r21、r22、r23、r24和r25表示涂层横向电阻，r31、r32、r33和r34表示土壤纵向电阻，e11、e12、e13和e14表示埋地油气管道附近电场强度(注：这里电阻参数为非实时变化参数)，简化网孔，将四网孔合并简化成三个网孔，过程如下：

第一步，y→△型联结电路有源网络变换(有源y—△型联结电路正变换算法)；利用有源y型—对称△型联结电路联结变换(有源y—△型联结电路变换算法a)，y－△型联结电路有源网络变换将其中两个网孔进行合并而简化电路，r12、e12、r13、e13和r23三个支路组成一个y型联结网络，经过变换等效成一个新的△型联结电路网络，用r1、e1、r2、e2、r3、e3表示△型联结电路的三个支路，经过变换后，原来的四个网孔变成了五个网孔；

第二步，左△→y型联结电路有源网络变换(采用有源y—△型联结电路逆变换算法；如果△为有源对称△，则采用有源y—△型联结电路逆变换算法a；如果△为有源非对称△，则采用有源y—△型联结电路逆变换算法b)；网孔r32、r22、r3、e3三个支路组成一个△型联结电路网络，经过△－y型联结电路变换等效成y型联结电路网络r1’、e1’、r2’、e2’、r3’、e3’三个支路；

第三步，右△→y型联结电路有源网络变换(采用有源y—△型联结电路逆变换算法。如果△为有源对称△，则采用有源y—△型联结电路逆变换算法a；如果△为有源非对称△，则采用有源y—△型联结电路逆变换算法b)；与上述第二步同理，网孔r33、r24、r2、e2三个支路也等效成一个y型联结网络r1″、e1″、r2″、e2″、r3″、e3″三个支路；

第四步，合并；经过以上三步变换后，进一步整理得到等效电路；再将电阻合并后得到一个新的三孔电路网络，从而达到了将四网孔简化成三个网孔的目的。

在本发明的上述技术方案中，所述lzs-dspl模型是一种通过考虑土壤纵向电阻的能够适用于埋地油气管道受地磁暴影响的分布源管道数学模型，用来计算确定土壤电场强度和管道电场强度，选择土壤纵向电阻的有效面积，计算管道gic和psp，进行误差判据。lzs-dspl模型的建模方法、计算公式、参数说明等，详细记载于本申请人在先提交的申请号为201510579331.x的发明专利申请文件中。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动性的前提下，还可以根据这些附图获得其他的附图。

图1为按照本发明的大规模埋地油气管道gic和psp计算方法的一优选实施例的计算方法过程示意图；

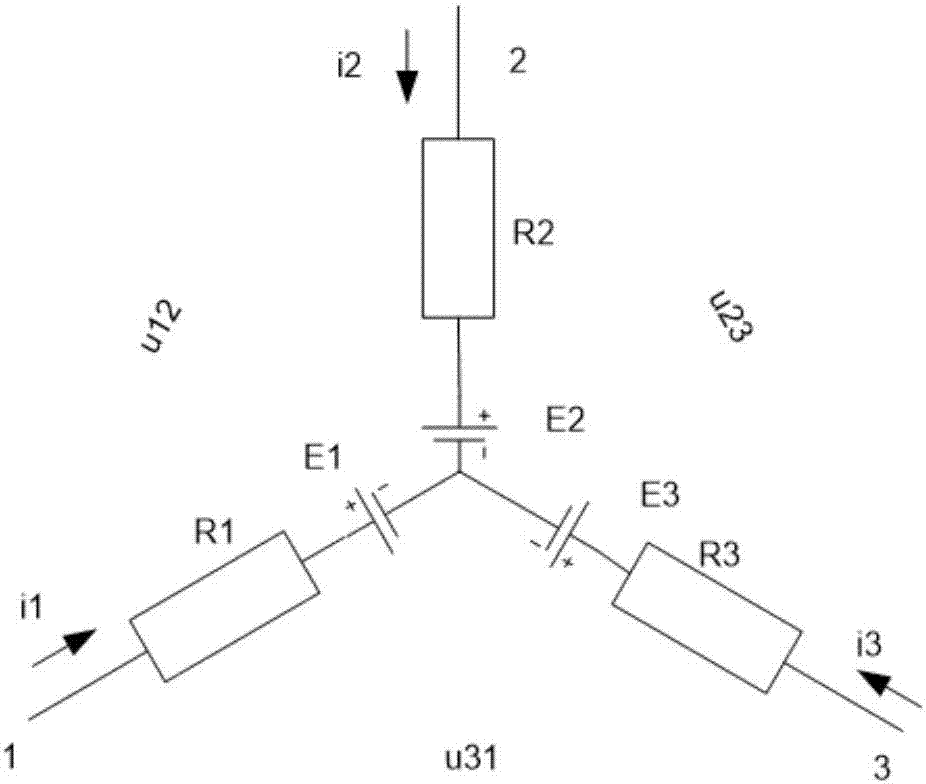
图2为按照本发明的大规模埋地油气管道gic和psp计算方法的一优选实施例的有源y型联结网络结构示意图；

图3为按照本发明的大规模埋地油气管道gic和psp计算方法的一优选实施例的有源△型联结电路结构示意图；

图4为按照本发明的大规模埋地油气管道gic和psp计算方法的一优选实施例的非对称y—△型联结电路有源变换示意图；

图5至图10为按照本发明的大规模埋地油气管道gic和psp计算方法的一优选实施例的电路网络的等效过程示意图；

图11为按照本发明的大规模埋地油气管道gic和psp计算方法的一优选实施例的大规模管道的原始等效电路结构示意图；

图12为按照本发明的大规模埋地油气管道gic和psp计算方法的一优选实施例的大规模管道的计算p1段管道gic和psp分布示意图；

图13为按照本发明的大规模埋地油气管道gic和psp计算方法的一优选实施例的大规模管道的计算p2段管道gic和psp分布示意图；

图14为按照本发明的大规模埋地油气管道gic和psp计算方法的一优选实施例的大规模管道的计算p3段管道gic和psp分布示意图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

为了解决现有技术中含非线性电路的大规模埋地油气管道gic和psp求解所存在的难题，本发明实施例提供了一种基于广义对称分量的直流有源电路等效的大规模埋地管道gic和psp计算方法。如图1所示，本实施例的思想方法为：第一步，将大规模埋地油气管道等效电路分成若干部分；第二步，选取大规模埋地油气管道等效电路的若干部分之一，保留其非线性电路部分，利用有源y—△型联结电路变换正变换和有源y—△型联结电路逆变换，对大规模埋地油气管道等效电路的其余部分进行等效电路变换实现简化，从而将高阶大规模埋地油气管道等效电路变成低阶埋地油气管道等效电路；第三步，利用回路电流方程或节点电压方程求解低阶埋地油气管道等效电路gic和psp；第四步，将大规模埋地油气管道等效电路的若干部分的每一部分都分别扫描计算一遍，集成若干部分的计算结果就会得到大规模埋地油气管道gic和psp全部结果。

大规模埋地油气管道gic和psp的回路电流和节点电压计算方法分别如下。

大规模埋地油气管道gic和psp的回路电流计算方法：

第一步骤，给定计算机及其算法所能计算的最多回路数(回路数是指使用回路电流法求解直流电路电流和电压所定义的回路数)，用符号mloop表示；

第二步骤，给出被研究管网对象和与其对应的整体等效电路(以下简称原电路)；

第三步骤，将电路中的非线性元件和关键节点部分电路定义保留标记，其回路数用符号kloop表示，很显然，除保留电路外，电路的其余部分均为线性电路；

第四步骤，将原电路进行划分得到n段原电路，在n段原电路中的每段原电路的回路数为lloop，其约束条件为：lloop+kloop＜mloop，算法能够求出正确解；

第五步骤，选取初值：i＝1；

第六步骤，提取第i段原电路；这里欲仿真计算该第i段埋地油气管道对应电路的gic和psp分布；

第七步骤，对j＝1、2、…i-1、i+1、…、n(其中j≠i)段原电路分别使用“一段埋地油气管道的等效变换方法”对之线性电路进行等效变换，将非线性元件和关键节点部分电路保留，可分别得到对应的n-1段等效电路；

第八步骤，将等效后的电路称为第i段等效电路；将第i段原电路及其相连接的等效后的电路统称为第i段电路“后等效电路”；

第九步骤，利用回路电流方法仿真计算第i段后等效电路的gic和psp分布，保存第i段原电路的gic和psp分布结果；

第十步骤，判断：

如果i＜n，则变量i递增i＝i+1，转第七步骤，继续计算；

如果i＝n，输出i＝1、2、3……n段原电路的gic和psp分布结果，就是被研究管网对象的gic和psp分布结果；

第十一步骤，结束计算。

大规模埋地油气管道gic和psp的节点电压计算方法如下。

第一步骤：给定计算机及其算法所能计算的最多节点数(定义节点数：指使用节点电压法求解直流电路电流和电压所定义的节点数)，用符号mnod表示；

第二步骤：给出被研究管网对象和与其对应的整体等效电路(以下简称原电路)；

第三步骤：将电路中的非线性元件和关键节点部分电路定义保留标记，节点数，用符号knod表示，很显然，除保留电路外，电路的其余部分均为线性电路；

第四步骤：将原电路进行划分得到n段原电路，在n段原电路中的每段原电路的节点数lnod，其约束条件为：lnod+knod＜mnod，算法能够求出正确解；

第五步骤：选取初值：i＝1；

第六步骤：提取第i段原电路。这里欲仿真计算该段埋地油气管道对应电路的gic和psp分布；

第七步骤：对j＝1、2、…i-1、i+1、…、n(其中j≠i)段原电路分别使用“一段埋地油气管道的等效变换方法”对之线性电路进行等效变换，将非线性元件和关键节点部分电路保留，可分别得到对应的n-1段等效电路；

第八步骤：将等效后的电路称为第i段等效电路；

第九步骤：利用节点电压方法仿真计算第i段等效电路的gic和psp分布，保存第i段原电路的gic和psp分布结果；

第十步骤：判断，

如果i＜n，则变量i递增i＝i+1，转第七步骤，继续计算；

如果i＝n，输出i＝1、2、3……n段原电路的gic和psp分布结果，就是被研究管网对象的gic和psp分布结果；

第十一步骤：结束计算。

在本实施例的大规模埋地管道gic和psp计算方法中，有源y—△型电路变换方法：

基本概念：

根据有源y型联结和有源△型联结的电源情况，这里给出以下基本概念的定义。

有源对称y型联结电路：指有源y型联结电路三电源代数和为零的联结电路。

有源非对称y型联结电路：指有源y型联结电路三电源代数和不为零的联结电路。

有源对称△型联结电路：指有源△型联结电路三电源代数和为零的联结电路。

有源非对称△型联结电路：指有源△型联结电路三电源代数和不为零的联结电路。

无源△型联结电路：指△型联结电路支路上只有电阻没有电源电路。

无源y型联结电路：指y型联结电路支路上只有电阻没有电源电路。

很显然，无源△型联结电路和无源y型联结电路没有对称和不对称之分。

研究表明，根据有源y—△型联结电路定义，在有源y—△型联结电路变换中，由对称y、不对称y、对称△和不对称△组合有8种，但只有以下4种是有用的。有源y→△型联结电路变换可以分成两种算法：有源对称y型联结电路→对称△型联结电路变换算法和有源不对称y型联结电路→对称△型联结电路变换算法，简称为有源y—△型联结电路正变换算法。有源对称△→y型联结电路变换可以分成两种算法：有源对称△→y型联结电路变换算法(简称有源y—△型联结电路逆变换算法a)、有源不对称△→y型联结电路变换算法(简称有源y—△型联结电路逆变换算法b)。而实际上，有源y—△型联结电路逆变换算法a是有源y—△型联结电路逆变换算法b的一种特殊情况，所以，可以将两种情况算法合并为统一的一种算法，即有源y—△型联结电路逆变换算法。以下分别给出如下变换算法的对应参数和公式推导过程和步骤。结合图2至3的有源电阻网络的等效图进行说明。

(1)有源y—△型联结电路正变换算法

有源y(对称或不对称y型)联结电路→对称△型联结电路变换被定义为有源y—△型联结电路正变换算法。同无源y—△型联结电路网络构造一样，有源y—△型联结电路变换网络，分别标注出相应端号，流经三个端点的电流为i1、i2和i3；端点间的电压为u12、u23和u31。

有源y型联结网络如图2所示，e1、e2和e3分别为y型联结支路上的电源电势，r1、r2和r3分别为y型联结支路上与电源电势相对应的的电阻(注：这里电阻参数为非实时变化参数)，并且按如该图规定正方向。按照基尔霍夫电压定律(kcl)和基尔霍夫电流定律(kvl)推导，有如下关系

由有源y型联结网络方程组解得电流值分别为i1、i2和i3：

对于如图3所示有源△型联结电路，标注出相应端点处的电流和端点间的电压，e12、e23和e31分别为△型联结电路支路上的电源电势，r12、r23和r31分别为△型联结电路支路上与电源电势相对应的电阻(注：这里电阻参数为非实时变化参数)，设该图中方向为参考方向，按照基尔霍夫电压定律(kcl)和基尔霍夫电流定律(kvl)推导得

根据等效变换条件，不论电压u12、u23和u31与电势e1、e2和e3为何值，如果两个电路等效的话，流入对应端子的电流应该相等，对应端子之间的电势应该相等。所以，由y型联结和△型电路联结网络得到的与电流对应的各项应分别相等，即：u12、u23和u31前的系数应该相等，于是可得y型－△型联结电路电阻和电势的等效变换公式分别为

由(5)式可以看出，由于e12、e23和e31之和为零，所以，无论是对称y型联结和非对称y型联结变换得到的△型联结电路均为对称△型联结电路，这里对称y型电路联结和非对称y型电路联结没必要加以区别。

(2)有源y—△型联结电路逆变换算法a

有源对称△型→y型联结电路变换被定义为有源y—△型联结电路逆变换算法a。根据如上的推导过程，当有源△型联结电路网络电势e12、e23和e31满足e12+e23+e31＝0时，就可以按照基尔霍夫定律进行对称△－y型联结电路变换，电阻变换公式如下

根据电势等效公式，由于电源代数和为零，(5)式将会线性相关，将会产生无数组解，因此，可以确定其中一个变换电源,例如，可以先设定e1的值,再求出其他两个电源值。由(5)式可得

(3)有源y—△型电路逆变换算法b。

有源非对称△→y型联结电路变换算法被定义为有源y—△型联结电路变换算法b。在实际应用中，等效模型往往出现非对称△型联结电路需要变换成y型联结电路网络的情况，当有源△型联结电路网络中三电势之和不为零时，电阻可以按照y－△型联结电路变换公式求得，但电源的等效将不满足条件，无法求得，此时，电源的等效需要借助广义直流对称分量法来进行分析换算。

这里，将不对称交流电力系统计算的对称分量法的概念引用到直流电路中。在直流电路中，直流电源的相位虽然有同相位和反相位之区别，但这里没有利用相位来严格定义其对称分量。而是利用正序和负序分量的核心本质(任意时刻代数和相加等于零)来定义直流电源的正序和负序分量。所以，将之称为广义直流对称分量法。相对应的直流电源的正序、负序和零序分量分别为：广义正序分量、广义负序分量和广义零序分量。

(a)对非对称△型联结电路的直流电源e12、e23和e31进行广义直流对称分量分解

对直流电源e12、e23和e31进行广义直流对称分量分解，有

其中，ea1、eb1和ec1为广义正序电压源分量，ea2、eb2和ec2为广义负序电压源分量，ea0、eb0和ec0为广义零序电源电压分量。

根据对称分量法，广义正序和广义负序电源电压分量的关系式为

对于△型联结电路而言，设广义零序电源电压分量ea0、eb0和ec0有如下关系

其中，ia0、ib0、ic0和i0分别为对应的广义零序电流源分量。

由(10)式可得

ea0+eb0+ec0＝i0*(r12+r23+r31)(11)

由(8)式各式相加，可得

ea0+eb0+ec0＝e12+e23+e31(12)

将(11)式代入(12)式，可得

i0＝(e12+e23+e31)/(r12+r23+r31)(13)

将(11)式代入(8)式，可得

任意设(14)式中两个变量分别为某数值，例如取ea1和eb1分别为不为零某数值，则可求得ea2和eb2的表达式为

将(15)式代入(9)式，可求得ec1和ec2

至此，在取定ea1和eb1分别为某数值后，利用(15)式和(16)式可求得广义正序电源电压分量(ea1、eb1和ec1)和广义负序电源电压分量(ea2、eb2和ec2)。利用(10)式和(13)可求得广义零序电源电压分量(ea0、eb0和ec0)。

(b)叠加原理

根据前面讨论，对非对称△型联结电路的e12、e23和e31进行广义直流对称分量分解，可得广义正序电源电压分量(ea1、eb1和ec1)、广义负序电源电压分量(ea2、eb2和ec2)和广义零序电源电压分量(ea0、eb0和ec0)。可利用叠加原理将广义各序电源电压分量变换合成，得到y型联结电路的电源电压。

其中，esa1、esb1和esc1为y型联结电路广义正序电源电压分量；esa2、esb2和esc2为y型联结电路广义负序电源电压分量；esa0、esb0和esc0为y型联结电路广义零序电源电压分量。

广义正序电源电压分量：在广义正序电源电压分量(ea1、eb1和ec1)的作用下，根据对称△—y型联结电路变换方法，可求广义正序电源电压分量esa1、esb1和esc1。

广义负序电源电压分量：在广义负序电源电压分量(ea2、eb2和ec2)的作用下，根据对称△型—y型联结电路变换方法，可求广义负序电源电压分量esa2、esb2和esc2。

广义零序电源电压分量：同交流电力系统的零序分量概念一样，由于广义零序电压分量施加在△型联结电路侧，无论另一侧接线方式如何，都没有广义零序电流流过(相当于零序电阻为无穷大)，所以，只有在y型联结等效电路里没有广义零序电压源，才能与△型联结电路等效，实现y型联结电路无广义零序电流分量。所以，必须忽略广义零序电源电压分量(ea0、eb0和ec0)的作用影响，

即：ea0＝0、eb0＝0ec0＝0(18)

实际上，由于使用广义零序电源电压分量(ea0、eb0和ec0)求解困难或无法求解，这里，利用了广义零序电压分量的特征，无需讨论或给出广义零序分量的解法，就能够巧妙地达到求解等效电路的目的，之后将给出实例论证。至此，将式(18)代入式(17)，可得y型联结电路的等效电源可取为

电阻变换公式如下

由上述论证可知，非对称y型联结有源网络的电源电势可以按照广义直流对称分量法分解为广义三相对称分量(正序、负序和零序电压分量)，在变换到y型联结有源网络过程中可以将之分解为正序源△型联结电路网络、负序源△型联结电路网络和零序源△型联结电路网络，电阻的的变换完全按照无源电阻y—△型联结电路变换规则即可，不受影响。对于正序、负序源△型联结电路网络来说，电势之和对称，根据y—对称△型联结电路有源网络变换方法可以等效成相应的y型联结源网络，而零序源△型联结电路网络非对称且对外端口不产生y型联结电势分量可将之忽略，最终可将变换后的y型联结源网络进行叠加，如图6所示，得到非对称△—y型联结电路有源网络的变换结果。

在本实施例的大规模埋地管道gic和psp计算方法中，一段埋地油气管道的等效变换方法：

选取埋地油气管道lzs-dspl模型中一段四孔网络，如图5所示，埋地油气管道参数r11、r12、r13和r14代表埋地油气管道纵向电阻，r21、r22、r23、r24和r25表示涂层横向电阻，r31、r32、r33和r34表示土壤纵向电阻，e11、e12、e13和e14表示埋地油气管道附近电场强度(注：这里电阻参数为非实时变化参数)。

简化网孔的具体过程如图5至图10所示。从左至右分别称为第一、第二、第三和第四网孔。这里的目的是将如图5所示的四网孔进行合并，简化成如图10所示的三个网孔。也就是说，将如图5所示的从左数第二和第三网孔进行合并，简化成如图10所示的第二个网孔。

具体的技术路线如下：

第一步，y→△型联结电路有源网络变换(有源y—△型联结电路正变换算法)。利用有源y型—对称△型联结电路联结变换(有源y—△型联结电路变换算法a)，y－△型联结电路有源网络变换就可以将如图5所示的从左数第二和第三网孔进行合并而简化电路。在图5中，r12、e12、r13、e13和r23三个支路组成一个y型联结网络，经过变换可以等效成一个新的△型联结电路网络，在图6中用虚线部分用r1、e1、r2、e2、r3、e3表示△型联结电路的三个支路，等效后如图7所示。可见，经过变换后，原来的四个网孔变成了5个网孔。

第二步，左△→y型联结电路有源网络变换(采用有源y—△型联结电路逆变换算法。如果△为有源对称△，则采用有源y—△型联结电路逆变换算法a；如果△为有源非对称△，则采用有源y—△型联结电路逆变换算法b)。在图8中，从左数第二个网孔r32、r22、r3、e3三个支路组成一个△型联结电路网络，经过△－y型联结电路变换可以等效成y型联结电路网络r1’、e1’、r2’、e2’、r3’、e3’三个支路。

第三步，右△→y型联结电路有源网络变换(采用有源y—△型联结电路逆变换算法。如果△为有源对称△，则采用有源y—△型联结电路逆变换算法a；如果△为有源非对称△，则采用有源y—△型联结电路逆变换算法b)。与第二步同理，在图8中，与之对称的从左数第4个网孔r33、r24、r2、e2三个支路也可以等效成一个y型联结网络r1″、e1″、r2″、e2″、r3″、e3″三个支路。

第四步，合并。经过以上三步变换后，进一步整理得到如图9所示的等效电路。再将电阻合并后得到一个新的三孔电路网络如图10所示，从而达到了将4网孔简化成3网孔的目的。

在具体实施中，采用本实施例的技术方案，进行大规模埋地油气管道gic和psp的回路电流计算：

对于图11至14所示的油气管道假定由p1、p2、p3、p4、p5、p6、p7等7段子管道构成，假定每一段子管道有10个等效回路，同时，假定每一段子管道有11个等效节点。加装b1和b2去耦合器进行油气管道保护。假设油气管道的b1和b2为具有非线性特性的去耦合器，当整个管道网络规模增大时求管道变量的解很困难。因此，计算的大前提是保留b1和b2两个支路。利用本发明实施例中提供的“大规模埋地油气管道gic和psp的回路电流计算方法”求解管道系统gic和psp，其具体步骤为：

第一步骤：给定计算机及其算法所能计算的最多回路数，假定mloop＝2000；

第二步骤：给出被研究管网对象和与其对应的整体等效电路如图11所示；

第三步骤：将电路中的非线性元件b1和b2的位置保留；为简单起见，假定保留回路数kloop＝0；

第四步骤：将原电路进行划分得到7段原电路，在7段原电路中的每段原电路的回路数为lloop＝10，满足约束条件为：kloop+lloop＜mloop＝2000，算法能够求出正确解；

第五步骤：选取初值：i＝p1

第六步骤：提取第i段原电路，并保留电路中的非线性元件b1和b2的位置；

第七步骤：对于j＝p2、p3、p4、p5、p6、p7等6段管道段原电路分别使用“一段埋地油气管道的等效变换方法”对之线性电路进行等效变换；由于非线性元件b1和b2的位置限制，而对于j＝p3段管道段原电路必须使用有源y型—△型联结电路变换方法，否则无解；

第八步骤：将第i段原电路及其相连接的等效后的电路称为第i段电路“后等效电路”；第j＝p1段后等效电路如图12所示、第j＝p2段后等效电路如图13所示、第j＝p3段后等效电路如图14所示、其余j＝p4、p5、p6、p7段后等效电路与此类推，不再赘述；第九步骤：利用回路电流方法仿真计算第i段后等效电路的gic和psp分布，保存第i段原电路的gic和psp分布结果；

第十步骤：判断，

如果i＜n，则变量i递增i＝i+1，转第七步骤，继续计算；

如果i＝n，则输出i＝1、2、3……n段原电路的gic和psp分布结果，就是被研究管网对象的gic和psp分布结果；

第十一步骤：结束计算。

在具体实施中，采用本实施例的技术方案，进行大规模埋地油气管道gic和psp的节点电压计算：

对于图11至14所示的油气管道假定由p1、p2、p3、p4、p5、p6、p7等7段子管道构成，假定每一段子管道有11个等效节点。加装b1和b2去耦合器进行油气管道保护。假设油气管道的b1和b2为具有非线性特性的去耦合器，当整个管道网络规模增大时系统节点数随之增大，求解管道变量很困难。因此，计算的大前提是保留b1和b2两个支路。利用本发明实施例中提供的“大规模埋地油气管道gic和psp的节点电压计算方法”求解管道系统gic和psp，其具体步骤为：

第一步骤：给定计算机及其算法所能计算的最节点数，假定mnod＝2000；

第二步骤：给出被研究管网对象和与其对应的整体等效电路如图11所示；

第三步骤：将电路中的非线性元件b1和b2的位置保留；为简单起见，假定保留节点数knod＝0；

第四步骤：将原电路进行划分得到7段原电路，在7段原电路中的每段原电路的节点数为lnod＝10，满足约束条件为：lnod+knod+0＜mnod＝2000，算法能够求出正确解；

第五步骤：选取初值：i＝p1

第六步骤：提取第i段原电路，并保留电路中的非线性元件b1和b2的位置；

第七步骤：对于j＝p2、p3、p4、p5、p6、p7等6段管道段原电路分别使用“一段埋地油气管道的等效变换方法”对之线性电路进行等效变换；由于非线性元件b1和b2的位置限制，而对于j＝p3段管道段原电路必须使用有源y型—△型联结电路变换方法，否则无解；

第八步骤：将第i段原电路及其相连接的等效后的电路称为第i段电路“后等效电路”；第j＝p1段后等效电路如图12所示、第j＝p2段后等效电路如图13所示、第j＝p3段后等效电路如图14所示、其余j＝p4、p5、p6、p7段后等效电路与此类推，不再赘述；这里符号p1、p2、p3、p4、p5、p6、p7表示原管道对应的等效电路，pe1、pe2、pe3、pe4、pe5、pe6、pe7表示与原管道对应的化简后等效电路；

第九步骤：利用节点电压方法仿真计算第i段后等效电路的gic和psp分布，保存第i段原电路的gic和psp分布结果；

第十步骤：判断，

如果i＜n，则变量i递增i＝i+1，转第七步骤，继续计算；

如果i＝n，则输出i＝1、2、3……n段原电路的gic和psp分布结果，就是被研究管网对象的gic和psp分布结果；

第十一步骤：结束计算。

以上所述仅是对本发明的优选实施方式进行描述，并非是对本发明的范围进行限定；以上所述仅为本发明的具体实施方式而已，并不用于限定本发明的保护范围；在不脱离本发明设计精神的前提下，本领域普通工程技术人员对本发明的技术方案作出的任何修改、等同替换、改进等，均应落入本发明的权利要求书确定的保护范围内。

本发明专利得到国家重点研发计划项目(no.2016yfc0800103)基金资助。