一种基于CBM的机队维修决策方法与流程

本发明涉及基于cbm的机队维修决策方法。

背景技术：

目前，飞机结构疲劳寿命的计算方法通常采用应力寿命和损伤容限分析方法(heyuting,duxu,zhangteng,etal.afewprimaryelementscontrollingaircraftstructuralservicelife[j].journalofairforceengineeringuniversity(naturalscienceedition),2017,18(3):1-8.[何宇廷，杜旭，张腾，崔荣洪.飞机结构寿命控制中的几个基本问题[j].空军工程大学学报(自然科学版),2017,18(3):1-8.])，出于对结构安全的考虑，得到的计算寿命值往往会除以一个安全寿命系数(一般取2)作为结构的设计寿命，当设计寿命值消耗殆尽时对结构进行强制维修或更换。而在实际的使用过程中，往往会出现已到设计寿命，结构却完好，飞机结构疲劳寿命并未消耗殆尽就被强制维修和更换的现象，造成装备资源利用率低，经济性变差(wangyw,goguc,binaudn,etal.acostdrivenpredictivemaintenancepolicyforstructuralairframemaintenance[j].中国航空学报(英文版),2017,30(3):1242-1257.)。随着飞机结构健康监控技术(baishengbao,xiaoyingchun,liumabao,etal.engineeringapplicabilityofmonitoringcrackbysmartcoatingssensor[j].nondestructivetesting,2015,37(1):42-44.[白生宝,肖迎春,刘马宝,等.智能涂层传感器监测裂纹的工程适用性[j].无损检测,2015,37(1):42-44.])(structuralhealthmonitoring，shm)的不断进步，充分利用传感器获得的结构实时状态信息通过疲劳寿命计算模型来准确评估结构疲劳状态，实现剩余寿命(remainingusefullife，rul)的精准预测已经成为飞机结构视情维修(condition-basedmaintenance，cbm)(ganjie,zengjiaochao,zhangxiaohong.maintenancedecisionmodelwithperformancereliabilityconstraint[j].computerintegratedmanufacturingsystems,2016,22(4):1079-1087.[甘婕，曾建潮，张晓红.考虑性能可靠度约束的维修决策模型[j].计算机集成制造系统,2016,22(4):1079-1087.]zhangm,yez,xiem.acondition-basedmaintenancestrategyforheterogeneouspopulations[j].computersandindustrialengineering,77(2014):103-114.)采用的手段，而如何构建准确的疲劳寿命计算模型成为其中的关键。由于传感器采集的信息存在噪声，结构材料强度存在分散性，载荷形式多样，工况环境复杂多变，建立考虑多种不确定性因素的结构疲劳寿命预测模型，获得精准的寿命预测结果，为合理制定飞机维修方案，确保飞行安全，降低维修成本成为重点解决的问题。

在飞机cbm方面，国内现有的大部分研究都是针对民用航空发动机和非结构件(如电子器件)。将飞机结构的寿命预测作为飞机维修决策的约束条件，从整个机队层面同时将机队的维修费用和保有率作为维修决策的优化目标，并充分考虑维修资源的承载能力的cbm研究成果还十分有限。

技术实现要素：

本发明的目的是为了解决现有方法是针对民用航空发动机和非结构件，单机保有率达不到训练要求，以及没有考虑机队的维修成本的缺点，而提出一种基于cbm的机队维修决策方法。

一种基于cbm的机队维修决策方法包括以下步骤：

步骤一：进行飞机疲劳结构的剩余寿命预测，得到疲劳结构的剩余寿命；

步骤二：根据步骤一得到的疲劳结构的剩余寿命，建立单机维修成本决策优化模型；

步骤三：根据步骤二建立的单机维修成本决策优化模型，建立机队的维修成本决策优化模型；

步骤四：建立机队保有率优化模型；

步骤五：根据步骤三和步骤四建立机队的多目标优化决策模型，根据多目标优化决策模型采用非支配排序的多目标优化算法(nsga-ii)方法确定机队各飞机疲劳结构的最优维修方案。

所述飞机疲劳结构为壁板、耳片、机翼的盒段、发动机的叶片、起落架等。

本发明的有益效果为：

为了避免材料、制造、状态信息不完备、工况噪声等不确定因素对结构疲劳寿命预测的影响，本发明提出了将扩展卡尔曼滤波(ekf)和实时状态数据相结合的结构剩余寿命(rul)预测方法，通过对结构的疲劳裂纹扩展模型中的不确定性参数进行实时更新，使模型具有自适应消除噪声能力，提高了寿命预测精度。以结构的rul预测结果和维修资源为约束，以机队维修费用和保有率为目标，建立了一个基于视情维修(cbm)的机队多目标维修决策优化模型。仿真结果表明，本发明具有较好的预测精度，维修决策优化模型在保证结构安全的前提下，实现了维修成本和机队保有率的最优化。

附图说明

图1为基于cbm的机队维修决策方法体系图；

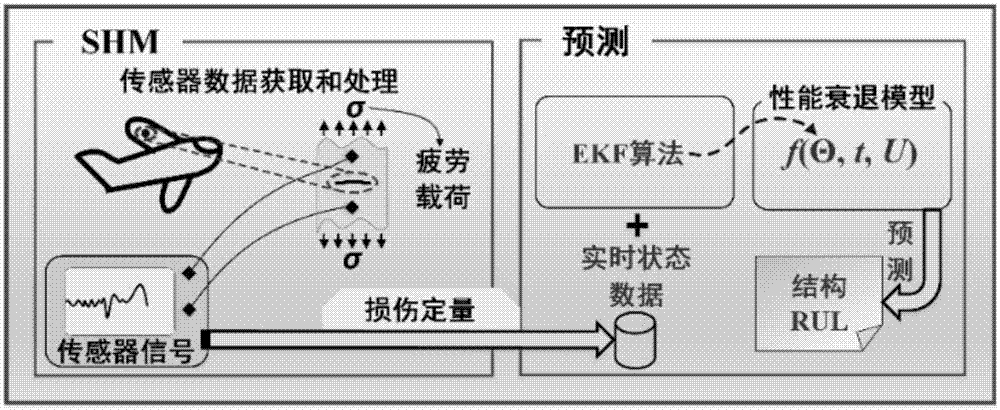
图2为基于ekf算法的疲劳裂纹rul预测框架；

图3为基于ekf算法的结构rul预测流程；

图4为结构剩余寿命浪费和结构不同损伤程度下的维修级别示意图；a为左侧图，为结构剩余寿命浪费；b为右侧图，结构不同损伤程度下的维修级别；

图5为10个试件的裂纹扩展曲线图；

图6为10个试件的疲劳性能参数拟合结果图；

图7为试件2的参数评估和寿命预测仿真结果图；

图8为试件4的参数评估和寿命预测仿真结果图；

图9为试件6的参数评估和寿命预测仿真结果图；

图10为试件8的参数评估和寿命预测仿真结果图；

图11为维修决策优化结果图；

图12为优化方案甘特图。

具体实施方式

具体实施方式一：一种基于cbm的机队维修决策方法包括以下步骤：

传统的cbm主要分为三个步骤：a.实时状态数据获取→b.rul预测(或故障诊断)→c.维修决策。依据cbm的维修理念，面向机队的维修决策方法体系如图1所示。

由图1可知，基于cbm的理念，方法体系以机队为管理对象，在机群同步协调的基础上，注重飞机多个部件的实时健康状态健康和分析，实现了飞机状态监控，rul预测(故障诊断)，维修决策，维修实施等过程的一体化集成。方法体系利用ekf算法，结合结构实时健康状态数据，对结构疲劳裂纹扩展模型中的不确定性参数进行实时更新，克服了传统疲劳裂纹扩展模型由于数据噪声影响而预测精度低的缺陷。在维修决策方面，方法体系以结构的rul预测结果和维修资源为约束，以机队维修费用和保有率为目标，建立了一个机队多目标维修决策优化模型，避免了传统维修决策模型优化目标单一的缺陷。

步骤一：进行飞机疲劳结构的剩余寿命预测，得到疲劳结构的剩余寿命；

步骤二：根据步骤一得到的疲劳结构的剩余寿命，建立单机维修成本决策优化模型；

步骤三：根据步骤二建立的单机维修成本决策优化模型，建立机队的维修成本决策优化模型；

步骤四：建立机队保有率优化模型；

步骤五：根据步骤三和步骤四建立机队的多目标优化决策模型，根据多目标优化决策模型采用非支配排序的多目标优化算法(nsga-ii)方法确定机队各飞机疲劳结构的最优维修方案。

具体实施方式二：本实施方式与具体实施方式一不同的是：所述步骤一中进行飞机疲劳结构的剩余寿命预测，得到疲劳结构的剩余寿命的具体过程为：

步骤一一：建立系统状态参数转移方程和观测方程；

系统状态参数转移方程为：

θk＝f(θk-1)+wk-1

其中θk为系统状态参数向量，wk-1系统噪声向量，k为时间或载荷周期；式中f(·)为系统状态转移方程，f＝[g(ak-1),ck-1,mk-1]^t；wk-1为系统噪声向量，wk-1＝[wa,k-1,wc,k-1,wm,k-1]^t，wa,k-1、wc,k-1、wm,k-1分别为ak、ck、mk的系统过程噪声，wc,k-1服从wc,k-1～n(0,qc,k-1)，qc,k-1为wc,k-1的方差，wm,k-1服从wm,k-1～n(0,qm,k-1)，qc,k-1为wc,k-1的方差，，qc,k-1和qm,k-1分别由材料的疲劳试验确定，wa,k-1为系统过程噪声，且服从wa,k-1～n(0,qa,k)，qa,k为wa,k-1的方差；

系统状态参数观测方程为：

zk＝h(θk)+vk

其中zk是观测值，h表示测量函数，在中为恒等函数；vk表示测量误差，且其服从vk～n(0,rk)；所述系统状态参数为疲劳结构裂纹和材料性能参数；

由于方程中状态参数a，c和m存在分散性，因此需要对其进行滤波，以提高寿命的预测精度。

步骤一二：对步骤一一建立的系统状态参数转移方程和观测方程利用扩展卡尔曼滤波算法进行滤波，得到准确的状态参数向量θk；

步骤一三：利用步骤一二得到的准确的状态参数向量θk，进行疲劳结构的裂纹扩展剩余寿命预测。

ekf算法的基本思想就是对非线性状态参数模型进行近似线性化，即将非线性模型围绕其滤波估计值和预测值作泰勒展开，通过忽略二阶以上的高阶项，得到局部线性化的状态参数模型，再应用传统的线性卡尔曼滤波算法实现递推估计。

对式(5)和(6)所示的离散状态转移方程和观测方程进行一阶泰勒展开，可得：

其中：

式中：fn和zn(n＝1，2，3)分别表示f和z的第n个分量(如f1＝g(ak))；f和h分别表示状态转移方程和观测方程的一阶微分矩阵，即线性雅克(jacobian)比矩阵。

假设通过shm技术获得了结构的前l步实时状态参数观测值，即z＝{z1,z2,…,zl}，则基于ekf算法的结构rul预测流程如图3所示。

由图3可知，整个预测流程分为参数评估和寿命预测两个部分。在参数评估部分，ekf算法利用实时状态参数观测值，对疲劳裂纹扩展模型中的状态参数进行不断的更新，以更好的反映结构裂纹的扩展趋势。在寿命预测部分，基于更新后的疲劳裂纹扩展模型，通过不断的迭代来求得结构的rul。

其它步骤及参数与具体实施方式一相同。

具体实施方式三：本实施方式与具体实施方式一或二不同的是：所述步骤一一中建立系统状态参数转移方程的具体过程为：

机械结构rul预测方法主要包括基于物理模型的方法和基于数据驱动的方法。基于物理模型的方法由于利用设备特定的物理学模型(性能衰退模型)，具有能够深入对象系统本质的性质，针对特定的设备可以实现较精确的rul预测(xiatangbin.researchondynamicprocessandpredictivemaintenanceschedulingforhealthmanagementofmanufacturingsystems[d].shanghai:shanghaijiaotonguniversity,2014,10-12.)，但在实际运用中，针对不同复杂系统建立精确的物理模型往往非常困难，且模型中的参数由于工况等因素的影响带有很大的不确定性。基于数据驱动的方法主要基于统计学理论和机器学习理论进行rul预测，其不需要建立确定的物理模型，但预测精度受训练数据限制，当训练数据不足时预测精度较低，且随着预测步数的增大预测精度往往下降较大(liuj,wangw,maf,etal.adata-model-fusionprognosticframeworkfordynamicsystemstateforecasting[j].engineeringapplicationsofartificialintelligence,2012,25(4):814-823.)。ekf算法作为基于数据驱动方法中的一种，由于能够充分利用实时状态数据对设备健康状态衰退模型中的不确定性参数进行估计，消除各种不确定性因素对rul预测精度的影响，被广泛的应用于设备rul的预测(chowdharyg,jategaonkarr.aerodynamicparameterestimationfromflightdataapplyingextendedandunscentedkalmanfilter[j].aerospacescience&technology,2010,14(2):106-117.)。但在将ekf算法和飞机结构的裂纹扩展模型相结合，提高rul预测精度的研究上还有待验证。图2为建立的基于ekf算法的疲劳裂纹rul预测框架。

图2中，采用f＝(θ,t,u)表示结构的性能衰退模型，其中：θ是影响结构性能衰退趋势的状态参数，受工况噪声及检测误差等因素影响通常带有不确定性；t表示载荷循环周期或者时间；u是给定参数，通常用来描述系统噪声，即工况、载荷等因素造成的噪声。由图2所示的疲劳裂纹rul预测框架可知，基于ekf算法，结合传感器获得的实时状态数据，对性能衰退模型f中带有不确定性的状态参数θ进行估计和实时更新，以消除系统噪声u对f模型预测精度的影响。

通过对不同种类的军用飞机进行机身结构疲劳试验，molentl等[4]得出了paris疲劳裂纹扩展公式能够充分处理飞机典型结构的疲劳裂纹扩展问题。因此，选取paris疲劳裂纹扩展公式来建立结构的疲劳性能状态参数评估模型。传统的paris公式如下：

式中a表示裂纹长度，n表示应力循环次数，da/dn表示裂纹扩展速率，c和m是材料系数，即疲劳性能参数；δk表示应力强度因子幅，δk与飞行过程中的常幅值载荷δσ和a，存在如下关系：

式中y为裂纹几何修正系数，与裂纹形式和大小相关；

由式(1)可知，裂纹扩展是一个连续的累积过程。通过欧拉(euler)方法，式(1)转换为如下的离散递归形式：

式中dt表示传感器采集状态信息的载荷间隔或时间间隔，由于飞行过程中受工况、载荷、气流以及压差等不确定因素的影响，疲劳结构疲劳裂纹的扩展过程难免存在噪声，则加入系统噪声后，式(3)表示如下：

ak＝g(ak-1)+wa,k-1(4)

式中g(·)为裂纹扩展方程，wa,k-1为系统噪声(即图2中的u)，且服从wa,k-1～n(0,qa,k)，qa,k为系统噪声方差，由决策者根据飞机的实际工作环境给出；

由式(3)可知，疲劳性能参数c和m的分散性，会造成裂纹长度呈现出一定的分散性。因此将裂纹长度a作为另一个需要评估的状态参数，则待评估的状态参数向量表示为θ＝[acm]^t，式(4)转换为系统状态参数转移方程。

其它步骤及参数与具体实施方式一或二相同。

具体实施方式四：本实施方式与具体实施方式一至三之一不同的是：所述步骤一三中利用步骤一二得到的准确的状态参数向量θk，进行疲劳结构的裂纹扩展剩余寿命预测的具体过程为：

利用步骤一二得到的准确的状态参数向量θk＝[ak,ck,mk]^t(第k步对应时刻的疲劳性能参数的评估值xk＝[ak,ck,mk]^t)，根据式(3)建立的疲劳裂纹扩展离散递归模型，得到k+l时刻的疲劳裂纹长度ak+l，l为裂纹长度扩展到大于临界裂纹的最小剩余步骤对应的时刻，l＞0；

满足式(6)的最小l定义为k时刻预测的疲劳裂纹rul：

ak+l≥ac(6)

式中ac表示疲劳结构临界裂纹长度。

其它步骤及参数与具体实施方式一至三之一相同。

具体实施方式五：本实施方式与具体实施方式一至四之一不同的是：所述步骤二中根据步骤一得到的疲劳结构的剩余寿命，建立单机维修成本决策优化模型具体为：

步骤二一：机队维修信息定义；

飞机作为一个复杂的机电液系统，由于设计和装配的复杂性，并非所有关键结构都能通过安装传感器来实时的进行健康状态的连续监控，因此只有部分运用了shm技术的关键结构(如机翼和机尾)可以采用cbm的理念，而另外缺少健康监测的关键结构(如发动机内部的核心单元体)仍然需要进行定期的检测和维修。由于执行定期维修计划的关键结构的维修费用是固定的，因此主要针对应用shm技术的关键结构进行维修决策方法研究。问题描述如下：

a、设一个机队共有z架飞机，每架飞机共有n个疲劳结构运用了疲劳结构健康监测(shm)技术；任意一个关键疲劳结构出现故障，飞机失效。关键疲劳结构的可靠性要求失效率小于10^-7；

b、基地共有k个维修机库为机队提供维修服务，k<z，且同一时刻一个维修机库只能为一架飞机提供维修服务，疲劳结构备件供应充足；

c、不同的疲劳结构能在同一次停机时进行维修；疲劳结构的维修费用由维修级别决定，不同飞机的相同疲劳结构在相同维修级别下的维修费用相同；维修级别分为两级：预防性维修和修复性维修；疲劳结构除更换以外，其它的维修方式都不能使疲劳结构恢复如新，并认为经历第i次维护活动以后，依据nakagawa[5]提出的故障率递增因子概念，疲劳结构的裂纹扩展模型将变为：λi+1(t)＝biλi(t)，其中bi为损伤率递增因子，λi(t)为通过第2节ukf算法和实时状态数据获得的疲劳结构疲劳裂纹扩展离散递归模型；

d、针对缺少健康监测的疲劳结构的定期维修时间间隔为t；

模型参数的定义见表1。

表1基于cbm的机队维修决策模型参数定义

关键结构为疲劳结构。

步骤二二：进行疲劳结构剩余寿命浪费成本计算：

出于对飞机安全的考虑，在以往的维修实践中，往往一发现故障征兆，立即对疲劳结构进行维修或者更换，这不但会使得疲劳结构的有效寿命不能充分利用，而且会造成大量的维修资源浪费。如图4中a图所示，飞机i已累计飞行t0小时(或循环载荷)，i＝1,2，…，m；如果飞机在ti,j时刻停机进入机库对疲劳结构j进行维修，则造成剩余寿命浪费，j＝1,2，…，n；ti,j为有效寿命时刻，飞机i疲劳结构j的剩余寿命(rul)浪费成本模型如下：

cost_ruli,j(ti,j)＝wj(tdesign-ti,j)(10)

式中tdesign为疲劳结构j疲劳裂纹达到临界裂纹ac时对应的飞行时间或循环载荷数，即为疲劳结构的设计服役寿命；cost_ruli,j(ti,j)为飞机i疲劳结构j在ti,j时刻进行维修的剩余寿命浪费成本；wj为第j个疲劳结构单位剩余寿命浪费成本；ti,j为飞机i的疲劳结构j的维修时刻(时间)；

步骤二三：进行疲劳结构排除故障成本计算；

结构的损伤程度(裂纹长度)决定了维修级别，不同的维修级别需要不同的维修费用。如图4中b图所示，当结构的裂纹长度小于a1时，结构出现损伤，但失效概率较小，利用疲劳结构健康监测技术对疲劳结构的实时健康状态进行继续监测；当裂纹长度扩展到区间[a1,a2]时，结构的失效率接近设定的结构最大失效率(潜在故障状态)，此时可以通过预防性维修方法(如打止裂孔或者补丁)对结构进行排故；当裂纹长度大于a2时，结构处于功能故障状态，此时只能通过修复性维修方法(如大修或者更换)对结构进行排故；飞机i疲劳结构j的排除故障成本模型如下：

式中a1和a2由结构维修性和维修经验确定；gi,j(ti,j)为疲劳结构在ti,j时刻的裂纹长度，由式(3)结合扩展卡尔曼滤波算法获得的实时状态参数，通过递归得到；cost_repairi,j(ti,j)为飞机i疲劳结构j的排除故障成本；

步骤二四：进行停机成本计算；

对于单架飞机来说，由实时状态数据得到的各结构维修时间不尽相同，有些甚至差距很大，如果按照这些维修间隔来执行维修活动，飞机就需要不断地停机来对不同的结构进行维修，造成维修经济性变差；且由于不同结构间存在经济相关性，即结构每次维修时，除了需要考虑自身维修活动的费用，还需要考虑因拆卸、场地布置等维修资源筹备所需的费用，这部分费用与具体的结构类型无关，但如果多个结构同时维修，则可以共享维修资源，可以分摊维修活动费用，更可以节省停机成本。因此利用成组维修技术，从全局的角度出发，对飞机多个结构维修时机进行决策调整，在某一时间点将不同结构的维修任务集中起来一起执行，如果结构的维修时间与定期维修计划时间点重合，则可以大大降低因为停机维修造成的损失。飞机i疲劳结构j的停机维修成本模型表示如下：

cost_resuourcei,j(ti,j)＝α(ti,j)dc+ei,j+α(ti,j)si,j/ns(ti,j)(12)

式中cost_resuourcei,j(ti,j)为飞机i疲劳结构j的停机维修成本，α(ti,j)为停机时间重合系数，α(ti,j)＝0或1，当ti,j与定期维修计划时间点重合则α(ti,j)＝0，否则α(ti,j)＝1；ei,j表示疲劳结构j的不可分摊停机维修费用；si,j表示结构j的可分摊停机维修费用；ns(ti,j)表示ti,j时刻多个疲劳结构进行组合维修的结构数量；dc为单次停机时降低飞机可用度带来的成本；

步骤二五：根据步骤二一至步骤二四建立单机维修成本决策优化模型；

结构的维修成本由结构rul浪费成本，排故成本和停机成本组成。针对飞机i的n个疲劳结构以维修成本最小为优化目标的优化模型表示如下：

式中gi,j(·)为飞机i疲劳结构j的裂纹扩展方程，acj为第j个疲劳结构的临界裂纹，pofi,j(t)为飞机i第j个疲劳结构在t时刻的失效率，pa为单机允许的最大失效率，xi＝{ti,1,ti,2,...,ti,n}是模型的n维决策向量；tm表示飞机停机对结构进行维修的所有时间段；t|t∈tp,且表示飞机执行任务的所有时间段；tp为距离飞机下次翻修的时间间隔，dj为第j个关键结构维修所需时间，pai(t)表示飞机i在t时刻由n个结构串联时的单机失效概率；φ(ti,1,ti,2,...,ti,n)表示n个结构的停机维修次数，且其不能大于允许的最大停机次数max_down；cost_aircrafti表示飞机i所有结构的维修成本总和。

其它步骤及参数与具体实施方式一至四之一相同。

具体实施方式六：本实施方式与具体实施方式一至五之一不同的是：所述步骤三中根据步骤二建立的单机维修成本决策优化模型，建立机队的维修成本决策优化模型具体为：

其它步骤及参数与具体实施方式一至五之一相同。

具体实施方式七：本实施方式与具体实施方式一至六之一不同的是：所述步骤四中建立机队保有率优化模型具体为：

其中tl,o为飞机l的疲劳结构o的维修时刻(时间)；k为维修时刻，min_avail为机队要求需要处于战备状态的最少飞机数量，δ(ti,j+k,tl,o)维修时间重合系数，用来判断飞机i结构j的维修时间是否与飞机l结构o的维修时间重合，如果重合则取1，否则取0；down_aircraft(t)表示在t时刻处于维修状态的飞机数，down_aircraft(t)≥min_avail,t∈tp表示在维修决策期间内，任意时刻处于完好状态的飞机数量应该大于机队的最低战备需求；down_aircraft(t)≤k表示维修决策期间内，同一时刻停机维修的飞机数不能大于基地的维修机库数，避免给维修资源造成负担以及最大程度的提高飞机可用度；t∈tp表示机队在任意时刻，处于战备状态中失效率最小的min_avail架飞机，在执行任务时的失效率应该小于机队允许的最大风险。

其它步骤及参数与具体实施方式一至六之一相同。

具体实施方式八：本实施方式与具体实施方式一至七之一不同的是：述步骤五中根据步骤三和步骤四建立机队的多目标优化决策模型具体为：

与单机维修决策优化不同，机队维修决策优化需要考虑的因素更多，机队维修计划的制定不仅要优化单机的维修成本，保障单机的结构安全，而且要从长远的角度规划每架飞机的维修任务和维修资源的调度，满足机队的战备需求。基于cbm的机队维修决策依据各飞机结构的实时状态信息和分析得到的rul，综合诸多保障要素，以机队维修费用和保有率为目标，以维修资源为约束，建立一个面向机队的多结构维修决策模型。依据机队中各飞机的维修时间重合度越小，则处于战备状态的飞机越多，机队保有率越高，因此以机队在维修决策期间内的维修时间重合度模型作为机队的保有率优化模型。基于cbm的机队维修决策优化模型如下：

其它步骤及参数与具体实施方式一至七之一相同。

实施例一：

(a)rul寿命预测方法验证

利用文献(wuwf,nicc.statisticalaspectsofsomefatiguecrackgrowthdata.engineeringfracturemechanics,2007,74:2952-2963.)中的疲劳试验数据来进行验证分析，这些数据是一个飞机结构疲劳性能研究的试验成果。试验材料为在飞机制造上被广泛使用的2024-t351铝合金。选取wu中ca2组的10个试件进行分析。试验载荷为正弦载荷，峰值载荷为6.118kn，谷值载荷为3.882kn，应力比为0.63，试验结果如图5和图6所示。

由图5和图6可知，即使在相同的试验环境下，由于结构材料强度，载荷等因素的不确定性，导致10个试件的疲劳裂纹扩展趋势表现出分散性。

对式(1)两边取对数，可得

显然，log(da/dn)和logδk之间呈线性关系。通过将10个试件的a～n曲线采用7点递增多项式法进行数据处理，并运用最小二乘法进行线性拟合，可求得式(16)中的疲劳性能参数c和m。图6为疲劳性能参数拟合结果。现有的大量试验数据统计研究发现(molentl,bartersa.acomparisonofcrackgrowthbehaviourinseveralfull-scaleairframefatiguetests[j].internationaljournaloffatigue,2007,29(6):1090-1099.)，logc和m服从正态分布，通过对10个试样的数据进行统计分析，可以得到logc～n(-14.6072,0.4015²)和m～n(2.400,0.182²)。

用于寿命预测仿真实验的参数设置如表2所示。依据对疲劳性能参数的统计分析，分别选取3个状态参数的分布均值作为其初始状态。

表2仿真实验参数设置

基于表2的实验参数设置，选取4个试件(试件2、4、6和8)的前150000个载荷循环的疲劳裂纹数据作为获得的健康监测状态数据，利用ekf算法对状态参数c，m和a进行估计，根据估计得到的状态参数结果并对未来的150000个载荷循环下的结构裂纹长度进行预测。为了更好的分析和对比三种滤波算法在处理问题上的收敛性和优越性，使得到的仿真结果更可信，选择10个试件中的2、4、6和8号试件分别进行了50次仿真。如图4所示，为4个试件的参数评估结果。

分别利用50次的相对误差来评估ekf算法在参数评估和寿命预测上的表现。均值和绝对相对误差的计算如式(17)。

式中：ak表示在第k个载荷循环时试件的真实裂纹长度。为在第k个载荷循环时，50次仿真实验获得的均值。arek为在第k个载荷循环时，50次仿真结果的绝对相对误差。

表3为4个试件在4组不同载荷循环下(k＝60000，90000，120000，150000)得到的和arek。

表3试件1和2的4个评估参数计算结果

由图4和表4可知，ekf算法在参数评估阶段有着很好的稳定性，且相对误差都小于1％。在无滤波的情况下，受数据噪声影响，结构疲劳裂纹扩展模型的参数评估结果带有很大的波动性，且相对误差随着载荷循环数的增加越变越大。以上分析结果表明，ekf算法通过对结构的疲劳裂纹扩展模型(健康状态衰退模型)中的不确定性参数进行实时更新，可以避免各种不确定因素对参数评估的影响。

根据图5和图6中的结构rul预测流程，对4个试件的剩余寿命进行了50次仿真预测，结果如图7—图10和表4所示。

表44个试件的剩余寿命预测结果

由表4可知，ekf算法在4个试件上的相对误差都小于5％。由此可见，通过将ekf算法和结构的疲劳裂纹扩展模型相结合，可以避免各种不确定因素对rul预测的影响，提高寿命预测精度。

(b)机队维修决策优化模型验证

以一个机队包含10架飞机为例，每架飞机有6个关键结构(a、b、c、d、e和f)应用了shm技术。各关键结构的rul由提出的寿命预测模型结合实时状态数据获得，机队所有关键结构的rul信息如表5所示。

表5机队所有关键结构的rul信息

结构的维修级别，维修费用，维修时间，临界裂纹长度等信息如表6所示。

表6结构维修信息

单次停机成本dc＝8000元，单机失效率最低要求pa＝10^-5，机队执行任务允许的最大风险pf＝10^-4，距离飞机下次翻修的时间间隔tp＝800h，翻修期内允许的最大停机数max_down＝3，最低机队保有率要求min_avail＝70％，缺少健康监测的关键结构的定期维修时间间隔为350h，飞机每天执行任务的时间大约为6h。基于以上信息，采用nsga-ii(debk,pratapa,agarwals,etal.afastandelitistmulti-objectivegeneticalgorithm:nsga-ii[j].ieeetransactionsonevolutionarycomputation2002；6(2):182-197.)算法对建立的机队维修决策优化模型进行了优化，结果如图11所示。为了更好的理解得到的优化结果，其中一个优化方案以甘特图形式展示在图12中。

由图11可知，由于机队维修决策优化模型中的两个目标：维修成本和机队保有率，之间存在冲突，因此优化结果为一系列的非劣解。由图12可知，得到的优化方案满足机队最小保有率要求(70％)，为了充分减少停机带来的成本，飞机1，2和8会在定期维修时间(针对缺少健康监测的关键结构)进行维修。

本发明还可有其它多种实施例，在不背离本发明精神及其实质的情况下，本领域技术人员当可根据本发明作出各种相应的改变和变形，但这些相应的改变和变形都应属于本发明所附的权利要求的保护范围。