一种基于多故障机理耦合的机械结构可靠性分析方法与流程

本发明提供一种针对具有多故障机理耦合作用的机械结构进行可靠性分析的方法，属于机械设计、结构可靠性设计领域。

背景技术：

机械结构的故障多属于耗损型故障，损伤则是用于描述结构或材料在载荷的作用下性能退化并导致破坏的物理过程。工程上许多结构件，如一些飞机构件，一般都以疲劳损伤为主。以发动机涡轮盘为例，发动机启动后连续工作数小时，然后停车若干小时，再下一次启动，为一次载荷循环。但是，涡盘工作环境温度较高，伴随发生蠕变。因此当研究它们的寿命时，既要考虑疲劳的破坏作用，又要考虑蠕变及其与疲劳的耦合效应。又如铁路机车轮轨，其损伤归因于两个方面的机理：疲劳裂纹与磨损。由于轮轨滚动接触疲劳与磨损是不可分离的两种损伤形式，因此它们之间存在有一定的相互作用关系。轮轨损伤过程中，疲劳裂纹与磨损是相互作用的。在某些工况和某个损伤阶段，其中一种损伤机理起着关键作用，而另一种损伤机理可能被忽略掉。在另一个损伤阶段或某些工况下，这两种破坏机理对轮轨的寿命同等重要或它们的耦合行为起到关键决定作用。放松或加重一个方面的破坏机理会直接影响到另一个机理的破坏过程，例如，用油润滑接触表面，起到了一定的减磨作用，但又进入表面裂纹又加速了裂纹的扩展速率。此外，疲劳裂纹萌生与磨损之间也是相互作用的，例如，严重的磨损表面上带有脱落的碎片，这些碎片直接影响小裂纹的形成与发展，因为严重磨损能够消除表面上的小裂纹。综合来看，这类结构的损伤亦是一个累积的过程，但不是单一故障机理的作用，而是多故障机理的耦合作用，当总的损伤量达到材料所允许的临界损伤量时，故障便随之出现了。

目前，对于结构单一故障机理的可靠性分析，在机械行业已经开展了相对多的研究工作，对多故障机理的可靠性研究尚处于起步阶段。针对“一果多因”的常见故障，如何考虑“多因”之间的耦合性，建立损伤耦合模型，从而实现定量的描述多故障机理的累积效应是关键；如何建立多故障机理的可靠性模型、可靠寿命预测模型，从而形成对多故障机理耦合作用下的可靠性设计分析技术是亟待解决的问题。因此本发明考虑多种故障机理之间的耦合作用，利用损伤等效、贝叶斯更新等理论，提出一种结构可靠性设计、分析方法，以解决结构在复杂、多种机理作用下的失效预测问题。

技术实现要素：

本发明的目的是提供一种适用于结构发生多故障机理耦合失效的可靠性分析方法。通过可靠性分析，能够确定结构寿命、可靠度及其对因素的灵敏度。以两种机理为例，说明本方法的5个主要步骤：

1确定损伤等效主参量。选取各个故障机理的共有主参量，如应变、能量、损伤量等，以损伤等效为基本原则，借助多故障机理交互作用的力学机理分析，将多故障机理的作用影响使用同一参量表示，该参量即为损伤等效主参量。

2损伤等效物理模型构建。结合仿真和试验数据，用该主参量来表征两者交互作用对故障的贡献，从而可以线性叠加、非线性叠加的方式，将各单一机理的损伤，以及两故障机理交互作用的损伤，叠加获得总损伤，建立多机理的故障物理模型；或者按影响最终故障的主次，分为主要机理和次要机理，在主要机理模型中，将次要机理及其交互作用的影响通过修正系数的方式考虑进去，从而建立多机理的修正系数模型。

3参数化仿真。在利用cae工具进行机械应力、应变等响应的仿真基础上，由结构主要影响因素确定参数，通过调整参数控制结构几何形状、材料属性、载荷等，自动实现损伤等效物理模型的重构，以便于多次仿真，进行随机性分析。

4故障物理模型随机性分析。利用损伤等效物理模型和参数化仿真，考虑材料参数、载荷、结构尺寸等参数的随机性，借助抽样法、改进的一次可靠度方法等，分析结构可靠度、可靠性灵敏度、可靠寿命等。

5基于贝叶斯的模型随机性修正。充分利用产品研制、使用过程的数据，基于贝叶斯更新方法，修正故障物理模型随机性结果，提高分析精度。

本发明的特点是：能够考虑多个故障机理同时作用，以及交互作用，分析结构的可靠度、灵敏度，方法可行，具有较强的实用价值。

附图说明

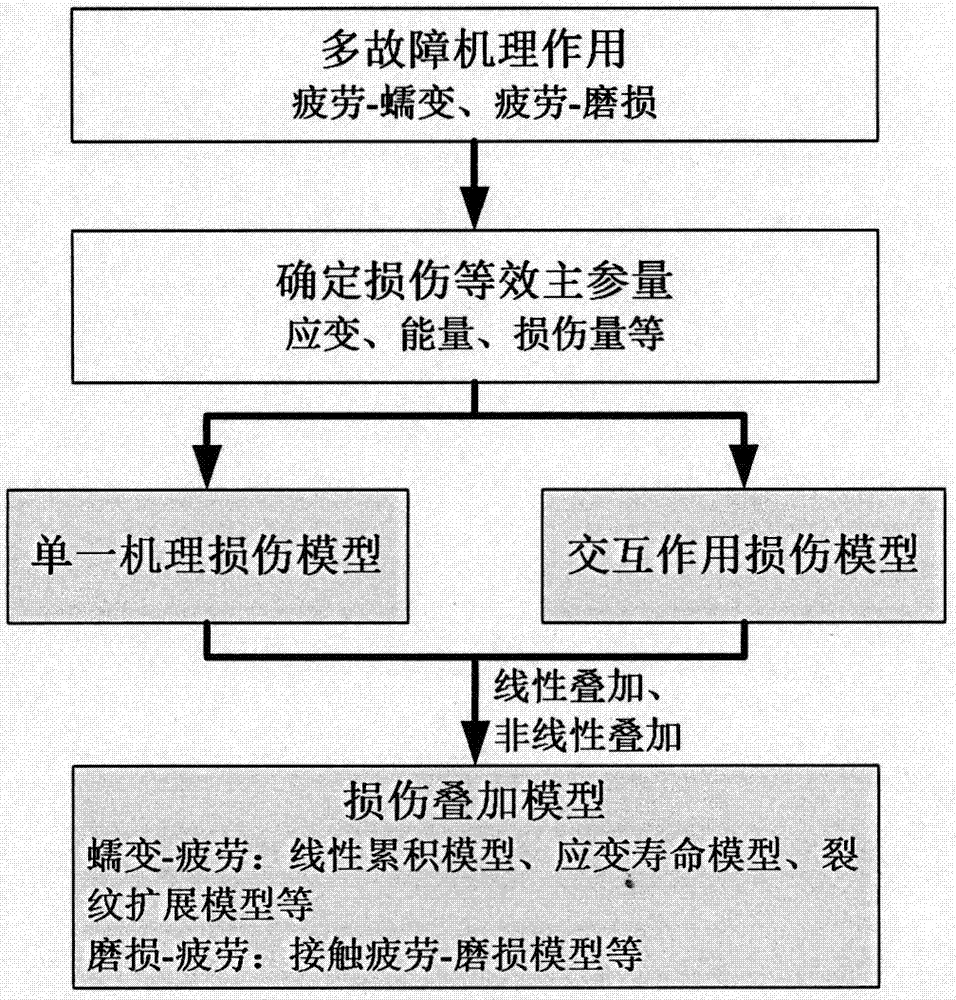
图1：本发明的流程图。

图2：损伤叠加模型构建流程

图3：修正系数模型构建流程

图4：基于贝叶斯的模型随机性修正流程

具体实施方式

本发明的流程图如图1所示，包括以下步骤：

1确定损伤等效主参量

工程上，机械结构疲劳、蠕变、磨损等故障机理模型较多，如疲劳故障机理的损伤模型主参量有损伤量、应变、应变能等，蠕变故障机理的损伤模型主参量有损伤量、应变、应变率、应变能等，磨损故障机理的损伤模型主参量有磨损量、磨损率、损伤量等。因此，当判断结构的所有故障机理，借助经验或实验，选取对应的故障物理模型。选取模型时，应该考虑两种故障机理的主参量一致，将有助于后续的交互作用计算和损伤等效。

2损伤等效物理模型构建

基于单一机理的物理模型以及损伤等效原理，根据多机理对结构故障的影响比重情况，分别构建以下两类模型。第一类，当各机理对故障的影响相差不大时，建立损伤叠加模型。另一类，当一种机理占主要，另一种机理次要时，如疲劳作用占主要，蠕变作用次要，构建修正系数模型，修正系数模型适合于蠕变较小(或温度不高)的场合，以简便、近似的方式处理工程问题。

1)损伤叠加模型

对于蠕变-疲劳、磨损-疲劳等多故障机理，在单一机理作用的物理模型的基础上，研究选择共有的主参量作为损伤等效量，如从故障表征参数选取共同物理量，并用该主参量来表征两者交互作用对故障的贡献，从而可以以线性叠加、非线性叠加的方式，将各单一机理的损伤，以及两故障机理交互作用的损伤，叠加获得总损伤，以便构建适应于多故障机理问题的损伤叠加模型，流程如图2所示。如对蠕变-疲劳故障机理能够建立线性累积模型、应变寿命模型、应变能模型、损伤力学模型、裂纹扩展模型等。

2)修正系数模型

针对工程中存在这么一类问题，结构在多故障机理作用，其中一种故障机理占主要，但另一种故障机理的作用不可忽略。如发动机气缸盖、活塞等结构，其工作温度为200～350℃，超过铝合金材料熔点的0.4，按照高温蠕变原理，其蠕变已达到发生条件，而且根据工程计算，只考虑疲劳的结果精度不高，故蠕变的影响不可忽略；但由于发动机的工作时间不长，如台架考核为700小时，相对于蠕变，疲劳作用更大。考虑到实际工程中蠕变模型的应用有一定局限性，如蠕变试验周期长、材料蠕变参数难以获取等问题。

对于这一类问题，可在成熟的疲劳模型基础上，借助力学机理、cae仿真、试验等手段，分析蠕变对结构的损伤及交互作用对结构的损伤，利用损伤等效的原理，将蠕变的影响通过修正系数的方式考虑进去，从而可利用修正后的疲劳模型预计蠕变-疲劳寿命，即获得蠕变-疲劳的修正系数模型，流程如图3所示。同样，对于磨损-疲劳问题，若磨损作用较小，但不可忽略，由于磨损导致结构强度降低，可以在疲劳模型的基础上，通过修正强度的方式引入修正系数，获得磨损-疲劳修正系数模型。

如对蠕变-疲劳故障，在热疲劳模型的基础上，考虑高温蠕变对寿命的影响，引入包含温度t、工作时间t影响的修正系数λ(t，t)进行修正，则蠕变-疲劳损伤等效物理模型为

式中，m、c为材料低周疲劳性能参数，m·为载荷级数，含下标i的项表示与第i级载荷条件下对应的量，如ni为第i级载荷水平的循环数，δεpi为该载荷水平的塑性应变幅值。模型的修正系数λ(t，t)，通过蠕变-热疲劳交互作用力学机理分析确定。α为损伤累积因子，当损伤累积达到该值时发生故障。

3参数化仿真

考虑到机械产品结构复杂，常用cae工具仿真分析应力、应变等响应。可靠性分析的求解是一个迭代的过程，需要利用cae工具计算不同参数输入对应的响应，因此应事先建立结构响应的参数化仿真模型。由结构主要影响因素，包括载荷、材料性能、结构尺寸等方面因素，确定主要参数，通过调整参数控制结构几何形状，自动实现损伤等效物理模型的重构，以便于多次仿真，进行随机性分析。

4故障物理模型随机性分析

在损伤等效物理模型的基础上，考虑影响因素分析所获得的材料参数、载荷、结构尺寸等参数随机性，利用抽样法、近似可靠度方法等，对物理模型进行随机性分析。根据结构因素的随机性和影响程度大小，因素可分两部分。一部分为随机参数，其随机性较大，或者对可靠性影响较大；另一类为常规参数，即不考虑其随机性。根据多故障机理损伤等效的物理模型，表示总损伤的通用式为

∑d＝f(x1，x2，…，xn)

式中，x1，x2，…，xn为物理模型的随机参数，分两类变量，一类变量，其变量值与随机性，可以直接通过因素分析获得，如材料参数、载荷、结构尺寸等；另一类，为结构响应变量，如结构温度、应力、应变(包括弹性应变、塑性应变、蠕变)，以因素变量作为输入，借助cae仿真或试验获得响应变量值及其随机性。函数f为利用损伤叠加或损伤修正的多故障物理模型。

由于x1，x2，…，xn中为随机变量，则总损伤∑d也为随机变量。对于简单的故障物理模型，通过概率运算方法，确定总损伤∑d的均值和标准差等分布参数。但多故障机理的物理模型一般较为复杂，需借助抽样法等确定总损伤∑d的分布参数，或者是使用代理模型获得显式函数。由此，多故障机理的结构可靠度为

r＝p{∑d≤α}＝p{α-f(x1，x2，…，xn)≥0}

式中，r为可靠度，p{·}表示概率。

结构寿命是随机变量x1，x2，…，xn的函数，因此寿命也是一个随机变量，结构寿命为

如由上述蠕变修正模型，得结构可靠度和寿命分别为

塑性应变幅值δεp为结构响应变量，其值和随机性往往无法直接获得，而且它与载荷、材料参数等有关，工程中一般需要借助cae工具获取。

5基于贝叶斯的模型随机性修正

寿命作为疲劳-蠕变、疲劳-磨损等耗损性故障的表征参数之一，根据工程经验，常将先验分布取为对数正态分布、威布尔分布、正态分布等。在研制过程中，结合单个试件试验，装备的初样试验、正样试验等的数据，利用贝叶斯更新理论，更新得到后验分布。在装备使用过程中，亦可依据现场维修、监测数据或实验数据再一次更新，得到模型或设计参数的最终后验分布，流程如图4所示。从而能够确定寿命分布，由此计算给定时间对应的可靠度以及可靠寿命。下面以蠕变修正模型为例，说明模型随机性修正过程。由等效物理模型

n＝c·(λ(t，t)·δεp)^-m

若塑性应变幅度δεp与载荷、材料参数、结构尺寸等的函数关系为

δεp＝h(e，f，α)

式中，h为拟合的响应面函数，e为弹性模量，f为载荷，α为材料热膨胀系数。若参数c、m、e、f、α均为随机量，为方便表示，统一为向量p表示(p1、p2、p3、p4、p5)。蠕变修正模型预测寿命表示为

n＝f(p1，p2，…，p5)

若通过试验获得寿命数据样本nt，s为寿命值的自然对数标准差，并将寿命的先验分布假定为对数正态分布，则可以给出对数正态似然函数

由各随机变量的分布及其参数，通过马尔科夫链蒙特卡洛仿真等可得到寿命的后验分布。