一种自适应RBF神经网络进行航空发动机推力估计算法的制作方法

本发明涉及航空发动机推力估计方法，属于数据回归分析、发动机控制、推力控制及估计等
技术领域：
。
背景技术：
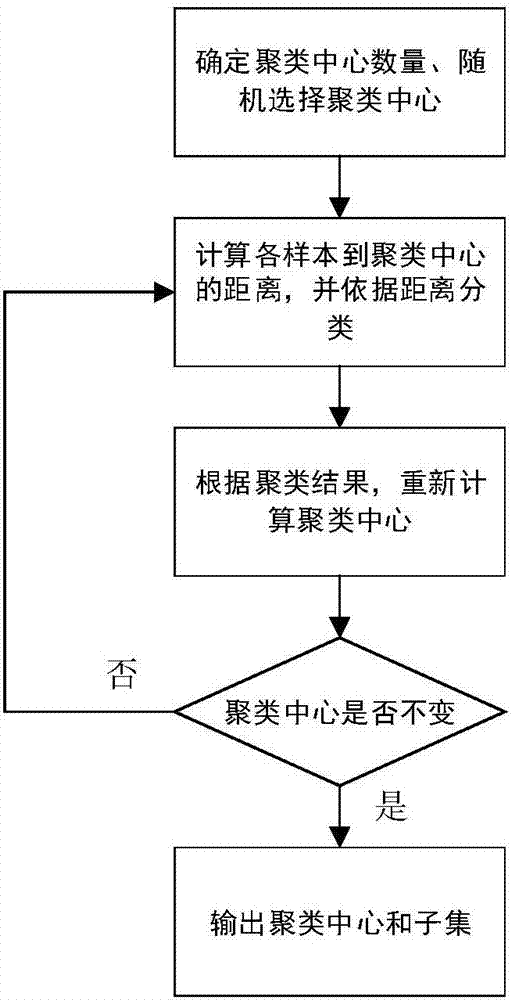
：在飞行器控制系统设计中，控制航空发动机的主要目的是控制其推力，但发动机推力在飞行中是不可测量的量。航空发动机不可测性能参数估计一直是航空领域备受关注的课题，航空发动机的推力作为航空发动机参数中非常重要的部分，也一直是发动机不可测性能参数估计中深受重视的问题。传统控制常用的推力估计方法有直接推力估计方法和间接推力估计方法。直接推力估计方法通过某种算法，直接从发动机的可测参数获得发动的推力估计值，比如利用神经网络实现推力的直接估计。间接推力估计方法多基于机载发动机实时模型，认为机载发动机实时模型能代表额定状态下发动机的工作情况，在非额定状态，通过跟踪滤波器对真实发动机在使用中的健康参数蜕化进行估计，修正机载实时模型的健康参数，以修正后的发动机模型的计算推力值为真实发动机的推力估计值。目前国内外都已开展了发动机推力估计的方法研究。在直接推力估计方法方面，2003年maggiorem,ordonezr,passionkm等在engineeringapplicationsofartificialintelligence上发表了“estimatordesigninjetengineapplication”，提出了一种基于神经网络的估计器，用于估计发动机推力、喘振边界和其他不可测性能参数，但该方法不涉及神经网络的参数和网络结构的优化过程，参数的确定和隐含层节点数的选择需要人为确定；2007年姚彦龙和孙健国在航空动力学报上发表了“自适应粒子遗传算法在推力估计器中的应用”，提出了一种自适应遗传神经网络算法，通过自适应概率遗传操作及局部寻优算子直接优化出神经网络拓扑结构及权值(包括阈值)，再应用神经网络对上述优化的权值(包括阈值)进行"精调"，最后设计出全包线推力估计器。虽然该方法设计网络参数和网络规模的优化过程，但遗传算法的搜索速度比较慢，要得到精确的解需要较多的训练时间，且算法的编程实现比较复杂。2009年赵永平和孙健国在航空动力学报上发表了“最小二乘向量回归机在发动机推力估计中的应用”，详细介绍了利用最小二乘向量回归机解决推力估计问题的方法，此后该作者2010年在航空动力学报上又发表了“基于k-均值聚类和约简最小二乘支持向量回归机的推力估计器设计”，进一步丰富和完整了基于支持向量回归机的推力估计器设计方法。基于支持向量机的推力估计方法主要问题是，在数据量较大时，支持向量机的训练时间将大幅度增大。2017年宋汉强、李本威在“推进技术”中发表了“基于聚类与粒子群极限学习机的航空发动机推力估计器设计”，提出了利用粒子群算法寻优极限学习机的拓扑结构的方式来确定隐含层神经元数目，并应用于发动机地面状态推力估计。该方法结合了极限学习机的优点，但只对于网络拓扑结构进行了优化，缺少对网络参数的优化过程，使得算法对于网络的初始化有一定的依赖性。在间接推力估计方面，santanuc,jnoathansl在cleveland,ohio:nationalaeronauticsandspaceadministration,johnh.glennresearchcenteratlewisfield上发表了“onlinemodelparameterestimationofjetenginedegradationforautonomouspopulationcontrol”，提出了基于kalman滤波器的间接推力估计的方法。2011年李秋红，孙健国和王前宇在控制理论与应用(controltheory&application)上发表了“航空发动机推力估计新方法”，论文针对采用卡尔曼滤波器方法进行航空发动机推力估计时，在非设计点存在稳态跟踪滤波器误差的问题，提出了基于控制器跟踪滤波器的推力估计方法。上述基于卡尔曼滤波器的航空发动机推力估计方法，都存在原理复杂、实现难度大、参数估计不够稳定的缺点。技术实现要素：本发明针对目前航空发动机推力估计方法单一且精度有限的问题，提出一种推力估计的新方法，为航空发动机推力估计提供一种新思路，同时，也提高推力估计的精度。为实现上述目的，本发明采用如下技术方案：一种自适应rbf神经网络进行航空发动机推力估计的算法，包括如下步骤：步骤1：获取发动机机载设备的各项影响发动机推力的参数，以周期δt采集全飞行包线内所述参数的值以及发动机实际推力，构成数据集；步骤2：对步骤1所得数据集进行归一化处理，得到归一化处理后的数据集；步骤3：对步骤2所得归一化处理后的数据集应用k-means聚类算法，将其分成若干个子集；步骤4：将步骤3所得子集分成训练数据集和测试数据集；以训练数据集中除发动机实际推力外的数据作为输入，发动机实际推力作为输出，利用改进的粒子群算法训练rbf神经网络参数和网络规模，得到子集的rbf神经网络回归机；所述rbf神经网络回归机用以估计发动机推力；所述改进的粒子群算法以rbf神经网络回归机估计的发动机推力与实际发动机推力的相对误差的绝对值最小化作为优化目标；步骤5：训练rbf神经网络回归机，即根据子集的测试数据集，测试在给定粒子群算法参数下与子集对应的rbf神经网络回归机估计的发动机推力是否满足预定精度；如果满足预定精度，则当前粒子群算法的参数设定为子集的优化参数；如果不满足预定精度，则修改粒子群算法的参数，重复步骤4直至rbf神经网络回归机估计的发动机推力能够满足预定精度；步骤6：如果多次调整粒子群算法参数依然不能得到满足预定精度的rbf神经网络参数和网络规模，则针对所有不满足预定精度的数据构成的数据集重复步骤3至步骤5。进一步的，步骤1中获取发动机机载设备的各项影响发动机推力的参数包括如下步骤：步骤1.1：以周期δt采集全飞行包线内发动机机载设备的各项参数的值；步骤1.2：对步骤1.1所得数据进行预处理，去除有缺失和明显不合理的数据；步骤1.3：利用特征选择算法从步骤1.2所得数据中提取出对发动机推力影响大的参数。进一步的，所述影响发动机推力的参数包括：发动机所处高度、发动机飞行马赫数、发动机外涵出口总压、发动机喷口截面参数、发动机主燃油量、发动机加力供油量、发动机的温比。进一步的，步骤4中所述rbf神经网络回归机的建设包括如下步骤：步骤4.1：设置改进的粒子群算法参数，所述参数包括：4.1.1：隐含层节点数的最大值u和最小值l；4.1.2：迭代次数iter，局部迭代次数t，粒子个数g；加速常数c1、c2；惯性权重最大值wmax和最小值wmin；4.1.3：搜索空间[xmin,xmax]；4.1.4：粒子飞行速度范围[vmin,vmax]；4.1.5：输入数据的维数d和输入数据的个数n；步骤4.2：数据初始化，包括：4.2.1：粒子位置初始化；粒子位置的初始化包括两个部分，一部分是粒子的节点数k的值，根据以下公式产生：k＝round((u-l)*rand(g,1)+l)此处，k为一个g维的列向量，存储g个粒子位置的节点数；rand(g,1)表示在(0,1)之间产生g行1列均匀分布的随机数向量，g为粒子的个数，round表示取整函数；粒子位置初始化的另外一部分为中心向量的初始化，根据以下公式生成：center＝(xmax-xmin)*rand(g,u*d)+xmin此处rand(g,u*d)表示在(0,1)之间产生g行u*d列均匀分布的随机数矩阵，u*d表示节点数最大值u与输入数据维数d的乘积；采用以下方式増广矩阵center，组成最终的初始粒子群位置矩阵swarm：swarm＝[k,center]初始粒子群位置矩阵swarm有g行，代表g个粒子的位置，每个粒子位置的第一维为该粒子的节点数；4.2.2：粒子速度velocity初始化；速度的初始化采用以下公式：velocity＝(vmax-vmin)*rand(g,u*d+1)+vmin4.2.3：rbf神经网络隐含层rbf宽度的初始化；生成公式为：s＝(smax-smin)*rand(1,u)+smin或s＝(smax-smin)*rand(g,u)+smin此处smax为宽度的最大值，smin为宽度的最小值，rand(1,u)表示在(0,1)之间产生1行u列均匀分布的随机数向量，rand(g,u)表示在(0,1)之间产生g行u列均匀分布的随机数矩阵；步骤4.3：求解粒子群初始当前最优解pbest、局部最优解tbest和全局最优解gbest，求解过程如下：4.3.1：以初始粒子群位置swarm为当前最优解pbest，计算pbest每个粒子的适应度的值，所得的所有粒子的适应度值构成的向量记为fitness；4.3.2：初始局部最优解tbest；根据粒子群的节点数k将所有粒子分类，分类数量为(u-l+1)，此处u为节点数的最大值，l为节点数的最小值；然后计算每一类中所有粒子的适应度的值，适应度值最小的粒子为该类的局部最优解；4.3.3：初始全局最优解gbest；当前最优解pbest中适应度值最小的粒子即为全局最优解；步骤4.4：以上步骤后，进行以下循环：4.4.1：迭代计数器t设置为t＝1；4.4.2：计算惯性权重w，计算公式如下：w＝(wmax-wmin)*(iter-t)/iter+wmin4.4.3：针对第i(i＝1,2…g)个粒子，进行以下子循环：1)判断是否t<t，若判断结果为真，则选择该粒子的有效节点数为该粒子的节点数，记为node；最优粒子best取节点数为node的类的局部最优解；若判断结果为假，则选择有效节点数为全局最优解gbest、该粒子的当前最优解pbest(i)和该粒子当前位置swarm(i)节点数的最大值作为第i个粒子的有效节点数node，而best＝gbest；2)计算有效维度，采用以下公式active_dimen＝node*d+1；此处active_dimen表示有效维度；3)根据以下公式更新粒子：volecity(i,j)new＝w*volecity(i,j)+c1*rand*(pbest(i,j)-swarm(i,j))+...c2*rand*(best(j)-swarm(i,j))swarm(i,j)new＝swarm(i,j)+volecity(i,j)new此处volecity(i,j)表示第i个粒子的速度的第j维分量，j＝1,2…active_dimen，volecity(i,j)new为更新后的速度分量；w为惯性权重，c1和c2为加速常数；rand表示产生一个(0,1)之间均匀分布的随机数，pbest(i,j)为第i个粒子当前最优解的第j维分量，swarm(i,j)为第i个粒子位置的第j维分量，swarm(i,j)new为更新后的粒子对应的位置分量；best(j)为步骤1)中的最优粒子best的第j维；4)限制粒子swarm(i,j)和volecity(i,j)new的范围，采取以下公式：当j不为1，即swarm(i,j)不为节点数时，swarm(i,j)new＝(xmax-xmin)*rand+xmin当swarm(i,j)<xmax或者swarm(i,j)>xmax当j为1，即swarm(i,j)为节点数时，调整节点数为整数，采用以下公式：swarm(i,1)new＝ceil(swarm(i,1))此处，ceil表示向上取整函数；5)根据适应度函数，计算更新后的粒子的适应度值fitnew；6)若第i个粒子的当前最优粒子的适应度值fitness(i)大于该粒子更新后的适应度值fitnew，则更新pbest(i)和适应度值fitness(i)，公式如下:pbest(i)＝swarmnew(i)fitness(i)＝fitnew此处swarmnew(i)为更新后的第i个粒子的位置；若fitness(i)<fitnew，不更新pbest(i)和fitness(i)；7)若t<t，则判断fitnew是否小于第i个粒子所在的类的局部最优解的适应度值，若判断为真，则该类的局部最优解更新为swarmnew(i)，该类局部最优解的适应度值更新为fienew；否则，不更新；8)根据第i个粒子的有效维度，重新初始化该粒子除有效维度部分外的位置分量；4.4.4：更新全局最优解gbest及其适应度值，更新的方法为：取fitness最小值为gbest的适应度的值，且与该最小值对应的当前最优粒子为gbest；4.4.5：更新迭代计数器t，t＝t+1；若t>iter，退出循环；否则返回步骤4.4.2。进一步的，所述rbf神经网络回归机估计发动机推力包括如下步骤：a)根据选定的粒子位置中的节点数k0和输入数据的维数d，从该粒子位置中提取出中心向量；首先从粒子的位置向量中截取第2维至第(k0*d+1)维的数据；然后按照顺序每d个数据取为一个中心，总共提取出k0个中心，即cj,j＝1,2,…,k0；b)根据步骤4.2中初始化的rbf神经网络隐含层rbf的宽度s，选取s的前k0个值，分别作为与k0个中心向量对应的宽度，即sj,j＝1,2,…,k0；c)根据训练数据的输入数据和提取出的k0个中心、宽度sj计算隐含层输出，即为h；此处，xi指第i个输入数据，cj指第j个中心，sj指第j个隐含层rbf的宽度，指第j个隐含层rbf在第i个输入数据下的输出值，n0为输入数据的个数；||·||指向量的2-范数；d)根据隐含层输出h和训练数据的输出，通过广义逆计算权重向量weight，记训练数据的输出，即归一化后的实际推力为y，则公式如下：weight＝h+y此处h+表示h的广义逆；e)根据以下公式计算rbf神经网络回归机估计的推力：netthrust＝h*weight进一步的，所述粒子的适应度值的计算包括如下步骤：步骤ⅰ：反归一化网络估计的推力netthrust和归一化后的实际推力y得到反归一化后的推力thrustnet和thrustreal；根据下述公式反归一化网络估计的推力netthrust和归一化后的实际推力y：thrustnet＝(fmax-fmin)*netthrust+fminthrustreal＝(fmax-fmin)*y+fmin此处，fmax、fmin分别为发动机实际推力的最大值和最小值；步骤ⅱ：计算每个输入的网络估计的推力与实际推力的相对误差的绝对值并取相对误差的最大值记为rd，公式如下：步骤ⅲ：粒子的适应度值依据以下公式计算：fitness＝α*k+rd此处，k为粒子的有效节点数，α为预先设定的参数，用于调整网络规模。进一步的，步骤5中所述发动机推力是否满足预定精度以rd的大小为判断依据，若rd小于预定精度，则训练过程结束；否则，调整粒子群算法的各项参数，重新训练。进一步的，步骤6的具体步骤如下：步骤6.1：将所有多次调整粒子群算法参数后仍不能获得满足精度的数据子集合并为一个数据集；步骤6.2：重新确定聚类中心数量；步骤6.3：根据聚类算法对新的数据集聚类。本发明的有益效果为：本发明提出的方法，利用改进后的粒子群算法同时优化神经网络的参数和网络规模，充分发挥粒子群算法快速逼近最优解的优点，实现利用更紧凑的神经网络更精确地估计航空发动机的推力。相对于现有的推力估计方法而言，本发明具有以下优点：1、提出了推力估计的一种新方法和新思路；2、方法易于理解，且算法的参数调整简单；3、方法易于实现，适用性强，可实现高精度推力估计。附图说明图1为本发明算法的整体流程图；图2为k-means聚类算法流程图；图3为改进的粒子群算法训练rbf神经网络回归机流程图；图4为rbf神经网络回归机参数调整过程；图5.1-图5.12为各子集的粒子群算法适应度；图6.1-图6.12为各子集隐含层节点图；图7.1-图7.12为各子集的相对误差。具体实施方式本发明公开了一种自适应rbf神经网络进行推力估计的算法。本算法主要特点是，利用改进的粒子群算法优化径向基函数神经网络的各节点的中心、宽度和连接权重等神经网络参数，同时优化网络规模，以实现在满足精度要求的情况使得神经网络更加紧凑。本算法可以用于中小规模的数据回归问题，在航空发动机方面，可以用于推力等参数的估计。本发明基于粒子群算法提出了自适应rbf神经网络。在改进的粒子群算法中，针对不同的网络隐含层节点数，设置与隐含层节点数种类个数相同的局部最优解。包括如下步骤：利用航空发动机机载设备的各项参数的输出数据，例如油门杆角度、高度、马赫数、风扇相对转速、压气机相对转速等，利用特征选择算法，选取影响发动机推力的主要参数；针对特征选择算法处理后的数据，进行数据归一化处理；针对归一化后的数据，进行k-均值聚类，确定每类数据的训练数据和测试数据，并存储聚类中心；针对分组后的数据，对每一组数据应用改进后的粒子群算法优化确定径向基函数神经网络的参数和网络的规模，训练得到每组数据对应的紧凑的子rbf神经网络回归机；对于一个新的输入数据，归一化处理后，根据该数据与已知聚类中心的距离确定对应的子rbf神经网络回归机，估计新输入发动机数据下的推力。具体包括以下步骤：1)以周期δt获取发动机机载设备的各项参数的输出数据，并整理存储。数据应尽可能覆盖发动机飞行的全包线等各种情况；2)数据预处理。分析并处理所获得的数据中有缺失和明显不合理的数据；3)根据特征选择算法分析数据，提取相对而言对推力影响大的重要特征，并整理特征选择后的数据；4)对特征选择后的数据集，进行归一化处理，归一化方法采取以下方法将所有特征归一化到区间[0,1]：此处，xmin是需要归一化的特征x的最小值，xmax是该特征x的最大值。x_new是归一化后的特征。5)对归一化后的特征数据，应用k-means聚类算法，将数据集分成一定个数的小数据集，使得具有相同特点的数据处于一个相同的子集。6)针对每一个子集，确定该数据集的训练数据集和测试数据集。训练数据集用于rbf神经网络回归机的训练，测试数据集用于测试训练得到的rbf神经网络回归机估计的精度。7)以训练数据中除推力外的特征作为输入，推力作为输出，利用改进的粒子群算法针对每个子集，训练rbf神经网络参数和网络规模，得到该子集的rbf神经网络回归机，以使得网络预测的推力与实际推力之间的相对误差尽可能小的同时，所需要的隐含层节点数尽也可能少。粒子群算法以径向基函数神经网络回归机估计的推力与实际推力的相对误差的绝对值最小化作为优化目标。8)根据各子集的测试数据集，测试在给定粒子群算法参数下的与该子集对应rbf神经网络回归机估计的推力是否满足预定精度。如果满足预定精度，则当前粒子群的参数设定为该子集的优化参数；如果不满足给定参数，则修改粒子群的参数，重新训练网络以使得新参数下的粒子群算法优化得到的rbf神经网络的推力估计能够满足预定精度。9)如果多次调整粒子群算法参数依然不能得到满足预定精度的rbf神经网络参数和规模，则需要针对那些不满足预定精度的数据重新进行聚类，以解决初始聚类不合理的问题。然后针对新聚类的子集，以同样的方式，通过粒子群算法优化得到rbf神经网络回归机，并适当调整粒子群算法参数，实现预定精度的推力估计。所述步骤3)中特征选择算法，可以选择主成分分析算法等现有算法，进行数据的特征选择。所述步骤4)中数据归一化处理的具体步骤是：a)针对数据的每个特征，找到该特征的最大值xmax和特征的最小值xmin；b)根据步骤a)中获得最大值和最小值，对于该特征的每个值x，应用下面的式子，归一化该特征得到x_new：所述步骤5)中k-means聚类算法的具体步骤如下：a)从数据集中随机选取k个样本，作为所需分成的k个子集的初始中心；b)分别计算所有样本到k个子集各自的中心的距离，将这些样本分别划归到距离最近的子集中。这里所说的某个样本x与某个中心ui距离计算公式如下：这里n为x的维度，xj为样本x的第j维，uij为第i个子集中心的第j维。c)根据聚类得到的子集，重新计算k个子集各自的中心，计算方法是取子集中所有样本各自维度的算术平均值；d)将数据集中的全部样本按照新的k个中心重新聚类；e)重复步骤d)直到聚类结果不再变化；f)输出聚类结果；所述步骤6)中选取训练数据集和测试数据集的具体步骤如下：a)确定训练数据集和测试数据集各自所占总数据集的比例，比如数据集中每四个数据选择三个数据作为训练数据，余下的一个为测试数据；b)针对数据集以归一化后的推力从小到大排序；c)依据步骤a)中确定的比例，从排序后的数据集中均匀选取训练数据集和测试数据集。比如当训练数据集规模和测试数据集规模为3:1时，以四个数据为一组，将数据集分组；选择每组的前三个数据为训练数据，每组的最后一个数据为测试数据。如果数据的选择方式不能取得好的训练结果，则需修改数据选取方式，比如每组的后三个数据作为训练数据集，而每组的第一个数据作为测试数据。d)如果以上用排序的方式选取数据的方法不能取得好的训练结果，则可以先确定训练数据的个数，直接从数据集中随机选取。所述步骤7)中的利用改进后的粒子群算法优化径向基函数神经网络回归机是该发明的核心部分，其原理和步骤如下：原理：对于一个rbf神经网络回归机而言，其建立需要的参数为：隐含层节点数node，节点的中心center、宽度spread，以及隐含层输出与目标输出的连接权重weight。针对上述参数，在改进的粒子群算法中，每个粒子的初始化包括两个部分，一部分是一个在设定的范围[l,u]内随机产生的整数，此处记为节点数k，k标志了该粒子代表的神经网络回归机的隐含层节点数；另一部分是在[0,1]随机产生的向量，其维数为k*d，此处d为输入数据的维度。为了统一粒子的初始化，一般统一初始化粒子为(u*d+1)维，此处u为隐含层节点范围的最大值。一般把节点数k置于粒子的第一维上，定义(k*d+1)为有效维度，可知每个粒子的有效维度由粒子中的节点数k决定。由上述过程，可以确定每个粒子所代表的网络的隐含层节点数node和节点中心center。网络的宽度spread是预先随机生成的，且生成后不再改变。而网络的权重weight是根据已知的center、node和spread计算出隐含层输出与已知的训练数据的输出，通过广义逆求解的。在粒子群优化过程中，算法不断迭代，节点的中心向量和网络的节点数不断改变，相应的网络的宽度的维度和权重的数值以及规模不断改变，最终得到在所设定的参数下最优解。因此，粒子群算法不直接优化网络的权重向量，而是通过优化网络的中心，间接地优化权重向量，通过粒子群优化和理论计算结合的式以求得最优解。由以上过程可知，不同的粒子，可能具有不同的节点数k，这使得每个粒子的有效维度可能不同。在粒子群算法的优化过程中，全局最优解的节点数与单个粒子的节点数可能不同，针对此问题，对粒子群算法作以下两点改进。其一，对粒子中所有的节点数分类，针对每一个节点数，求取有与该节点数相同节点数的粒子局部最优解；设置局部迭代次数t，使得算法在t次迭代之前，针对每一类节点数的粒子，以局部最优解和粒子的当前最优解更新速度。而在t次迭代之后，以全局最优解和粒子的当前最优解更新速度；其二，t次迭代之后，全局最优解的有效维度与单个粒子的有效维度可能不同。因此，选择全局最优解、单个粒子和粒子当前最优解的有效维度的最大值作为需要更新的部分。在优化过程中算法每次迭代完成后，重新初始化每个粒子有效维度之外的部分，以尽量避免粒子更新带来的干扰。具体步骤如下：由步骤6)得到的归一化后的训练数据集，选择归一化后的推力作为网络输出，其余特征作为网络的输入；参数设置，包括以下部分：a)设置隐含层节点数的最大值u和最小值l，粒子群算法通过在此范围内优化得到满足预定精度下的隐含层节点数，构建紧凑的rbf神经网络回归机；b)迭代次数iter，局部迭代次数t，粒子个数g。加速常数c1、c2，一般都设置为1.49。惯性权重最大值wmax和最小值wmin，一般设置为wmax＝0.9，wmin＝0.4；c)搜索空间[xmin,xmax]，在推力估计中，数据归一化在[0,1],因此设置xmin＝0，xmax＝1；d)粒子飞行速度范围[vmin,vmax]，速度范围的设置与搜索空间有一定联系。一般来说vmin＝-vmax，在推力估计中，设置vmax＝k*xmax，k的值在0到1之间，且不应太大；e)由训练数据集的输入数据得到输入数据的维数d和输入数据的个数n；数据初始化，包括以下部分：a)粒子初始化。粒子的初始化包括两个部分，一部分是该粒子的节点数k的值，根据以下公式产生：k＝round((u-l)*rand(g,1)+l)此处rand(g,1)表示在(0,1)之间产生g行1列均匀分布的随机数向量，g为粒子的个数，round是取整函数，用于得到整数的节点数。粒子初始化的另外一部分为中心向量的初始化，统一采用以下公式生成：center＝(xmax-xmin)*rand(g,u*d)+xmin此处rand(g,u*d)表示在(0,1)之间产生g行u*d列的随机数矩阵，u*d表示节点数最大值u与输入数据维数d的乘积；将k向量置于矩阵center第一列内，组成最终的初始粒子群swarm；b)粒子速度velocity初始化。速度的初始化采用以下公式：velocity＝(vmax-vmin)*rand(g,u*d+1)+vminc)rbf神经网络隐含层节点宽度的初始化。网络节点宽度随机产生，有两种形式。一种形式的公式如下：s＝(smax-smin)*rand(1,u)+smin此处smax为宽度的最大值，smin为宽度的最小值，rand表示产生(0,1)之间的随机数。这种形式针对所有粒子使用随机产生的相同的宽度；另一种形式是：s＝(smax-smin)*rand(g,u)+smin这种情况针对不同的粒子使用随机产生的不同宽度。粒子初始当前最优解pbest、局部最优解tbest和全局最优解gbest，求解过程如下：a)以初始粒子群位置swarm为当前最优解pbest，计算pbest每个粒子的适应度的值，所得的所有粒子的适应度值构成的向量记为fitness；b)初始局部最优解tbest。根据粒子的节点数k将所有粒子分类，一般类的数量为(u-l+1)，此处u为节点数的最大值，l为节点数的最小值。然后计算每一类中所有粒子的适应度的值，适应度值最小的粒子为该类的局部最优解；c)初始全局最优解gbest。当前最优解pbest中适应度值最小的粒子即为全局最优解。以上步骤后，进行以下循环a)迭代计数器t设置为t＝1；b)计算惯性权重w，计算公式如下：w＝(wmax-wmin)*(iter-t)/iter+wminc)针对第i(i＝1,2…g)个粒子，进行以下子循环：1)判断是否t<t，若判断结果为真，则选择该粒子的有效节点数为该粒子的节点数，记为node。最优粒子best取节点数为节点数为node的类的局部最优解；若判断结果为假，则选择有效节点数为全局最优解gbest、该粒子的当前最优解pbest(i)和该粒子swarm(i)有效节点的最大值作为第i个粒子的有效节点数node，而best＝gbest；2)计算有效维度，采用以下公式active_dimen＝node*d+1；此处active_dimen表示有效维度；3)针对该粒子的有效维度active_dimen，根据以下公式更新粒子：volecity(i,j)new＝w*volecity(i,j)+c1*rand*(pbest(i,j)-swarm(i,j))+...c2*rand*(best(j)-swarm(i,j))swarm(i,j)new＝swarm(i,j)+volecity(i,j)new此处volecity(i,j)表示第i个粒子的速度的第j维分量，j＝1,2…active_dimen，volecity(i,j)new为对应的更新后的速度分量。w为惯性权重，c1和c2为加速常数。rand表示均匀产生(0,1)之间的随机数，pbest(i,j)为第i个粒子当前最优解的第j维分量，swarm(i,j)为第i个粒子的第j维分量，swarm(i,j)new为更新后的粒子。best(j)为步骤(1)中的最优粒子best的第j维；4)限制粒子swarm(i,j)和volecity(i,j)new的范围，采取以下公式：当j不为1，即swarm(i,j)不为节点数时，swarm(i,j)new＝(xmax-xmin)*rand+xmin当swarm(i,j)<xmax或者swarm(i,j)>xmax当j为1，即swarm(i,j)为节点数时，须调整节点数为整数，采用以下公式：swarm(i,1)new＝ceil(swarm(i,j))此处，ceil表示对swarm(i,j)向上取整。此外，为限制swarm(i,1)new属于[l,u]之间，采用以下公式：5)根据适应度函数，计算更新后的粒子的适应度值fitnew；6)若第i个粒子的适应度fitness(i)大于该粒子更新后的适应度fitnew，则更新pbest(i)和适应度fitness(i),公式如下:pbest(i)＝swarmnew(i)fitness(i)＝fitnew此处swarmnew(i)为更新后的第i个粒子；若fitness(i)<fitnew，不更新pbest(i)和fitness(i)；7)若t<t,则判断fitnew是否小于第i个粒子有效节点所在的类的局部最优解的适应度值，若判断为真，则该类的局部最优解更新为swarmnew(i)，该类局部最优解的适应度值更新为fienew；否则，不更新；8)根据第i个粒子的有效维数，重新初始化该粒子除有效维数部分外的部分；d)更新全局最优解gbest及其适应度值，更新的方法为：取fitness最小值为gbest的适应度，且与该最小值对应的pbest为gbest；e)更新迭代计数器t，t＝t+1；若t>iter，退出循环；否则返回步骤(b)。上述步骤所述适应度函数介绍如下：适应度函数的输入为单个粒子，训练数据集的输入数据和输出数据，随机产生的宽度向量s(若每个粒子的宽度向量不同，则第i个粒子的宽度向量为s(i))。适应度函数的输出为网络估计的推力与实际推力的相对误差的绝对值的最大值。粒子群算法的优化目标是使得相对误差的绝对值尽可能小。适应度函数的计算步骤如下：a)根据选定的粒子位置中的节点数k0和输入数据的维数d，从该粒子位置中提取出中心向量；首先从粒子的位置向量中截取第2维至第(k0*d+1)维的数据；然后按照顺序每d个数据取为一个中心，总共提取出k0个中心，即cj,j＝1,2,…,k0；b)根据初始化的rbf神经网络隐含层rbf的宽度s，选取s的前k0个值，分别作为与k0个中心向量对应的宽度，即sj,j＝1,2,…,k0；c)根据训练数据的输入数据和提取出的k个中心、宽度计算隐含层输出，即为h；此处，xi指第i个输入数据，cj指第j个中心，sj指第j个隐含层rbf的宽度，指第j个隐含层rbf在第i个输入数据下的输出值，n0为输入数据的个数；||·||指向量的2-范数；d)根据隐含层输出h和训练数据的输出，通过广义逆计算权重向量weight,若记训练数据的输出为t(即归一化后的推力)，则公式如下：weight＝h+t此处h+表示h的广义逆。e)根据以下公式计算网络估计的推力：netthrust＝weight*hf)反归一化网络估计的推力和实际推力t得到反归一化后的推力thrustreal和thrustnet。反归一化的公式如下：x＝(xmax-xmin)*x+xmin此处，xmax和xmin为归一化过程中的特征x的最大值和最小值，而x为需要反归一化的数据。反归一化网络估计的推力netthrust和归一化后的实际推力y：thrustnet＝(fmax-fmin)*netthrust+fminthrustreal＝(fmax-fmin)*y+fmin此处，fmax、fmin分别为发动机实际推力的最大值和最小值。g)计算每个输入的估计的推力与实际推力的相对误差的绝对值，公式如下：h)该粒子的适应度fitness则依据以下公式计算：fitness＝α*k+rd此处，k为该粒子的有效节点数，α为预先设定的参数，其作用是控制rbf神经网络的规模，通过调整α的大小，可以调节网络的节点数，使得网络更加紧凑。所述步骤(8)的具体过程如下：a)将测试数据集中除推力外的特征作为输入量，注意输入量的特征需要与训练数据的输入量的特征对应。将数据输入到粒子群算法优化得到的径向基函数神经网络回归机，得到估计的推力；b)计算估计的推力与实际推力反归一化的相对误差的绝对值；c)判断误差的绝对值是否小于给定的精度；若小于给定的精度，则训练过程结束；否则，调整粒子群算法的各项参数，重新训练。d)粒子群算法参数的调整顺序一般为：径向基函数节点的宽度w、迭代次数iter和粒子数量n，除此之外的其他参数，在针对一个子集调整后，再处理其他子集时，一般不需要修改。一般情况下，网络节点的宽度w过小，会导致隐含层输出过小，在计算网络的权重矩阵时会产生较大误差。在发动机推力估计问题里，一般设置w在0.7-1.2之间随机产生。所述步骤(9)中针对初次聚类不合理的子集重新聚类的具体步骤如下：a)将所有多次调整粒子群算法参数后仍不能获得满足精度的数据子集合并为一个数据集；b)重新确定聚类中心数量，一般需要选取比合并的子集数量大一些的中心个数；c)根据聚类算法对新的数据集聚类。实施例：发动机数据基本信息：实施例所采用的发动机数据采集自一种混合排气加力式双轴涡轮风扇发动机，其主要部件有：进气道、风扇、压气机、高压涡轮、低压涡轮、外涵、加力燃烧室和尾喷管等。数据集的采集涵盖发动机的全飞行包线，数据集包含27395个样本数据，每个采样时刻采集49个参数的数值，包括油门杆角度、高度、马赫数、风扇相对转速、压气机相对转速等，但大多数参数存在冗余。本发明不涉及特征选择的具体过程，因此特征选择过程在此不作叙述。经过特征选择后，选取以下七个特征作为推力估计的主要特征：高度、马赫数、外涵出口总压、喷口界面参数、主燃油量、加力供油量、发动机的温比。发动机的推力作为待估计的量。根据k-means聚类方法可以得到以下12个子集，其具体过程如下：首先设置聚类中心数量为10，得到10类；通过粒子群算法训练网络，发现有4个子集多次调整参数仍难以得到满意的结果；针对这4个子集的并集，设定聚类中心数量为6，重新聚类，两次聚类一共12类。得到的结果如下：表格1：实例的子集信息设置网络的参数，表格2的参数在针对第一个子集调整后，训练其他字集时，不需要再作调整。表格2：算法的固定参数(指这些参数在所有子集中都一样)参数c1c2wmaxwminxmaxxmintitergsmaxsmindα数值1.491.490.90.410301002501.20.571e-4表格3是针对不同子集，训练数据和测试数据的不同选择方式、以及u和l的设置方式表格3：算法的不同参数(指这些参数针对不同子集略有不同)子集数据选取方式节点数最小值l节点数最大值u#1[1,0,1,1]90100#2[1,1,1,0]6070#3[1,1,1,0]6070#4[1,1,1,0]6070#5[1,0,1,1]6070#6[1,1,1,0]6070#7[1,0,1,1]100110#8[1,1,1,0]5060#9[1,0,1,1]200210#10[1,0,1,1]200210#11[1,1,0,1]200210#12[1,0,1,1]200210注：[1,0,1,1]表达的意思是：针对训练数据，根据推力大小排序，然后依据顺序没四个为一组，选择每组的第1,3,4个数据作为训练数据，第2个数据作为测试数据，其余表达的意思类似；表格4：估计推力与实际推力的相对误差子集最小值/min最大值/max均值/mean方差/std测试时间/ms#13.12e-072.5e-033.17e-043.40e-040.0169#27.06e-071.8e-033.37e-042.75e-040.0149#32.04e-061.7e-035.10e-043.68e-040.0135#46.25e-072.3e-034.13e-043.54e-040.0136#52.13e-062.4e-034.31e-043.40e-040.0183#63.26e-061.7e-033.79e-043.20e-040.0345#71.30e-083.0e-032.57e-043.41e-040.0177#88.87e-072.2e-034.37e-043.56e-040.0178#94.79e-082.8e-032.41e-043.47e-040.0528#103.95e-042.0e-031.04e-041.67e-040.0336#111.17e-072.9e-032.17e-043.96e-040.0358#121.46e-081.7e-031.61e-042.63e-040.0411表格五：训练结果的各子集rbf神经网络隐层节点数子集#1#2#3#4#5#6#7#8#9#10#11#12节点数90626166606310159202200202204各子集的粒子群算法适应度如图5.1-5.12所示，各子集隐含层节点图如图6.1-6.12所示，各子集的相对误如图7.1-7.12所示。从以上结果可知：a)当子集的推力波动较大，即子集推力的方差较大时，rbf神经网络回归机需要更多的隐含层节点数，才能产生较好的估计结果；这也表明，可以参考聚类的数据特征，指导算法的参数调整，这使得算法的参数调整更加容易。b)若需要提高推力估计的精度，可以简单地通过增加节点数产生。c)从以上算法参数的调整方式来看，针对不同的数据集所需要调整的参数只有u和l以及数据的选取方式，不需要大量调整参数。当前第1页12