一种空间影像的高精度几何校正方法与流程

本发明涉及一种空间影像的高精度几何校正方法，属于机器人视觉、测绘与遥感以及工业测量等技术领域。

背景技术：

针对在立体空间多角度多采集的图像进行几何校正，目前主要有基于地面控制点的近似方法和基于位置姿态数据的校正方法，两种方法根据具体实施的不同需求和实际情况有所不同。

针对不同情况的几何校正，目前国内外有一定程度的研究。采用不同次数的多项式模型，不同数目的控制点对像片进行几何纠正，并对纠正精度进行比较，认为在观测基准面或平面、地面等较平坦的地区，多项式模型具有较好的拟合精度；有人利用gps数据对点摆式传感器图像进行了几何校正，只能达到粗校正的效果；对无人机平台下线阵最优的高光谱影像的变形研究的比较少；imu/dgps(惯性测量单元/差分gps)组合系统直接定位(directgeoreferencing,dg)外方位元素参数的方法虽然优于传统的空中三角测量，但其精度还是受到dgps、imu等仪器定标误差的限制。

本发明利用imu/dgps数据对空间影像进行几何校正，对于地面移动测量平台或者空中平台，可以达到高精度影像几何校正。

技术实现要素：

本发明公布了一种基于imu/dgps系统的、建立在共线方程的原理基础上的空间影像几何校正方法和步骤。为了达到上述目的，本发明的技术方案是这样实现的：

一种空间影像的高精度几何校正方法，包括以下步骤：

1)imu/dgps系统采集的数据与原始空间影像数据时间匹配处理；

2)通过坐标系转换求相机外方位元素；

3)原始空间影像数据与地面对应物方坐标的转化及最优扫描行列号匹配。

4)校正空间影像数据重采样，得到校正后空间影像。

所述步骤1)imu/dgps系统采集的数据与原始空间影像数据时间匹配处理，即按照时间转换关系，对imu/dgps系统采集数据或空间影像数据进行重采样，使imu/dgps系统采集数据的采样时间与空间影像数据的采样时间匹配；具体包括以下步骤：①将北京时间和格林尼治时间进行转换，实现时间基准统一；②在步骤①的两者时间基准统一的基础上，进行时间匹配。

所述步骤2)通过坐标系转换求相机外方位元素，包括以下步骤：①寻找像空间坐标系和地面成图坐标系转换的过渡坐标系；②基于步骤①中的一系列坐标系，求解相机外方位元素中的角元素，即旋转矩阵；③在步骤②的基础上，借助旋转矩阵，确定相机外方位元素中线元素。相机外方位元素包含角元素和线元素。

所述步骤3)原始空间影像数据与地面对应物方坐标的转化及最优扫描行列号匹配，包括以下步骤：利用摄影测量中的共线方程得到空间影像数据与对应地面实际坐标的对应关系，利用二分法寻找与地面实际坐标最为匹配的原始空间影像数据上的最优像元行列号(即最优扫描行列号)。

所述步骤4)按照步骤3)中获得的最优扫描行列号对原始像元重采样校正，得到校正后的空间影像数据。包括以下步骤：①预先创建被校正后的空白影像，对空白影像的每一个影像点进行灰度值赋值。赋值使用双线性内插方法，对空白影像逐个像点从原始影像数据上重采样从而得到新的灰度值。②重采样结束后保存为与原始影像大小相近的无几何变形影像。

与现有技术相比，本发明的优点在于：

1、利用imu/dgps给相机传感器提供位姿参数，可以进行实时连续作业，同时imu/dgps的差分精度比较高，在内插得到相机扫描行的几何参数数据时，精度更可靠。

2、在从地面反寻对应的扫描行的行列号时，使用二分法，极大的提高了寻找最优扫描行列号的效率。

3、可以适用于线阵扫描的任何传感器，包括可见、红外、单波段和多波段传感器。

4、应用领域广泛，不仅可以适用于机载，像无人机、气艇等平台，还可以应用于地面，像车载等平台。

附图说明

图1为本发明方法流程图；

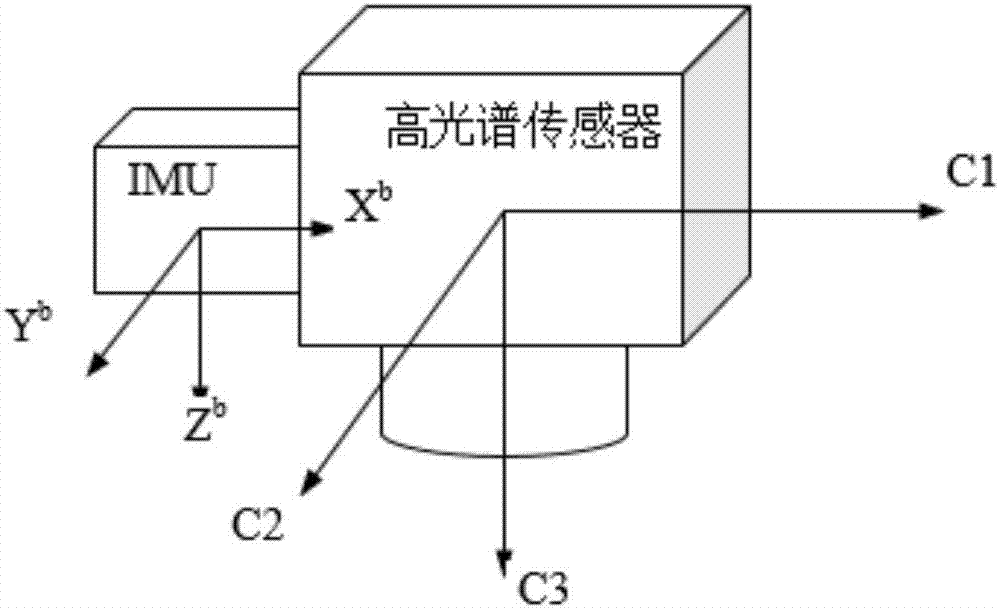
图2为imu及成像载荷传感器坐标系；

图3为像空间坐标系示意图；

图4为线中心投影；

图5为二分法确定最优扫描行方法流程图；

图6为本发明具体实施步骤流程图。

具体实施方式

下边结合图表/公式等，对本发明的具体实施步骤做详细说明。本发明方法步骤如图1所示。本发明的一种空间影像的高精度几何校正方法，包括以下步骤：

1.imu/dgps系统采集数据与空间影像数据时间匹配处理，包括以下步骤：

1)将北京时间和格林尼治时间进行转换，实现时间基准统一

成像载荷读取的时间是以北京时间为准，而imu/dgps输出的是格林尼治时间，所以在进行几何处理之前必须精确确定二者的转换关系，其换算公式为

imu/dgps_time＝(hour+16)×3600+minute×60+second(1)

式中，hour是原始影像数据的采样时间中的小时；同理，minute是分钟；second是秒。

2)在步骤1)的两者时间基准统一的基础上，进行时间匹配

imu/dgps的采样频率为每秒100次，而成像载荷数据的采样频率为每秒25条扫描行imu/dgps。所以需要根据imu/dgps系统采集数据与成像载荷的时间对应关系，对imu/dgps系统采集数据按成像光谱仪的空间影像数据记录频率进行最邻近重采样。

2.通过坐标系转换求相机外方位元素，包括以下步骤：

1)寻找像空间坐标系和地面成图坐标系转换的过渡坐标系

本发明所需的相机外方位元素(属于摄影测量坐标系统)与现有的imu/dgps导航解(属于惯性导航坐标系统)属于两个完全不同的系统，因此需要通过坐标转换在这两个系统间建立关系从而得到成像光谱相机的外方位元素。以下是对惯性导航坐标系统和摄影测量坐标系统的定义以及在求解外方位元素时所涉及的坐标系转换。

各坐标系定义如下：

成图坐标系(m)：用户根据飞行区域特点自定义的局部右手坐标系。

地心坐标系(e)：原点固定于地球中心，z^e轴指向北极，x^e轴指向赤道面与本初子午面的交点，y^e轴垂直于x^eoz^e平面。常用的地心坐标系为wgs-84大地坐标系。

导航坐标系(g)：原点位于飞行器质心，x^g为北方向(大地北)，y^g为东方向，z^g指向地心。坐标系统随飞行方向不断发生变化。

传感器坐标系(c)：原点位于透视中心，c2轴指向传感器右侧为正，c3轴指向地面方向为正，c1轴沿飞行方向前向为正。

imu坐标系(b)：以3轴加速度计的交点为原点，x^b轴指向飞行方向，y^b轴指向飞机右侧，z^b轴竖直向下形成右手坐标系。理想情况下，imu与高光谱传感器应紧密固联，imu坐标系与传感器坐标系只存在航向上的平移，但在实际中，imu坐标系与传感器坐标系间存在一定的交角，称为偏心角，这个偏心角需通过设立检校场来确定，见图2。

像空间坐标系(i)：以摄影中心s为坐标原点，x轴指向飞行方向，y轴指向影像左侧，z轴与主光轴重合，形成像空间右手直角坐标系s-xyz，见图3。

2)基于步骤1)中的一系列坐标系，求解相机外方位元素中的角元素，即旋转矩阵。

根据前述外方位元素的定义，像空间坐标系(i)可以看成是成图坐标系(m)依次经过绕y、x、z轴旋转角度ω、κ得到，这一过程可以分多步坐标系统变换完成，因此，成图坐标系(m)到像空间坐标系(i)的旋转矩阵可表示为：

其中(φ,θ,ψ)分别为侧滚角、俯仰角和偏航角。一旦确定了旋转矩阵和即可由上式解出外方位角元素ω和κ。

a)确定旋转矩阵成图坐标系(m)变换到地心坐标系(e)(wgs-84)

定义成图坐标系的原点位于飞行区域的中心，原点设为(b0,l0,0)，则由(m)到(e)的旋转矩阵可表示为：

b)确定旋转矩阵地心坐标系(e)变换到导航坐标系(g)

将地心坐标系变换到导航坐标系所形成的(e)到(g)的旋转矩阵可表示为：

其中，l和b分别为成像瞬间imu单元中心相位的经纬度。

c)确定旋转矩阵导航坐标系(g)变换到imu坐标系(b)

将导航坐标系变换到imu坐标系所形成的(g)到(b)的旋转矩阵可表示为：

d)确定旋转矩阵imu坐标系(b)变换到传感器坐标系(c)

将imu坐标系变换到传感器坐标系即纠正两个坐标系间存在的偏心角。假设偏心角在3轴方向上的分量分别θx，θy，θz，则旋转矩阵可表示为：

e)确定旋转矩阵传感器坐标系(c)变换到像空间坐标系(i)

传感器坐标系(c)到像空间坐标系(i)只是y、z坐标轴方向的不同，因此可表示为：

3)在步骤2)的基础上，借助旋转矩阵，确定线元素(xs,ys,zs)

在成像瞬间，传感器镜头透视中心在成图坐标系中的坐标可通过下式得到：

其中，(ximu,yimu,zimu)为imu坐标系(b)在wgs-84直角坐标系中的坐标；(x1,y1,z1)为传感器透视中心在imu坐标系中的偏心矢量；(x0,y0,z0)为成图坐标系原点(l0,b0)对应的地心直角坐标。

3.空间影像数据与地面对应物方坐标的转化及最优扫描行列号匹配，包括以下步骤：

1)空间影像数据与地面对应物方坐标的转化

由于空间影像中每一行上所有像元都是在同一时刻成像，因此在旁向(y方向)上可认为是中心投影关系。在垂直成像条件下，空间影像可简化为线中心投影处理，即同一扫描行上的像点具有相同的外方位元素，影像扫描行上像点与其对应地面真实点之间应满足以下共线方程：

其中，(x,y)为像点的像平面坐标，(x,y,z)为其对应地面点的大地坐标，f为相机主距，表示传感器外方位元素，满足线中心投影，如图4所示。

由式(9)和(10)所解得的(x,y)一般是浮点形式，对于重采样方法中涉及到的行列号(x',y')，则需做以下变换

上式中，psize为单个像元的大小。

2)基于步骤1)得到的原始空间影像数据与对应地面实际坐标的对应关系，利用二分法对最优扫描行列号匹配。

a)获取地面点成像的imu/dgps解。利用像点坐标的外方位元素及地面点坐标，结合共线方程(9)，通过求解无限收敛逼近x＝0，将此时所对应影像上的行作为最优扫描行，该行所对应的外方位元素作为地面点的外方位元素。

b)将地面点的外方位元素，地面点坐标代入公式(9)，计算得到地面点对应原始影像数据中的像点的列号，这样，就得到纠正后影像点(地面点)对应的原始影像数据的像点的位置信息，将其写入并保存到投影文件.prj中，将纠正后每行影像对应原始空间影像数据的行列范围写入并保存到索引文件.idx中。

重采样纠正的关键在于确定地面点的最优扫面行列号，进而得到该扫描行对应的外方位元素。地面点最优扫描行的判断依据是找到一组导航解带入公式(9)，使得所求x等于或者接近于0。最优扫面行列号的确定采用二分法实现。具体操作如图5所示。

二分法通过一步步缩小搜索范围来确定最优扫描行列号，包括如下步骤：

a)设定最优扫描行的初始值及搜索步长的初始变量。将最优扫描行l的初始变化参量l⁽⁰⁾设为n/2，由以上定义可知，搜索步长初始值可表示为n为原始空间影像数据的列数。

b)计算x值。分别将l⁽⁰⁾，所对应的外方位数据代入公式(9)，计算它们x值，记为x⁽⁰⁾，

c)确定l位置。判断的符号，若则l位于l⁽⁰⁾和之间，此时令若则l位于l⁽⁰⁾和之间，此时令

d)判断是否继续。若搜索步长(δ为给定阈值)，则继续下一步，否则返回第b)步。

e)确定最优扫描行列号。将搜索步长[ls,le]中每个扫描行的外方位元素代入公式(9)，计算x，xmin对应的扫描行即为最优扫描行。

4.校正像元重采样，得到校正后影像

1)使用双线性内插方法，对逐个影像点从原始空间影像数据上重采样从而得到新的灰度值；

双线性内插法是利用采样点q(u,v)周围邻近的4个像元值，按照其距内插点的距离赋予不同的权重进行线性内插，即

q(u,v)＝(1-s)(1-t)pi,j-(1-s)tpi,j+1+s(1-t)pi+1,j+stpi+1,j+1(12)

其中，

2)重采样结束后保存为与原始影像大小相近的无几何变形影像。

本发明的整个具体实施步骤，可以通过图6表示。

以上所述仅为本发明的较佳实施例，并不用以限制本发明，本领域的技术人员应可理解，凡在本发明的精神和原则之内所作的任何修改、等同替换或改进等，均应包含在本发明的保护范围之内，保护范围以权利要求书所界定者为准。