一种基于曲率单调变化的任意次Bezier曲线设计方法与流程

本发明涉及计算机辅助设计和计算机图形学技术领域，具体来说，涉及一种基于曲率单调变化的任意次bezier曲线设计方法。

背景技术：

曲率分布直接影响着曲线和曲面的形状，从艺术的角度来分析，曲率在曲线曲面光顺性方面扮演着重要角色。一般情况下，一条曲线如果具有相对较少的曲率单调变化的曲线段则被认为是光顺的。在工业设计中，这种概念也广泛被设计者所采纳。同时，曲率单调变化的曲线在道路设计、机器人轨道设计等领域被广泛应用。因此工业界的应用需求加速了关于曲率单调变化的曲线方面的研究。

bezier曲线在计算机辅助设计与计算机图形学中被广泛使用。目前，基于曲率单调变化的二次bezier曲线的研究比较充分，曲率单调的二次bezier曲线的设计方法也被提出。然而，对于曲率单调变化的高次bezier曲线的设计还存在困难，难以保证所生成曲线是曲率单调变化的。至今，现有技术没有给出如何构造曲率单调变化的高次bezier曲线。

技术实现要素：

针对相关技术中的上述技术问题，本发明提出一种基于曲率单调变化的任意次bezier曲线设计方法，改善现有技术的上述缺陷，可以用来进行艺术曲线的绘制设计，用于计算机辅助设计、交通线路设计、数字绘画等领域的技术实现。

为实现上述技术目的，本发明的技术方案包括以下步骤：

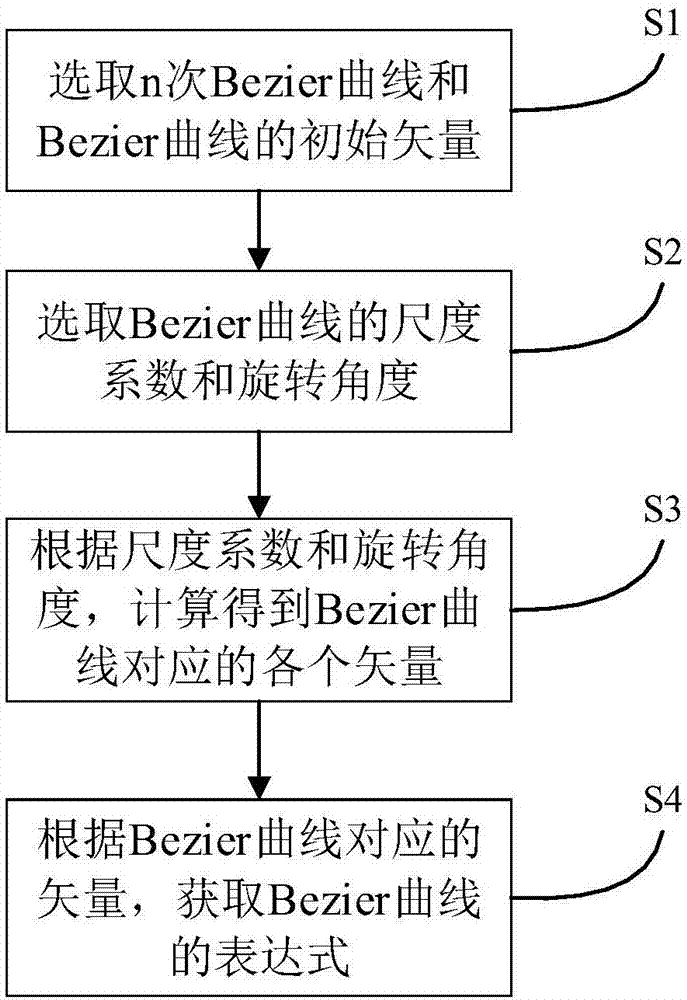
步骤s1：选取n次bezier曲线和所述bezier曲线的初始矢量v0；

步骤s2：选取所述bezier曲线的尺度系数s和旋转角度θ；

步骤s3：根据所述bezier曲线的尺度系数s和旋转角度θ，依次计算得到所述bezier曲线对应的矢量v1,v2,…,vn-1；

步骤s4：根据所述bezier曲线对应的矢量v0,v1,v2,…,vn-1，获取所述bezier曲线的表达式。

进一步地，所述步骤s1中，所述bezier曲线的初始矢量v0的长度为任意长度，即满足：

||v0||＞0

其中，符号“||||”表示矢量的长度。

进一步地，所述步骤s2中，所述bezier曲线的尺度系数s和旋转角度θ满足以下条件：

s*cosθ≥1

当s*cosθ≥1时，曲率为单调下降函数，即所述bezier曲线为曲率单调下降的n次bezier曲线；其中p(t)为所述bezier曲线的表达式，p'(t)表示p(t)的一阶导矢曲线，p”(t)表示p(t)的二阶导矢曲线，||||表示矢量的长度。

进一步地，所述步骤s2中，所述bezier曲线的尺度系数s和旋转角度θ满足以下条件：

s≤cosθ

同理，当s≤cosθ时，曲率κ(t)为单调上升函数，即p(t)为曲率单调上升的n次bezier曲线。

进一步地，所述步骤s3中，所述bezier曲线对应的矢量v1,v2,…,vn-1的具体表达式为：

vi+1＝s·r·vi，i＝0,1,…,n-2(1)

其中，r为具有旋转角度θ的旋转矩阵。

进一步地，所述步骤s4中，所述bezier曲线的表达式，记为p(t)：

其中，bi(i＝0,1,2,…,n)为所述bezier曲线的控制顶点，且满足bibi+1＝vi；bi,n(i＝0,1,2,…,n)为bernstein基函数。

本发明的有益效果：

本发明通过设定尺度系数和旋转角度，克服了传统方法中高次bezier曲线设计中难以满足曲率单调变化的条件，实现了曲率单调变化的任意次bezier曲线的设计方法。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

图1是根据本发明的曲率单调变化的任意次bezier曲线的设计示意图；

图2是根据本发明的曲率单调变化的任意次bezier曲线的设计方法的流程图；

图3是根据本发明的曲率单调下降的三次bezier曲线的设计示意图；

图4是根据本发明的曲率单调下降的三次bezier曲线的曲率图；

图5是根据本发明的曲率单调上升的四次bezier曲线的设计示意图；

图6是根据本发明的曲率单调上升的四次bezier曲线的曲率图；

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员所获得的所有其他实施例，都属于本发明保护的范围。

图1给出了本发明的曲率单调变化的任意次bezier曲线的设计示意图，图1中控制顶点bi(i＝0,1,2,…,n)可由vi得到，满足bibi+1＝vi，矢量vi和矢量vi+1的长度满足s||vi||＝||vi+1||，因此，在bezier曲线的尺度系数s和旋转角度θ给定的情况下，bezier曲线对应的矢量vi+1，可以由前一个矢量vi通过长度伸缩s倍和角度旋转θ度得到。

实施例一：

参见图2和图3，设计曲率单调下降的三次bezier曲线，即n＝3。

(1)选取初始矢量v0，则控制顶点b0b1＝v0；

(2)选取bezier曲线的尺度系数s＝2和旋转角度θ＝π/3，且s和θ的关系为：s*cosθ＝2*0.5＝1，满足s*cosθ≥1的条件；

(3)根据公式(1)求得

(4)根据v1、v2的表达式及bernstein基函数，利用公式(2)，获取bezier曲线的表达式p(t)，从而绘制出曲率单调下降的三次bezier曲线，其对应的曲率图如图4所示。

实施例二：

参见图2和图5，设计曲率单调上升的四次bezier曲线，即n＝4。

(1)选取初始矢量v0，则控制顶点b0b1＝v0；

(2)选取bezier曲线的尺度系数s＝0.6和旋转角度θ＝π/4，且s和θ的关系为：满足s≤cosθ的条件；

(3)根据公式(1)求得

(4)根据v1、v2、v3的表达式及bernstein基函数，利用公式(2)，获取bezier曲线的表达式p(t)，从而绘制出曲率单调下降的四次bezier曲线，其对应的曲率图如图6所示。

需要特别说明的是，本发明目的在于提供一种基于曲率单调变化的任意次bezier曲线的设计方法，不限于曲率单调下降的三次bezier曲线或曲率单调上升的四次bezier曲线，基于曲率单调上升或单调下降的任意次bezier曲线都适用于本方法。

以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。