一种复杂产品的装配任务规划方法与流程

本发明专利涉及产品装配线工艺规划领域，尤其涉及到一种复杂产品的装配任务规划方法。

背景技术：

目前，复杂产品装配的装配工艺规划和装配任务分配，生产厂商多有根据样品装配试验来进行的装配规划，不但工作量巨大，耗时长，而且工艺设计质量不稳定，设计结果常因人而异，在装配任务划分与分配等方面难以达到理想的效果。为便于实现数字化工厂和管理需求，研究人员应用面向装配线平衡的装配任务分配，在满足产品零部件装配关系约束条件下，结合装配生产实际资源约束情况，依据装配区域内装配节点时间进行装配工艺规划和装配任务分配，保证装配线平衡和装配的顺利进行；

以上装配工艺规划技术，对于传统批量生产装配的单一材料品种的装配工艺规划，由于装配操作的复杂性不高，装配线设置简单，装配任务量的大小基本可以通过装配时间长短衡量，或可以依据样品装配试验进行装配任务分配。而对于复杂装配体，尤其是满足智能制造和个性化需求的制造，装配零部件的多样性和装配的不确定性增加，从而使装配操作的复杂性和装配的易错率增加，装配的复杂性增加，增加的复杂性与装配的难易程度及装配时间直接关联。因而，现有装配工艺规划和装配任务分配技术应用复杂产品的装配任务规划具有明显的局限性。

技术实现要素：

本发明的目的是提供一种更有效适用于个性化和不确定性增加的复杂产品装配线的装配任务规划方法。

本发明为解决其技术问题所采用的技术方案是：

一种复杂产品的装配任务规划方法，包括复杂性来源分析、复杂性的分类描述与度量、建立装配任务规划模型和算法优化求解四个步骤，其特征在于：

(1)所述复杂性来源分析是依据复杂装配体的装配特征，并结合零部件材料、工艺、装配资源及产量规模等信息，分析复杂产品装配的复杂性来源；

(2)所述复杂性的分类描述与度量是从产品零部件复杂性、装配工艺、装配资源、及装配操作复杂性等方面进行装配复杂性的分类描述，并基于装配零部件材料等不同品种零部件对应的装配工艺、装配资源等都是特定的类别或组别，装配工艺、装配资源的装配操作选择及执行为非独立相关的，在一定条件下的装配操作，需要根据对应的条件，建立基于装配条件的条件熵的度量；

(3)所述建立装配任务规划模型是基于复杂性分析的装配任务规划模型，将装配人员作为待分配的背包，装配操作各复杂性的倒数作为待分配任务分配与否的满意度，建立装配系统总复杂性最小的装配任务分配模型；

(4)所述算法优化求解是根据算法搜索得到复杂性最小的装配任务分配，并结合装配现场条件建立的约束来实现装配任务规划问题的求解。

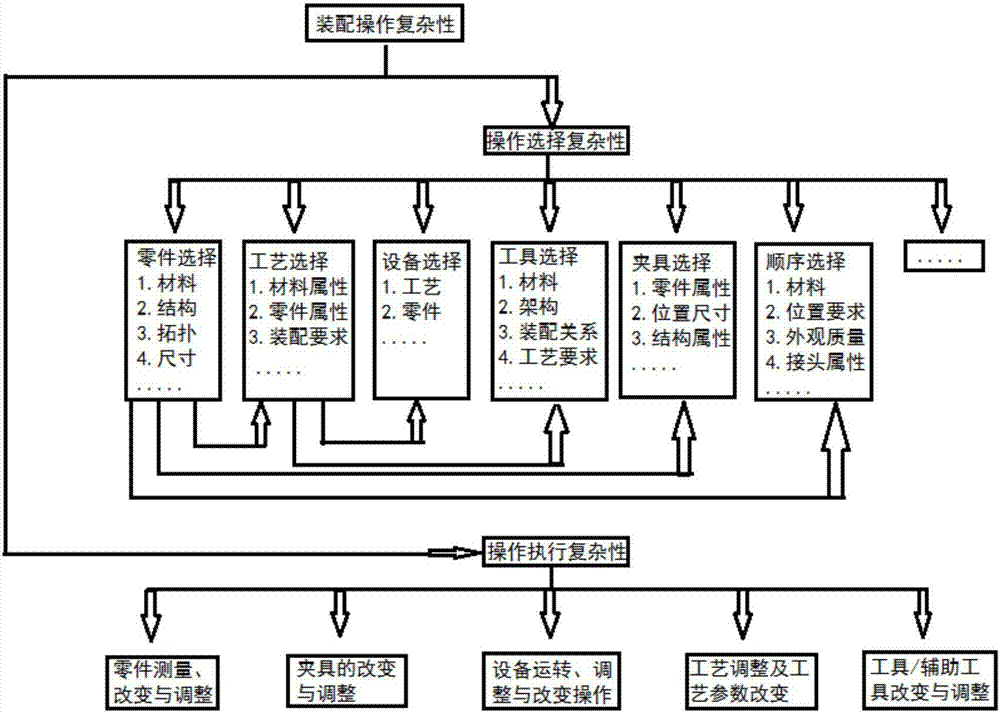
所述复杂性来源分析包括操作选择复杂性c^oc、操作执行复杂性c^op，所述操作选择复杂性包括零件选择、工艺选择、装配设备选择、装配工具选择、装配夹具选择和装配顺序选择六个分析方面，操作执行复杂性包括零件的定位和测量、夹具的改变与调整、设备的操作与调整、工艺调整及参数改变、辅助工具的改变与调整。

所述复杂性来源分析具体表示为：

其中，为第类装配操作选择的作用系数，为第kpv类装配操作执行的作用系数，若装配操作过程中包括第kcu类装配操作选择，则令否则若存在第kpv类装配操作执行行为，则否则为第kcu类装配操作选择信息熵的权重系数，为第kpv类装配操作执行复杂性的权重系数，和分别表示第kpv类装配操作选择复杂性和第kcu类装配操作执行复杂性。

所述算法优化求解具体如下：

(1)目标函数：

假设存在m个装配操作工人mj，n个复杂产品零部件的装配操作任务，装配任务i(i＝1,2,…,n)的第k类装配操作分配给装配任务j的复杂性表示为，将装配零部件i的第k类装配操作任务分配给装配操作工人j的任务分配的价值满意度为对应为复杂性度量的倒数，即:

其中约束条件：

①配给单个操作工人mj的装配任务复杂性不超过

∑c^oc+∑c^op/n，即：

②比较各操作工人任务量的复杂性度量是否与∑c^oc+∑c^op/n近似，即：

(2)编码形式与适应度函数：

①遗传编码：

采用二进制编码方式将复杂产品装配任务分配问题的解空间映射成基因位。用x(m*n)与x(n*k)的两级分层矩阵表示遗传编码，表示零部件i的装配包含的第k类装配操作的作用系数；

②适应度函数表示为：

其中，oj(c)为装配人员j分配任务的目标函数，pj(c)为装配工人j的复杂性超出约束条件的惩罚函数，di(c)为装配任务k隶属于多个背包的惩罚函数，各函数的构造分别为：

其中，λ和γ为惩罚系数，为装配任务i的第k类装配操作分配给装配工人j的复杂性表示，为第i个零件装配的第k类装配操作任务是否分配给第j个装配工人的判断系数；

(3)遗传算子：

遗传算子由选择、交叉和变异三个算子构成，具体实现策略如下：

①选择：采用按正比于适应值的轮盘赌方式进行随机选择，在选择轮盘赌的时候，用折半搜索的方法有效地减少比较次数，确保对应的轮盘在o(log2n)内找到，所述n为种群大小；

②交叉：以矩阵的方式存在的遗传编码方式基因位，在交叉操作中等效为一个长度为m*n*k的编码串，采用一致交叉算子，编码串上的每一位按相同概率进行随机均匀交叉；

③变异：先从群体中的个体编码串中随机挑选一个或者多个基因位，然后按照变异概率pm进行变异，即将当前基因的值取非值。

本发明的优点在于：

1.本发明专利克服现有装配任务规划技术的局限，考虑个性化和智能化需求增加的多样化和不确定性对装配操作的影响，进行装配复杂性分类描述与测量，并建立基于复杂性测度的装配系统复杂性最小的装配任务分配优化模型，通过智能优化算法启发式搜索得到复杂性最小的装配任务分配；

2.该方法通过装配节点复杂性反映复杂产品装配任务难易程度和装配易错率问题，更符合复杂产品装配生产实际，提高复杂产品装配任务规划的自动化水平，提高复杂产品装配规划的效率，减少出错率，更好地保障装配的质量，降低装配成本，缩短生产周期；

3.该方法可用于诸多复杂产品装配体，如多材料轻量化车身、飞机等多样化和智能化需求高的大型复杂装配的任务规划问题。

附图说明

图1是本发明提出的一种复杂产品的装配任务规划方法的流程示意图；

图2是该方法中操作选择复杂性与操作执行复杂性的分类示意图。

具体实施方式

为了使本发明实现的技术手段、创作特征、达成目的与功效易于明白了解，下面结合图示与具体实施例，进一步阐述本发明。

如图1、图2所示，本发明提出的一种复杂产品的装配任务规划方法包括复杂性来源分析、复杂性的分类描述与度量、建立装配任务规划模型和算法优化求解四个步骤：

(1)所述复杂性来源分析是依据复杂装配体的装配特征，并结合零部件材料、工艺、装配资源及产量规模等信息，分析复杂产品装配的复杂性来源；

(2)所述复杂性的分类描述与度量是从产品零部件复杂性、装配工艺、装配资源、及装配操作复杂性等方面进行装配复杂性的分类描述，并基于装配零部件材料等不同品种零部件对应的装配工艺、装配资源等都是特定的类别或组别，装配工艺、装配资源的装配操作选择及执行为非独立相关的，在一定条件下的装配操作，需要根据对应的条件，建立基于装配条件的条件熵的度量；

(3)所述建立装配任务规划模型是基于复杂性分析的装配任务规划模型，将装配人员作为待分配的背包，装配操作各复杂性的倒数作为待分配任务分配与否的满意度，建立装配系统总复杂性最小的装配任务分配模型；

(4)所述算法优化求解是根据算法搜索得到复杂性最小的装配任务分配，并结合装配现场条件建立的约束来实现装配任务规划问题的求解。

装配操作复杂性c^oc，零件选择为实现复杂产品装配的首要选择，建立其复杂性可由对应零件选择的信息熵度量，如式(a)；由于复杂产品装配操作选择的非独立相关性，由图1可见，工艺选择为零件选择下的条件选择，其复杂性可由对应零件选择的条件熵度量，如式(b)所示；同样，设备和工具的选择均为装配工艺选择下的条件选择，对应装配设备选择条件熵和装配工具选择条件熵可分别表示为式(c)和(d)；而装配夹具和装配顺序的选择，为对应零件选择下的条件选择，其复杂性可分别表示为夹具选择条件熵和装配工具选择条件熵如式(e)和(f)；

(a)(b)

(c)(d)

(e)(f)

装配操作执行复杂性c^op，依照装配操作执行对象主要包括：零件的定位、测量及调整过程中产生的操作执行复杂性装配资源的设置、改变与调整过程中的操作执行复杂性具体包括设备改变、调试与调整复杂性工具与辅助工具的操作执行复杂性以及夹具的安装、定位、调整与改变的操作执行复杂性等，装配操作执行复杂性的描述与度量，由各类装配操作执行复杂性的叠加实现；所述复杂性来源分析包括操作选择复杂性c^oc、操作执行复杂性c^op，所述操作选择复杂性包括零件选择、工艺选择、装配设备选择、装配工具选择、装配夹具选择和装配顺序选择六个分析方面，操作执行复杂性包括零件的定位和测量、夹具的改变与调整、设备的操作与调整、工艺调整及参数改变、辅助工具的改变与调整。装配操作复杂性co，由装配操作选择复杂性c^oc与装配操作执行复杂性c^op共同决定。假定用kcu(kcu＝kc1,kc2,...,kc)为各类装配操作选择进行编号，kpv(kpv＝kp1,kp2,...,kp)为各类装配操作执行复杂性编号，并考虑各类操作复杂性影响权重的不同。

所述复杂性来源分析具体表示为：

其中，为第类装配操作选择的作用系数，为第kpv类装配操作执行的作用系数，若装配操作过程中包括第kcu类装配操作选择，则令否则若存在第kpv类装配操作执行行为，则否则为第kcu类装配操作选择信息熵的权重系数，为第kpv类装配操作执行复杂性的权重系数，和分别表示第kpv类装配操作选择复杂性和第kcu类装配操作执行复杂性。

建立基于装配操作复杂性优化的复杂产品装配任务规划模型：

由于装配复杂性与装配的难易程度及其错误率都直接相关，装配复杂性作为装配任务分配的满意度为复杂性越小越优的目标。装配任务分配的目标是使所有人员完成所分配任务复杂性cj＝{c1,c2,...,cm}(j为装配人员数量，j＝1,2,…,m)的最大值最小，即：

cj＝min{max{cj}}＝min{max{c1,c2,...,cm}}；

假设有m个装配人员mj(m1,m2,…,mm)，n个零部件pi(p1,p2,…,pn)的装配任务分配，其中每个零部件的装配包含k(k＝1,2,…,k)类装配操作选择和装配操作执行任务的复杂性；

用(m×n)和(n×k)的两级矩阵表示装配零部件与装配人员之间的关系，复杂产品装配任务的复杂性矩阵可通过c(m*n)与c(n*k)的两级分层矩阵表示，将装配零部件i的第k类装配操作任务分配给操作人员j得到的复杂性表示为其值愈小任务分配的代价愈大，获得的价值满意度愈大。

假定装配零部件i需要完成k(k＝1,2,…,k)类装配操作任务(包括装配操作选择和装配操作执行)，则装配零部件i的装配任务复杂性可表示为(k＝1,2,…,k)。cj(j＝1,2,…,m)为分配给操作人员j的装配任务复杂性，为约定的每位操作人员可承受的最大复杂性；为将第i(i＝1,2,…,n)个零部件的第k类(k＝1,2,…,k)装配操作任务分配给第j(j＝1,2,…,m)位操作人员实现的复杂性。然后，依据装配实际工艺设计及现场要求，确定车门各零部件装配任务的分解。后根据装配人员和装配设备的工作区域约束，首先对装配任务进行初步任务分组，在此基础上进行公共区域的装配任务分配。装配现场的实际情况，装配任务可分配由某一装配人员单独实现零部件的装配，也可根据需要分配至两名装配人员共同实现装配操作。

建立多材料车门装配任务分配问题的目标函数：

(ii)f∈r(mj),j＝1,2,…,m；

(iii)r(g)∈φy,i＝1,2,…,n；k＝1,2,…,k；

(iv)s(g)∈φx,i＝1,2,…,n；k＝1,2,…,k；

(v)p(g)∈φp,i＝1,2,…,n；k＝1,2,…,k；

(vi)c(mj)＝∑c^oc+∑c^op,j＝1,2,…,m；

其中，f为启发式智能优化算法，f为装配任务分配问题，(i＝1,2,…,n；k＝1,2,…,k)为待分配零部件i的第k类装配操作复杂性；为任务分组，由工艺员根据复杂产品装配现场条件实现。mj为装配人员(j＝1,2,…,m)，φz为装配任务在装配群中的位置(位置紧密性)，φp为依照装配工艺类型进行的装配任务分组：

c(mj)＝∑c^oc+∑c^op为每位装配人员的装配操作复杂性；r(g)为依据零部件群所处的位置是内框或外框来分配任务；s(g)为依据零部件群所处的位置是水平或者垂直来分配任务；p(g)为依据装配工艺类型进行的任务分组；为决策变量，若表示装配任务i的第k类装配操作分配给操作人员j，表示不分配；

约束条件(i)表示为所有装配零部件连接点按照连接点群的位置(水平或垂直)、排列紧密性、区域方位及装配工艺等因素进行分组，减少目标的数量；约束条件(ii)表示在任务分配时须考虑操作人员或设备的工艺范围；约束条件(iii)表示任务分配时，尽量将车门装配同一位置侧的任务分配给同一人员；约束条件(iv)表示任务分配时，尽量将车门装配同一类型位置(水平或者垂直)的任务分配给同一人员；约束条件(v)表示，装配工艺类型相同或所用设备相同的装配任务，尽量分配给同一人员；约束条件(vi)为分配装配复杂性计算方法；约束条件(vii)为决策变量的取值范围。

所述算法优化求解具体如下：

(1)目标函数：

假设存在m个装配操作工人mj，n个复杂产品零部件的装配操作任务，装配任务i(i＝1,2,…,n)的第k类装配操作分配给装配任务j的复杂性表示为，将装配零部件i的第k类装配操作任务分配给装配操作工人j的任务分配的价值满意度为对应为复杂性度量的倒数，即:

其中约束条件：

①给单个操作工人mj的装配任务复杂性不超过

∑c^oc+∑c^op/n，即：

②比较各操作工人任务量的复杂性度量是否与∑c^oc+∑c^op/n近似，即：

(2)编码形式与适应度函数：

①遗传编码：

采用二进制编码方式将复杂产品装配任务分配问题的解空间映射成基因位。用x(m*n)与x(n*k)的两级分层矩阵表示遗传编码，表示零部件i的装配包含的第k类装配操作的作用系数；

③适应度函数表示为：

其中，oj(c)为装配人员j分配任务的目标函数，pj(c)为装配工人j的复杂性超出约束条件的惩罚函数，di(c)为装配任务k隶属于多个背包的惩罚函数，各函数的构造分别为：

其中，λ和γ为惩罚系数，为装配任务i的第k类装配操作分配给装配工人j的复杂性表示，为第i个零件装配的第k类装配操作任务是否分配给第j个装配工人的判断系数；

(3)遗传算子：

遗传算子由选择、交叉和变异三个算子构成，具体实现策略如下：

①选择：采用按正比于适应值的轮盘赌方式进行随机选择，在选择轮盘赌的时候，用折半搜索的方法有效地减少比较次数，确保对应的轮盘在o(log2n)内找到，所述n为种群大小；

②交叉：以矩阵的方式存在的遗传编码方式基因位，在交叉操作中等效为一个长度为m*n*k的编码串，采用一致交叉算子，编码串上的每一位按相同概率进行随机均匀交叉；

③变异：先从群体中的个体编码串中随机挑选一个或者多个基因位，然后按照变异概率pm进行变异，即将当前基因的值取非值。

以上实施方式只为说明本发明的技术构思及特点，其目的在于让本领域的技术人员了解本发明的内容并加以实施，并不能以此限制本发明的保护范围，凡根据本发明精神实质所做的等效变化或修饰，都应涵盖在本发明的保护范围内。