一种圆台螺旋型能源桩传热计算方法与流程

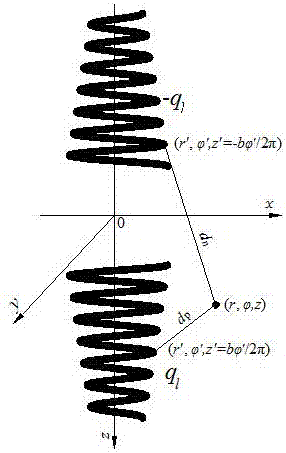
本发明专利涉及一种地源热泵系统地埋管的技术领域，尤其涉及一种能够提高传热效率的空心圆台螺旋型能量桩传热计算，主要适用于建筑供暖供冷的地源热泵技术领域。

背景技术：

地源热泵系统利用地下岩土作为低品位冷热源，由于地下岩土温度较为恒定，且温度范围非常适合热泵机组高效运行，故能有效减少机组运行能耗，为建筑节能减排事业做出积极贡献。地埋管换热器是地源热泵系统最为关键的部件，其换热效率对地埋管系统设计容量及运行效果具有重要影响。单u型、双u型垂直地埋管换热器应用较多，但是其钻孔较深，一般在50m～120m范围，对于南方地区，如重庆、成都等岩石地质区域，钻孔难度大，施工周期长，钻孔费用昂贵，其经济性制约了垂直u型地埋管的推广应用。此外，垂直u型地埋管存在较为严重的钻孔内热短路现象，其换热效率低。近年来，一种能量桩技术得到广泛应用。由于能量桩可以依托建筑基础埋设换热管，大大减少了钻孔费用，其经济性较好。能量桩换热管采用并联双u型、串联双u型及螺旋型布置，提高了传热效率，特别是螺旋型能源桩，大大增加了换热流体与周边岩土的接触面积，其换热效率得到大幅度的提高。相关研究已经表明，螺距是影响螺旋型能量桩传热效率的重要因素，由于螺旋换热管的螺距较小，导致轴向相邻螺旋管之间的存在较为明显的热干扰现象，制约了螺旋型能量桩传热效率的提高。

根据上述问题，我们已经成功申请了中国发明专利“提高传热效率的空心圆台螺旋型能量桩结构”(专利号：201510277399.2申请日：2015-05-27)，该结构能够有效改善热干扰，提高传热效率。本专利针对空心圆台螺旋型能量桩结构，提出其传热过程的计算方法，达到计算速度快、工程设计方便的目标。

在本发明之前，中国发明专利“桩基螺旋埋管在地下水渗流条件下的温度响应计算方法”(公开号：cn106354984a)、“地下水渗流环境下桩埋管换热器的传热计算方法及其验证系统”(公开号：cn106485016a)公开了一种圆柱型螺旋能源桩的传热计算方法，但是该方法不能对圆台型螺旋能源桩进行传热计算，对圆台型螺旋能源桩无法设计、确定一个传热模型，还不能揭示圆台型螺旋能源桩内部传热的规律，也不能得到圆台型螺旋能源桩传热计算的公式。

技术实现要素：

本发明针对现有传热计算方法不能对圆台型螺旋能源桩进行传热计算、不能揭示圆台型螺旋能源桩内部传热的规律、不能得到圆台型螺旋能源桩传热计算的公式等不足，提供一种能够提高传热效率的空心圆台螺旋型能量桩传热计算方法。

一种圆台螺旋型能源桩传热计算方法；其特征在于：采用镜像热源法，假设z＝0表面为对称面，在-z方向，存在与圆台型螺旋线对称的一束螺旋线热汇，发热量为-ql；

根据格林函数法，在无限大均匀介质中，从τ’时刻开始，位于点的单位强度的点热源作用一定时间后，在τ时刻计算点处的土壤温度计算公式如下：

式中，——格林函数；αs——岩土热扩散率，m²/s；r——计算点的径向距离，m；——计算点的周向角，rad；z——计算点的高度，m；

热源螺旋线的几何表达式为：

同理，对于发热量为-ql的螺旋热汇而言，其螺旋线几何表达式为：

根据式(2)及式(3)可知，热源螺旋线上的点到计算点z)的距离dp为：

热汇螺旋线上的点到计算点的距离dn为：

从τ＇＝0时刻开始，在螺旋热源与热汇综合作用下，结合式(4)及式(5)，换热区域点处的温升△t可对热源与热汇沿螺旋线与作用时间进行双重积分得到：

式中，ρ——密度，kg/m³；c——质量比热容，j/(kg.℃)；l1、l2分别——螺旋线起点、终点的位置，m；

对时间τ＇进行积分，令故有：

τ′＝τ-1/(4αsu²)(7)

两边同时微分可得：

dτ′＝1/(2αu³)du(8)

根据式(7)可知，当τ＇＝0时，当τ＇＝τ时，u＝∞，将式(7)及式(8)带入式(6)，整理可得：

式中，λ——导热系数，w/(m.k)；

将螺旋线微元长度dl转换为螺旋线微元角度在笛卡尔坐标系下，根据螺旋线的几何表达式(2)，x、y、z方向的微元长度为：

则，螺旋线微元的长度dl可按下式计算：

令则带入式(9)，整理可得：

令dpu＝xp,dnu＝xn，则上式可变换为：

根据误差函数的性质可知：则上式进一步变换为：

式中，为余误差函数。将式的表达式带入式(14)，可得：

进一步的特征是：对式(15)进行无量纲化，令：θ＝λ△t/ql，hb＝hb/rb，ht＝ht/rb，b＝b/rb，r＝r/rb，z＝z/rb，fo＝ατ/rb²，则式(15)可写为：

式中，

当θ＝0°时，圆台型螺旋能量桩即为圆柱型螺旋能量桩；当θ＝0°时，式(16)转化为：

式中，

相对于现有技术，本发明专利具有如下特点：

1)由于圆台型能量桩铺设与圆台面上，圆台曲面与竖直方向具有一定的角度，可有效降低井壁的坍塌风险。

2)流体刚进入换热管时，顶部流体与岩土的换热温差大，径向热干扰较强，而圆台型螺旋能源桩顶面半径大，可有效缓解径向热干扰现象，提高换热效率。

3)在轴向螺距b相同的情况下，cyhep轴向相邻螺旋管的距离大于cohep，且cohep底部的螺旋半径较小，故cohep底部的相邻螺旋管的距离与螺旋半径的比值较大，可有效降低圆台型能量桩底部相邻螺旋管间的轴向热干扰现象，提高换热效率。

4)能对圆台型螺旋能源桩进行传热计算，能揭示圆台型螺旋能源桩内部传热的规律；提供了一个圆台型螺旋能源桩传热计算的公式等。

5)本发明的计算方法，理论结果数值与实测结果数值吻合程度高，说明本专利的圆台螺旋型能源桩传热计算方法精确度较高。

附图说明

图1是本发明圆台型螺旋能量桩示意图；

图2是本发明镜像热源法示意图；

图3是本发明计算结果准确性的验证图。

具体实施方式

如图1中，本发明专利的圆台型螺旋能量桩示意图，圆台型能量桩的结构特点是螺旋换热管铺设在圆台面下，其螺旋半径随深度的增加而线性降低。圆锥角为θ，z方向螺距为b，相邻螺旋管之间的距离为d，b与d的关系为：b＝d·cosθ，底面半径为rb，顶面半径为rt，rt>rb，顶面距地面距离为ht，底面距地面距离为hb。

该种圆台型螺旋能量桩有如下优势：1)由于圆台型能量桩铺设与圆台面上，圆台曲面与竖直方向具有一定的角度，可有效降低井壁的坍塌风险。2)流体刚进入换热管时，顶部流体与岩土的换热温差大，径向热干扰较强，而圆台型螺旋能源桩顶面半径大，可有效缓解径向热干扰现象，提高换热效率。3)在轴向螺距b相同的情况下，cyhep轴向相邻螺旋管的距离大于cohep，且cohep底部的螺旋半径较小，故cohep底部的相邻螺旋管的距离与螺旋半径的比值较大，可有效降低圆台型能量桩底部相邻螺旋管间的轴向热干扰现象，提高换热效率。

为了探究新型cohep的换热特性，特别是螺旋管外壁温度分布特性，本文将在一定假设条件的基础上，采用格林函数法，推导得出圆台型螺旋能量桩的解析解表达式，并以此为基础，分析讨论圆台型能量桩换热特性。

为了保证在岩土表面z＝0处为第一类边界条件，采用镜像热源法，假设z＝0表面为对称面，在-z方向，存在与本发明圆台型螺旋线对称的一束螺旋线热汇，发热量为-ql，结构如图2所示。

在上述假设条件下，根据格林函数法，在无限大均匀介质中，从τ’时刻开始，位于点的单位强度的点热源作用一定时间后，在τ时刻计算点处的土壤温度计算公式如下：

式中，——格林函数；αs——岩土热扩散率，m²/s；r——计算点的径向距离，m；——计算点的周向角，rad；z——计算点的高度，m。实际上，指数函数中分子项为热源点与计算点的距离的平方。

根据图1所示圆台型螺旋能量桩各参数的描述，热源螺旋线的几何表达式为：

同理，对于发热量为-ql的螺旋热汇而言，其螺旋线几何表达式为：

根据式(2)及式(3)可知，如图2所示，热源螺旋线上的点到计算点的距离dp为：

热汇螺旋线上的点到计算点的距离dn为：

从τ＇＝0时刻开始，在螺旋热源与热汇综合作用下，结合式(4)及式(5)，换热区域点处的温升△t可对热源与热汇沿螺旋线与作用时间进行双重积分得到：

式中，ρ——密度，kg/m³；c——质量比热容，j/(kg.℃)；l1、l2分别——螺旋线起点、终点的位置，m。

为了简化式(6)，首先对时间τ＇进行积分，令故有：

τ′＝τ-1/(4αsu²)(7)

两边同时微分可得：

dτ′＝1/(2αu³)du(8)

根据式(7)可知，当τ＇＝0时，当τ＇＝τ时，u＝∞，将式(7)及式(8)带入式(6)，整理可得：

式中，λ——导热系数，w/(m.k)。

上述表达式为沿螺旋线l进行积分的结果，为了便于计算，下面将螺旋线微元长度dl转换为螺旋线微元角度

在笛卡尔坐标系下，根据螺旋线的几何表达式(2)，x、y、z方向的微元长度为：

则，螺旋线微元的长度dl可按下式计算：

令则带入式(9)，整理可得：

令dpu＝xp,dnu＝xn，则上式可变换为：

根据误差函数的性质可知：则上式进一步变换为：

式中，为余误差函数。将式的表达式带入式(14)，可得：

式(15)即为圆台型能量桩解析解的具体表达式。为了更加方便的对圆台型能量桩进行传热特性分析，下面对式(15)进行无量纲化，令：θ＝λ△t/ql，hb＝hb/rb，ht＝ht/rb，b＝b/rb，r＝r/rb，z＝z/rb，fo＝ατ/rb²，则式(15)可写为：

式中，

实际上，当θ＝0°时，圆台型螺旋能量桩即为圆柱型螺旋能量桩，圆柱型螺旋能量桩是本文提出的圆台型螺旋能量桩的一种特殊情况。当θ＝0°时，式(16)可转化为：

式中，

为了验证本专利所提出的计算方法的正确性，开展了θ＝10°时的实验研究，测试了实验期间螺旋型能源桩的进出口水温，图3给出了理论计算和实测结果随时间的变化曲线，对比可知，理论计算结果与实测结果吻合程度高，说明本专利提出的圆台螺旋型能源桩传热计算方法精确度较高。

最后需要说明的是，本发明的技术方案非限制技术方案，本领域的普通技术人员应当理解，那些对本发明的技术方案进行的修改或者等同替换，而不脱离本技术方案的宗旨和范围，均应涵盖在本发明的权利要求范围当中。