一种汽车车身正向概念设计截面形状优化方法与流程

本发明涉及汽车车身设计领域，特别是车身概念设计阶段结构截面形状设计优化方法。

背景技术：

概念设计是汽车车身设计流程的重要组成部分，逆向概念设计是目前汽车企业广泛采取的设计方式。然而，逆向概念设计往往过度受制于标杆车车型的限制，设计周期长、效率低、质量不高，难以实现性能为主导的车身设计。正向概念设计，在设计之初就考虑车身的重要性能指标，如静态弯曲刚度、扭转刚度和一阶自由振动特征频率，利于实现性能为主导的车身概念设计，提高设计效率，缩短研发周期。

基于近似理论的有限元分析软件是当前车身概念设计主导的设计工具。车身有限元模型往往由壳单元对标杆车的详细车身模型离散而成，设计自由度低，前期出现的问题在后期往往很难修正甚至根本无法修正。且重复的有限元建模效率低，周期长，很难实现性能为主导的整体优化设计。车身主要承载结构为半刚连接的薄壁梁组成的空间框架，多个薄壁梁的截面设计是车身概念设计的一项重要工作。目前，尚未有商业软件用于车身截面设计，车身研发实践中广泛采用基于经验的试凑法，该方法返工量大，耗时严重，可靠性低，无法保证车身整体结构参数最优。因此，研究主断面形状优化的方法，提供相应的软件工具具有重要意义。国内外学者提出的车身截面形状优化方法多是基于有限单元法。这种方法以截面控制点的坐标为优化设计变量，适用于车身某一指定位置截面的分析，当需要优化设计的车身截面多达十几甚至几十个时，就难以奏效。此外，承载薄壁梁的制造和装配性约束因素考虑不周全，导致当前车身截面形状优化方法难以满足车身研发的实际需求。此外，车身研发流程中缺乏可与车身结构分析融为一体的主断面优化应用软件系统，尤其是采用分布式并行计算等先进技术，以协同方式解决车身整体结构动、静态分析和主断面形状设计优化的软件平台还未见报道。因此，急需一种基于精确理论和先进计算方式，可与车身结构分析方法集成使用的车身截面形状优化方法和软件系统。

技术实现要素：

本发明所要解决的技术问题是，针对现有技术不足，提供一种汽车车身正向概念设计截面形状优化方法，提高汽车车身概念设计效率。

为解决上述技术问题，本发明所采用的技术方案是：一种汽车车身正向概念设计截面形状优化方法，包括以下步骤：

1)确定汽车车身简化几何线框模型；

2)根据所述车身简化几何线框模型求取车身薄壁梁、接头力学属性，建立考虑泊松效应的车身薄壁梁单元传递刚度矩阵分析模型；

3)选取一定数量的薄壁梁进行顶层截面形状优化；选取需要考虑截面变化的薄壁梁进行底层截面形状优化。

步骤1)中，所述车身简化几何线框模型为半刚连接的薄壁梁构成的空间框架结构。

步骤2)中，所述车身薄壁梁单元传递刚度矩阵分析模型的纵向振动刚度矩阵表达式如下：

其中，e为杨氏模型，a为车身结构梁单元截面面积，ν为车身材料泊松比，ρ为车身材料密度，ip为车身结构梁单元截面极惯性矩，l为薄壁梁的长度，ω为频率。

步骤3)中，顶层截面形状优化的数学模型如下：

其中，x为顶层截面形状优化的设计变量，m为车身质量，f(x)为车身质量函数；δ为车身竖直方向最大变形，g1(x)为δ关于x的函数；φ为车身纵向扭转角，g2(x)为φ关于x的函数；freq为一阶特征频率；naa为拔模负角总数；nip为车身薄壁梁板件交叉点总数；nii为无效内点总数；δallowable,φallowable,freqallowable分别为δ,φ,freq对应的极限允许值；lb表示顶层截面形状优化设计变量的下边界，ub表示顶层截面形状优化设计变量的上边界。

步骤3)中，底层截面形状优化的数学模型为：

其中，x′为底层截面形状优化的设计变量，m′为车身质量，f′(x′)为车身质量函数；δ′为车身竖直方向最大变形，g′1(x′)为δ′关于x′的函数；φ′为车身纵向扭转角，g′2(x′)为φ′关于x′的函数；freq′为一阶特征频率；n′aa为拔模负角总数；n′ip为车身薄壁梁板件交叉点总数；n′ii为无效内点总数；δ′allowable,φ′allowable,freq′allowable分别为δ′,φ′,freq′对应的极限允许值；lb′表示底层截面形状优化设计变量的下边界，ub′表示底层截面形状优化设计变量的上边界。与现有技术相比，本发明所具有的有益效果为：首先，本发明提出的车身截面优化方法是基于精确理论的传递刚度矩阵法，对于任何梁单元进行静态和动态结构分析时，都无需再细分单元以提高计算精度。再者，目前国内外鲜有学者考虑薄壁梁的泊松效应，本发明推导了考虑泊松效应的改良的动态刚度矩阵。而且，本发明选取比例向量和厚度作为设计变量，每个薄壁梁单元只需要三个优化变量，若采取截面控制点坐标作为设计变量，动辄需要数十个设计变量。本发明的方法有效减少了变量数目，使得多截面优化具有了可行性。此外，本发明提出了三个制造和装配约束条件，使得优化解具有实际可制造性。分布式并行优化技术的使用，大大提高了计算速度，可以解决使用遗传算法求解大规模截面优化问题耗时过长的弊端。

附图说明

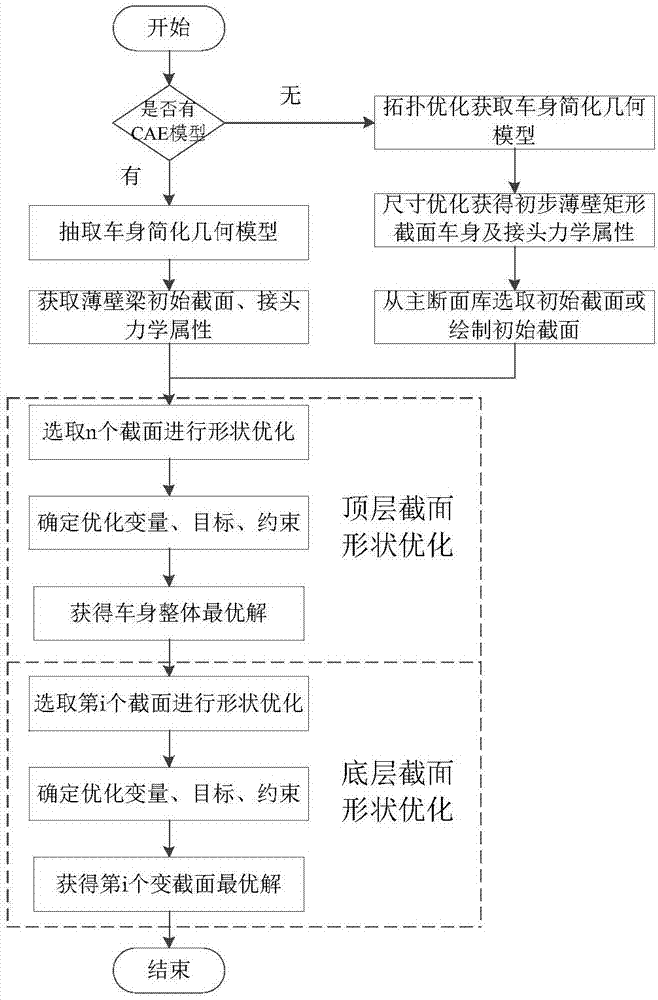
图1是汽车车身正向概念设计自顶向下多截面形状优化设计的实现步骤示意图；

图2是标杆车详细cae模型示意图；

图3是标杆车对应的简化线框模型示意图；

图4是半刚梁单元示意图；

图5是该方法对应的系统示意图；

图6是需要优化截面的位置及初始截面示意图；

图7是一种典型的薄壁梁截面形状示意图；

图8是截面形状关于比例向量法变换的示意图；

图9是三种装配和制造约束示意图；(a)拔模负角；(b)交叉点；(c)无效内点；

图10是车身静态弯曲扭转测试习惯示意图；(a)h点弯曲测试；(b)扭转测试；

图11是顶层截面形状优化适应度函数收敛示意图；

图12是顶层截面形状优化结果示意图；(a)no.1截面；(b)no.2截面；(c)no.3截面；(d)no.4截面；(e)no.5截面；(f)no.6截面；(g)no.7截面；(h)no.8截面；(i)no.9截面；(j)no.10截面；

图13是底层截面形状优化适应度函数收敛示意图；

图14是底层截面形状优化结果示意图；(a)no.1段；(b)no.2段；(c)no.3段；

图15是不同数量截面形状优化后最优质量和计算耗时示意图；

图16是不同并行优化计算加速比示意图。

具体实施方式

步骤1：确定车身简化几何线框模型。如果设计之初存在详细的cae模型，车身简化几何模型可以由详细几何模型抽取而得；如果设计之初没有详细的cae模型，可以建立可以反映车身基本布置的实体模型，然后通过拓扑优化技术获取车身简化几何线框模型。为了方便对标起见，以下步骤均以设计之初存在详细cae模型为例说明。

步骤2：求取薄壁梁、接头力学属性，建立车身传递刚度矩阵分析模型。车身概念模型为半刚连接的薄壁梁组成的空间框架结构，用扭转弹簧模拟实际车身接头柔度。薄壁梁与弹簧力学属性均可以通过详细cae模型提取获得。对概念模型进行结构分析，并与标杆车对标。

步骤3：选取一定数量的薄壁梁进行顶层截面形状优化，薄壁梁初始截面形状由详细cae模型抽取而得。在此阶段，每个薄壁梁均简化为等截面梁单元，设计变量为比例向量和厚度，用三个设计变量便可以控制一个薄壁梁截面形状的变化，与使用控制点坐标的传统方法相比，大大减少了设计变量数目，使得多截面形状优化具有了可行性。

步骤4：选取某一特定薄壁梁进行底层截面形状优化，薄壁梁初始截面形状由步骤3获得。

所述步骤3中，形状优化基于一种可以对框架结构进行精确静力分析、动力分析的传递刚度矩阵法。该方法由刚度矩阵法与传递矩阵法有机构成，可以在使用尽可能少的自由度的情况下，对任意半刚连接空间框架结构进行精确的静态分析和动态分析。与传统的有限单元法不同，传递刚度矩阵法基于结构的实际变形情况建立结构刚度关系方程，是一种精确的解法。并且，考虑到薄壁梁的特性—与厚壁梁相比截面面积往往较小，使用洛夫杆理论重新推导了考虑泊松效用的改良的动态刚度矩阵，进一步提高了计算精度。

所述步骤3中，建立了以比例向量和厚度作为设计变量，以车身精确的静态弯曲刚度、扭转刚度、一阶自由振动特征频率和三个制造装配条件作为约束条件，以车身质量最轻作为目标函数的优化模型。采用遗传算法求解该非线性约束优化问题，为了解决优化计算耗时过长的弊端，应用了分布式并行优化技术，显著提高了计算效率，如使用两台计算机共8核心进行分布式并行计算，可以获得5.46倍的加速比。

所述步骤4中，首先选取需要考虑截面变化的薄壁梁作为优化对象，将该薄壁梁划分为若干段等截面薄壁梁单元。与所述步骤3相比，步骤4还有独特的约束条件，即每段薄壁梁单元截面需具有相似性，且不同段内薄壁梁单元的厚度必须相同，因为它们是由相同钣金件冲压而成。这些都可以根据比例向量法很好控制。另外，对于被重新划分为若干段薄壁梁的优化梁单元使用传递刚度矩阵法，避免了重新对车身模型建模和编码，大大提高分析效率。

下面结合附图1–15，顶层截面形状优化以优化车身侧围截面形状为例，底层截面形状优化以b柱为例，对本发明的具体实施方式进行详细说明。

步骤1：由图2所示的标杆车详细cae模型，抽取图3所示的车身概念设计简化线框模型、图4所示的薄壁梁相关的截面和扭转弹簧力学属性。

步骤2：建立车身传递刚度矩阵分析模型。将车身简化几何模型信息输入本发明开发的系统中分析静态弯曲刚度、扭转刚度、一阶自由振动特征频率，并与标杆车对标。结构静态和动态分析基于本发明者提出的传递刚度矩阵法。其推导的基本过程为：根据梁单元受力的实际变形求取精确的静态、动态刚度矩阵；利用刚度矩阵和传递矩阵相互变换关系和传递矩阵法，推导图4所示半刚薄壁梁的传递矩阵、静态和动态刚度矩阵；将该半刚薄壁梁作为一个超单元代入结构分析。同时，考虑到薄壁梁相对于厚壁梁，截面面积较小，利用洛夫杆理论推导了考虑泊松效应的改良的刚度矩阵。改良的杆动态刚度矩阵为

其中

其中e为杨氏模型，a为截面面积，ν为泊松比，ρ为材料密度，ip为极惯性矩，l为薄壁梁的长度，ω为频率。

步骤3：如图6所示，选取车身侧围进行顶层截面形状优化对象，截面初始形状由cae模型抽取获得。车身典型的薄壁梁截面如图7所示，由若干板件冲压焊接而成，每个板件的截面可视为由若干矩形段构成，从而计算截面几何属性。如图7，截面控制点分为两类，即可动点和固定点。其中，固定点在优化过程中保持不变，可动点在设计过程中可以根据对应的比例向量进行坐标转换，如图8所示。

图9所示为三个制造与装配约束。薄壁梁由若干板件冲压焊接而成，因此，图9的(a)中的拔模负角是不允许出现的；焊接时，任意两块板件不允许交叉，图9的(b)中的交叉点是不允许出现的；折边被某一腔包围也是不允许出现，即图9的(c)所示。

定义设计变量向量为

x＝[θ,sv,t](3)

其中

n为优化截面总数。

顶层截面形状优化的数学模型为

其中，m为车身质量；δ为竖直方向最大变形，如图10的(a)所示；φ为扭转角，如图10的(b)所示；freq为一阶特征频率；naa为拔模负角总数；nip为交叉点总数；nii为无效内点总数；δallowable,φallowable,freqallowable分别为δ,φ,freq对应的极限允许值，由对标实验获得，分别取0.8250,0.1910°，26.6000hz。采用惩罚函数法处理公式(5)中的六个约束。

顶层形状优化中设计变量的边界值、最优值如表1所示，其中lb表示下边界，ub表示上边界。适应度函数收敛情况如图11所示，优化后截面如图12所示，顶层截面形状优化前后车身性能对比如表2所示。

表1顶层形状优化中设计变量的边界和最优值

表2顶层形状优化前后车身性能对比

步骤4：选取b柱上半部分，即图6中第10号薄壁梁进行底层截面形状优化。在本算例中，将该薄壁梁划分为三个等截面薄壁梁单元。与所述步骤3相比，步骤4还有独特的约束条件，即每个薄壁梁单元截面需具有相似性，且不同阶薄壁单元的厚度必须相同，因为它们是由相同钣金件冲压而成。这些都可以根据比例向量法很好控制。另外，对于被重新划分为若干薄壁梁的优化梁单元使用传递刚度矩阵法，避免了重新对车身模型建模和编码，显著提高分析效率。

定义设计变量向量为

x′＝[θ′,sv′,t′](6)

其中，

优化数学模型为

顶层形状优化中设计变量的边界值、最优值如表3所示。适应度函数收敛情况如图13所示，优化后截面如图14所示，顶层截面形状优化前后车身性能对比如表4所示。

表3底层截面形状优化设计变量的边界和最优值

表4底层截面形状优化前后车身性能对比

在步骤3和步骤4中，如图15所示，在顶层截面形状优化中，随着优化截面的增加，车身轻量化效果越来越好，但是，计算耗时也急剧增加。步骤2中的顶层截面形状优化，约耗时2600秒。为了加速优化计算，本发明提出了利用matlab并行工具箱和分布式计算服务器进行分布式并行优化技术。计算加速比如图16所示，在两台计算机上使用2n(n＝1–4)核心进行分布式任务并行计算时，可以获得1.86–5.46倍的加速比，显著提高了优化计算效率。