一种复杂多源异构数据同化方法与流程

技术特征：

1.一种复杂多源异构数据同化方法，其特征在于：包括如下步骤：

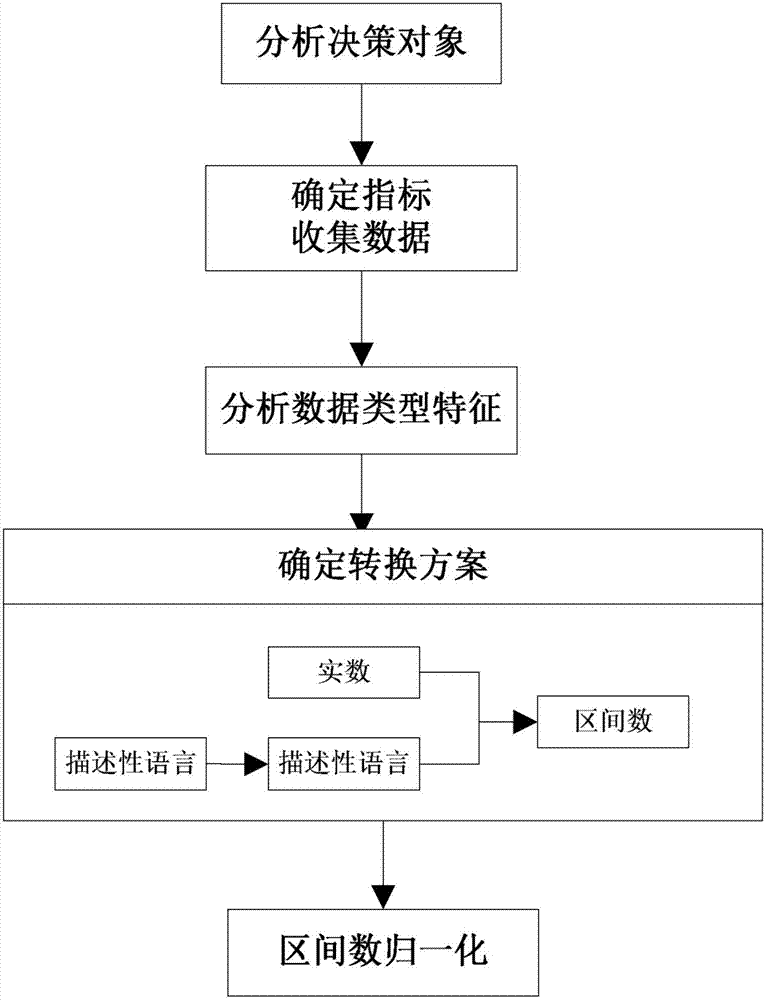
一、收集决策数据信息，并分析所述决策数据信息的数据类型特征；

二、将所述数据类型特征中的描述性语言用直觉模糊集的形式表示出来，并与所述数据类型特征中的实数分别转化为区间数；

三、将所述区间数进行归一化处理。

2.根据权利要求1所述的一种复杂多源异构数据同化方法，其特征在于，在步骤二中，将所述数据类型特征中的描述性语言用直觉模糊集的形式表示出来的步骤具体为：

定义设X是一个非空集合，称F是一个直觉模糊集：

F＝{<x，uF(x)，vF(x)>|x∈X}，

其中，0≤uF(x)+vF(x)≤1，uF：X→[0，1]，vF：X→[0，1]；uF(x)和vF(x)分别称为元素x对集合F的隶属度和非隶属度，πF(x)＝1-uF(x)-vF(x)是元素x对集合F的犹豫度，即不确定性度。

3.根据权利要求2所述的一种复杂多源异构数据同化方法，其特征在于，在步骤二中，将所述数据类型特征中的描述性语言用直觉模糊集的形式表示出来，并与所述数据类型特征中的实数分别转化为区间数的步骤具体为：

一、定义区间数：

定义区间数为a，则

a＝[a^D,a^G]

其中，a^D、a^G均为实数，且a^D≤a^G，特别地，当a^D＝a^G时，则区间数a指的是实数；

二、将实数转换为区间数：

实数r可以表示为区间数r＝[r,r]；

三、将直觉模糊数转换为区间数：

记直觉模糊数为a＝[a^L，a^M，a^U]其中，a^L、a^M、a^U均为实数，且a^L＜a^M＜a^U，则其隶属度函数表示为：

可得直觉模糊数a的左右隶属度分别为

和

则求得左右期望分别为：

和

则根据上式可以将直觉模糊数转化为区间数表示为

4.根据权利要求3所述的一种复杂多源异构数据同化方法，其特征在于，如果两个区间数a＝[a^D,a^G]和b＝[b^D,b^G]，定义区间数a和b之间的距离为：

其中，P为≥2的正整数；

相对应地，两个直觉模糊数a＝[a^L，a^M，a^U]b＝[b^L，b^M，b^U]之间的距离表示为：

5.根据权利要求1所述的一种复杂多源异构数据同化方法，其特征在于，决策模型的决策指标的属性类型为效益型和成本型，采用极差变换法，依据效益型指标和成本型指标的规范化方法，分别对决策指标进行归一化处理；则步骤三中将所述区间数进行归一化处理的步骤具体为：记决策指标值为区间模糊规范后记为

规范化的方法是：

和

其中，I1和I2分别表示效益型指标和成本型指标的下标集。