一种基于多次编码重投影的深度回声状态网络模型构建方法与流程

本发明涉及储备池计算及神经网络研究技术领域，具体涉及一种基于多次编码重投影的深度回声状态网络模型构建方法。

背景技术：

近年来，有许多层次化的循环神经网络框架被相继提出。然而，这些层次化的循环神经网络的学习效率并不高，并且依赖于时间方向上梯度反向传播算法，如何提出一种层次化循环神经网络的高效学习算法至今仍是一个棘手的问题。储备池计算模型是循环神经网络的一种，由于其不必学习递归连接权重，学习方法简单高效，在近十年来受到极大的关注，已被广泛用于混沌时间序列建模、动态系统控制等领域。但是目前的主流储备池计算架构仍局限于单个隐含层的网络结构，这种结构无法像层次化循环神经网络那样捕捉时间序列中的多尺度结构。因此，如何建立一个高效的层次化深度回声状态网络模型，实现对该深度神经网络的训练是一个值得研究的重要问题。

在训练基于层次化回声状态网络的模型时，一个很关键的问题是如何在这个分层系统中发挥储备池计算架构中高效学习的优势，而不仅仅是简单的拼接多个储备池来构造层次化系统。第一个对层次化回声状态网络模型的尝试是2007年Jaeger所提出的DFD模型。其核心思想是堆叠式地构造层次化储备池网络，低层次的网络为高层次网络的输出提供权值，通过梯度学习来学习这个权值和每层网络的输出来获得各层次的多尺度特征。虽然该层次化模型是基于储备池构造的，但是它抛弃了储备池高效的学习机制，相比于原始回声状态网络中的线性回归，其训练计算复杂度大大增加。随后，Triefenbach等人同样构造了级联的回声状态网络来获取多尺度语音状态，并将隐马尔可夫模型作为音素语言模型用于音素识别任务，该架构逐层需要不同监督信息来训练一个单层的储备池，其本质上并不是一个层次化的储备池计算方法。最近，一种多层次回声状态机被Z.K.Malik等人提出，其各个层次的储备池规模相同，内部权重矩阵和储备池间的权重矩阵均是随机生成，且都要求矩阵的谱半径小于1。然而，这种模型并没有充分发挥储备池高维投影的能力，本质上相当于多次的状态转移，在实验中并没有发现应有的多尺度特性。后来，C.Gallicchio等人提出一种层次化储备池模型，与多层次回声状态机相似,其储备池也是有随机生成的权重矩阵，但没有储备池大小相等的限制，并且将输入引入到了每层的储备池。但是该架构仍然存在不足，主要原因在于其多层次特征的结论依赖于输入到各层的连接，如果缺少这些连接，发现这种层次化结构也同样不能带来多尺度特征，由此可见，直接叠加多个储备池还不能有效地建立起一个高效的层次化回声状态网络模型。因此，如何构建一个高效的层次化回声状态网络模型，使其充分发挥传统储备池的特性并捕捉动态系统的多尺度特征是当前亟待解决的一个问题。

技术实现要素：

本发明的目的是为了解决现有技术中的上述缺陷，提供一种基于多次编码重投影的深度回声状态网络模型构建方法，在传统的层次化回声状态网络中引入多重的投影层与编码层，对输入时间序列进行高维投影及低维映射交替循环操作，实现对多尺度动态系统中时间序列的精准预测及多尺度动态特征的捕捉，是一种新型的深度编码储备池计算框架。该深度回声状态网络模型能够通过交替地使用无监督编码技术和储备池高维投影技术实现对时间序列中的多尺度信息进行高效建模。

本发明的目的可以通过采取如下技术方案达到：

一种基于多次编码重投影的深度回声状态网络模型构建方法，所述的构建方法包括下列步骤：

S1、网络初始化，确定储备池的层数K，K>1及初始化储备池的内部参数，内部参数包括储备池规模N，稀疏度α，谱半径SR、输入尺度IS以及遗忘率γ，根据内部参数生成投影矩阵和储备池内部递归矩阵，选取一种非监督的降维编码器并设置编码器的编码器维度；

S2、信号输入，输入初始信号u，令U ⁱ＝u，其中，Uⁱ表示第i层储备池的输入信号，当i＝1时即为初始信号；

S3、状态更新，将Uⁱ作为输入信号输入到第i层储备池中，实现将Uⁱ投影到高维的回声状态空间中，得到输出信号在i层储备池中的所有时刻上的回声状态

S4、循环条件判断，如果i＜K，K为储备池的层数，进入步骤S5，否则，进入步骤S7；

S5、降维编码，将第i号储备池中的回声状态作为第i层编码器的输入信息，进行降维压缩，得到编码器的特征表示其中，表示紧随第i层储备池之后编码器的特征表示；

S6、循环操作，令作为下一个储备池的输入信息，即令第i层储备池的输入信号i＝i+1；返回步骤S2；

S7、模型求解，将直接连接信息u、编码器的特征表示及输出层的信息收集到矩阵M中，并通过线性回归技术学习相应的连接权值，将教师信号收集至矩阵T中，通过引入Tikhonov正则化项,构建岭回归问题实现对深度编码回声状态网络模型最优权重矩阵W^out的求解。

进一步地，引入非监督编码器如主成分分析法对储备池中回声状态进行压缩编码，并将每个编码层的输出信息流连接到输出层，实现对时间序列多尺度动态特征的捕捉。

本发明相对于现有技术具有如下的优点及效果：

本发明通过引入投影及无监督编码的交替操作，建立起一个新型高效的编码重投影回声状态网络。当一个输入时间序列被投影到储备池中，获得相应的高维回声状态时，位于储备池之后的编码层能够将这些回声状态信息表示编码到一个低维的空间。这些低维的表示信息随后又被另一个回声状态网络处理。通过在这个层次化框架中交替使用投影层和编码层，这个深度回声状态网络能够充分利用传统回声状态网络中时序核的特性去探索时间序列的多尺度动态结构，在混沌系统的时间序列预测中相比于其他层次储备池计算模型表现出更优的性能，且其在时间复杂度上保持了传统的回声状态网络的高效计算的特点。

附图说明

图1是本发明基于多次编码重投影的深度回声状态网络架构图；

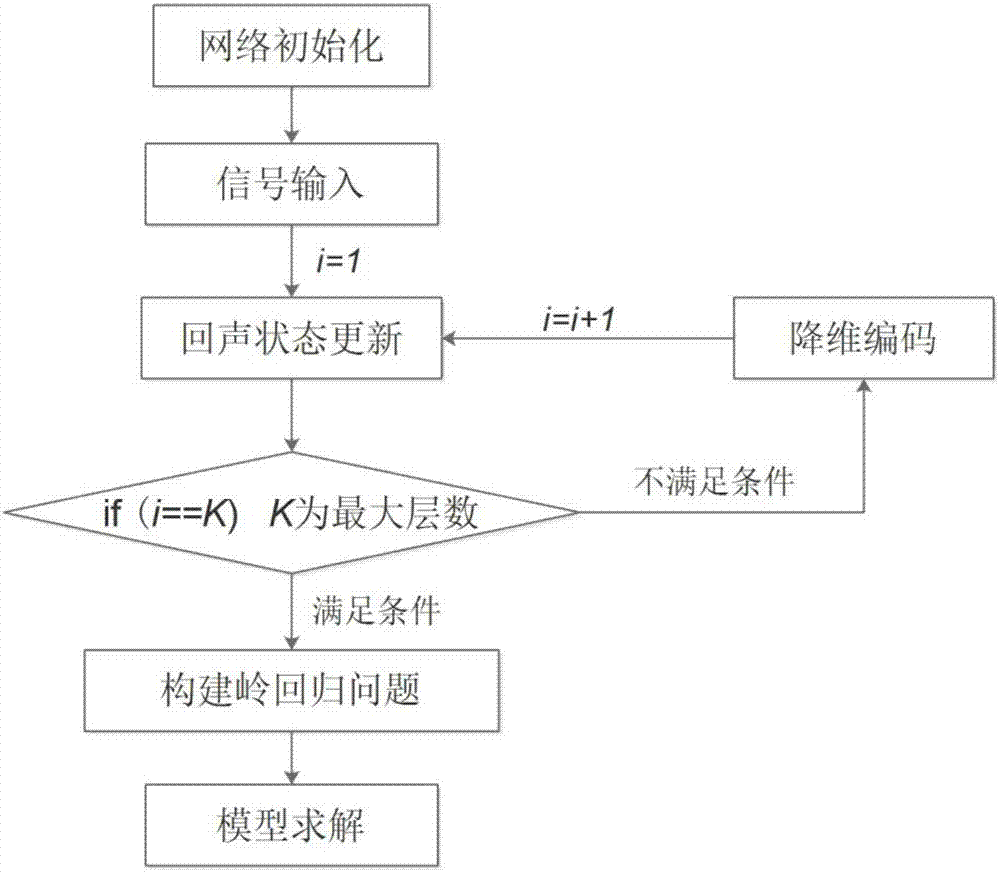
图2是本发明基于多次编码重投影的深度回声状态网络模型的构建流程图。

具体实施方式

为使本发明实施例的目的、技术方案和优点更加清楚，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

实施例

如图1和图2所示，图1为本发明基于多次编码重投影的深度回声状态网络架构图，图2为本发明基于多次编码重投影的深度回声状态网络模型的构建流程图，本实施例提出一种用于捕捉混沌系统多尺度动态特性的深度回声状态网络模型，该模型是适用于混沌时间序列建模的预测模型及层次化储备池计算框架。

基于多次编码重投影的深度回声状态网络模型的构建步骤主要包括：

S1、网络初始化，确定储备池的层数K，K>1及初始化储备池的内部参数，内部参数包括储备池规模N，稀疏度α，谱半径SR、输入尺度IS以及遗忘率γ，根据内部参数生成投影矩阵和储备池内部递归矩阵，选取一种非监督的降维编码器并设置编码器的编码器维度；

(本实施例中参数为编码器维度)；

S2、信号输入，输入初始信号u，令Uⁱ＝u，其中，Uⁱ表示第i层储备池的输入信号，当i＝1时即为初始信号；

S3、状态更新，将Uⁱ作为输入信号输入到第i层储备池中，实现将Uⁱ投影到高维的回声状态空间中，得到输出信号在i层储备池中的所有时刻上的回声状态

S4、循环条件判断，如果i＜K，K为储备池的层数，进入步骤S5，否则，进入步骤S7；

S5、降维编码，将第i号储备池中的回声状态作为第i层编码器的输入信息，进行降维压缩，得到编码器的特征表示其中，表示紧随第i层储备池之后编码器的特征表示；

S6、循环操作，令作为下一个储备池的输入信息，即令第i层储备池的输入信号i＝i+1；返回步骤S2；

S7、模型求解，将直接连接信息u、编码器的特征表示及输出层的信息收集到矩阵M中，并通过线性回归技术学习相应的连接权值，将教师信号收集至矩阵T中，通过引入Tikhonov正则化项,构建岭回归问题实现对深度编码回声状态网络模型最优权重矩阵W^out的求解。

为了详细说明本实施例中基于多次编码重投影的深度回声状态网络的具体实施方式，以具有时间序列特性的数据集为例说明。该数据集包括Mackey-Glass System、Tenth-Order NARMA System、Monthly Sunspot Series Forecasting、Daily Minimum Temperatures Prediction四个部分，通过具体步骤如下:

S1、网络初始化，确定储备池的层数K(K>1)及初始化储备池的内部参数，包括储备池规模N，稀疏度α，谱半径SR、输入尺度IS以及遗忘率γ，根据这些参数生成投影矩阵和储备池内部递归矩阵，选取一种非监督的降维编码器并设置编码器的相关参数(本实施例中参数为编码器维度)；

选取主成分分析法为编码器，编码器维度大小设置为30，将层次化回声状态网络的层数设置为8，设置储备池内部参数：固定储备池规模大小N＝300，稀疏度α＝0.1，谱半径SR、输入尺度IS及遗忘率γ都控制在区间[0,1]，基于遗传算法优化选取每一层储备池所对应的SR、IS及γ，实验中遗传算法中的超参数设置：初始化种群大小为40，遗传代数为80.

S2、信号输入，输入初始信号u(t+1)；

S3、状态更新，将作为第t+1时刻输入信号输入到第i层储备池中，实现将投影到高维的回声状态空间中，得到第t+1时刻在i层储备池中的回声状态

即

其中，表示第i号储备池在第t+1时刻的输入，当i＝1时，f为激活函数，取为正切函数tan(·)，其中u(t+1)为步骤S2中输入的初始信号。

S4、循环条件判断，如果i＜K，K为储备池的层数，进入步骤S5，否则，进入步骤S7；

S5、降维编码，将第i层储备池中的回声状态作为第i层编码器在第t+1时刻的输入信息，进行降维压缩，得到编码器的特征表示

其中，表示紧随第i层储备池之后编码器在第t+1时刻的特征表示，fenc(·)是编码器的激活函数。

S6、循环操作，令作为下一个储备池的输入信息，即令第i层储备池的输入信号i＝i+1；返回步骤S2；

S7、模型求解，将直接连接信息u、编码器的特征表示及输出层的信息收集到矩阵M中，并通过线性回归技术学习相应的连接权值，将教师信号收集至矩阵T中，通过引入Tikhonov正则化项,构建岭回归问题实现对深度编码回声状态网络模型最优权重矩阵W^out的求解。

即令

输出第t+1时刻深度编码回声状态网络的预测值

y(t+1)＝f^out(W^outM(t+1)) (5)

即Y＝f^out(W^outM) (6)

根据整个系统的平方误差损失最小化，

采用Tikhonov正则化求解岭回归问题得

W^out＝TM^T(MM^T+βI)^-1 (8)

其中，正则化常数β设置为10^-5。

实验结果表明：基于编码重投影的层次化回声状态网络能够充分利用传统回声状态网络中时序核的特性去探索时间序列的多尺度动态结构，在混沌系统的时间序列预测中相比于其他层次化储备池计算模型表现出更优的性能，且其时间复杂度上保持了传统的回声状态网络的高效计算的特点。

上述实施例为本发明较佳的实施方式，但本发明的实施方式并不受上述实施例的限制，其他的任何未背离本发明的精神实质与原理下所作的改变、修饰、替代、组合、简化，均应为等效的置换方式，都包含在本发明的保护范围之内。