基于Elman神经网络的紧耦合无迹卡尔曼跟踪滤波算法的制作方法

本发明涉及目标跟踪技术，具体涉及一种基于elman神经网络的紧耦合无迹卡尔曼跟踪滤波算法。

背景技术：

机动目标跟踪系统中最基本的问题就是状态估计问题，也就是常见的滤波问题。随着机动目标跟踪技术的研究不断深入，涌现了很多实用的滤波算法，如卡尔曼滤波(kf)、扩展卡尔曼滤波(ekf)、无迹卡尔曼滤波(ukf)等等。这些基本的滤波算法结合时下较为成熟的机动目标运动模型即可很好地机动目标进行跟踪。但近年来，国内外科学技术日新月异，目标的机动性能不断提高，机动目标的跟踪环境也愈加复杂，一些传统的机动目标运动模型和滤波算法在跟踪这类强机动目标或高误差目标时，其性能往往都会显著下降。面对这样严峻的挑战，机动目标跟踪的研究工作不仅仅要从运动模型入手，来建模出能适应这种强机动目标的运动模型，还需要对滤波算法进行优化调整，使得滤波算法能够适应于不同的机动场景。

目前而言，常见的滤波优化方法可以分成以下三种类型：一是对于滤波算法中的某些参数进行自适应调整，即根据某种动态调整策略或者引入加权因子的方式对参数进行机动大小的自适应调整。如检测自适应滤波算法就是根据新息过程的变化，设计出机动检测准则，一旦检测到目标机动时，立刻进行噪声方差的调整。二是利用机器学习或者神经网络的方法对目标的状态估计进行预测，使用预测值来更新当前时刻的状态估计。如基于交互多模型的优化估计滤波算法就是通过神经网络训练出机动大小与最优估计的拟合函数，从而预测出当前时刻的状态估计值来更新目标的最优估计。三是结合以上两种方式既对滤波参数进行自适应调整，同时也对状态估计进行优化更新。但这三种类型的优化方法都是在单次滤波结束之后进行方差或者估计值的调整，其优化过程相对于滤波有一定的滞后，仍旧会有一定的滞后误差。

技术实现要素：

本发明的目的在于提供一种基于elman神经网络的紧耦合无迹卡尔曼跟踪滤波算法，降低了滞后优化修正所带来的滤波误差，提高了滤波精度。

实现本发明目的的技术解决方案为：基于elman神经网络的紧耦合无迹卡尔曼跟踪滤波算法，包括如下步骤：

步骤1、初始化滤波参数，包括初始状态估计、状态协方差矩阵、过程噪声协方差矩阵和观测噪声协方差矩阵；

步骤2、根据上一时刻的状态估计计算sigma点和对应权值，进行sigma点预测加权求和，获得当前时刻的初始状态预测值；

步骤3、获取当前时刻的目标观测值，与步骤2的初始状态预测值作差，获得待测数据；

步骤4、选取历史观测值、二次状态预测值、状态估计值、初始状态预测值和过程噪声协方差的尺度因子构建训练数据集，训练elman神经网络；

步骤5、利用训练的elman神经网络，初步预测待测数据的相对机动误差和过程噪声尺度因子；

步骤6、根据初步预测的相对机动误差和过程噪声尺度因子调整目标状态方程，并对步骤1的每个sigma点进行二次预测，获得二次状态预测值和协方差矩阵；

步骤7、根据二次状态预测值和协方差矩阵进行量测更新，获得当前时刻滤波的最优估计。

本发明与现有技术相比，其显著优点是：本发明在常规无迹卡尔曼滤波的基础上，引入紧耦合模型对目标状态的预测阶段进行优化估计与反馈修正，并使用elman神经网络算法，对量测与状态预测值之差进行在线学习，获得目标相对机动误差和过程噪声协方差矩阵的尺度因子，在滤波过程中实时优化修正状态方程，降低了滞后优化修正带来的滤波误差，提高了滤波精度，对机动目标具有更好的适应能力。

附图说明

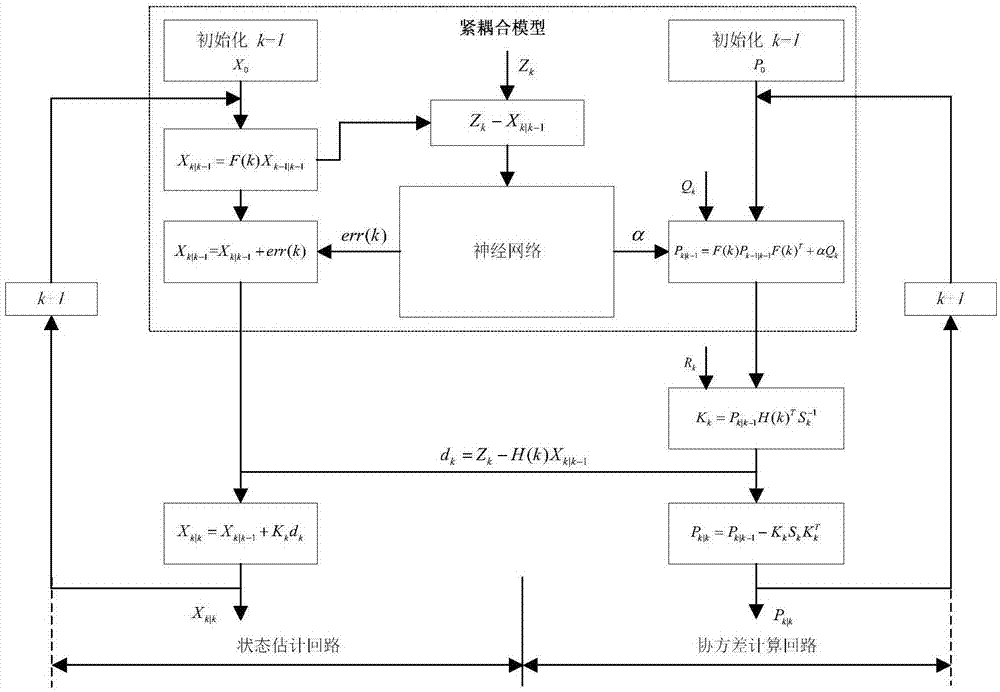
图1为紧耦合模型算法结构框图。

图2为本发明基于elman神经网络的紧耦合跟踪滤波方法的流程图。

图3为三种不同机动场景下的不同滤波算法的滤波轨迹图。

图4为三种机动情形下的1000次montecarlo仿真均值和均方根值分布图。

具体实施方式

下面结合附图和具体实施例对本发明方案作进一步的说明。

在目标跟踪系统中，常规的系统状态-空间方程定义如下：

其中，xk|k和zk分别表示状态向量与观测向量，f(k)与h(k)分别表示系统的状态转移矩阵与观测矩阵，ωk与vk分别代表过程噪声误差与量测噪声误差。

在机动目标存在不可忽略的机动误差，故可将状态-空间方程中的状态方程改写为：

xk|k＝f(k)xk-1|k-1+err(k)+αωk

其中，err(k)表示k时刻下系统所存在的相对机动误差，即k时刻下的目标状态方程描述与实际机动情形的相对误差，该误差是一个时变的量，但与目标的机动存在着一定的关联，故而可以通过一些方法估计出err(k)；α是描述过程噪声的尺度因子，用于调整目标状态方程，以便保证相对机动误差err(k)仅受每个时刻的机动影响，而不会掺杂过程状态误差信息。

在无迹卡尔曼滤波中，状态的一步预测变为：

xk|k-1＝f(k)xk-1|k-1+err(k)

而协方差矩阵的一步预测变为：

pk|k-1＝f(k)pk-1|k-1f(k)^t+αqk

只要相对机动误差err(k)与过程噪声尺度因子α足够精确，那么就能够使得状态预测值尽可能逼近目标实际位置，并及时调整状态方程描述。

因此，可定义如下计算方程：

[err(k),α]＝f(mk)

其中，mk表示k时刻的机动大小，f(·)表示mk与[err(k),α]之间的一种函数对应关系。

在状态方程的预测阶段，所能得到的有用信息只有目标的状态-空间方程和当前时刻的量测值。那么，当目标采样率足够小时，可以假设在状态的一步预测阶段，目标状态方程已调整至最优(即上一时刻的最优状态方程)，此时目标的状态预测值与量测值的差和当前时刻的机动也存在某种函数对应关系，即：

zk-xk|k-1＝g(mk)

而必定存在一个函数对应关系h(·)使得：

f(mk)＝h(g(mk))

那么，目标函数可转化成：

[err(k),α]＝h(zk-xk|k-1)

因此，本发明用神经网络对h(·)进行函数学习拟合，具体结构框图如图1所示。

此外，为了保证后续算法实验不会受到运动模型的影响，本发明运动模型采用ca模型，即：

观测函数为简单的以雷达坐标为原点的直角坐标系到极坐标系的空间坐标转换函数，具体的跟踪滤波方法流程如图2所示。

基于elman神经网络的紧耦合跟踪滤波方法，包括如下步骤：

步骤1、初始化滤波参数，包括初始时刻的目标量测初始化状态估计x0|0、状态协方差矩阵p0|0、过程噪声协方差矩阵q0和观测噪声协方差矩阵r0；

步骤2、根据上一时刻的状态估计计算sigma点和对应均值与方差加权值wi^(m)与wi^(c)，进行sigma点预测加权求和，获得当前时刻的初始状态预测值具体过程如下：

步骤2.1、根据上一时刻的状态估计xk-1|k-1，i＝1,…,2n，计算sigma点是无迹卡尔曼滤波的关键步骤，这些样本点可以准确获得高斯随机变量的均值和均方差，从而可以近似地表示状态变量的分布。sigma点χi和对应均值与方差加权值wi^(m)与wi^(c)的产生函数分别为：

其中，是(n+κ)·p(k-1|k-1)的均方根矩阵的第i行或列，p(k-1|k-1)表示上一时刻的协方差矩阵，n表示量测向量的维数，κ为满足n+κ≠0的任意值；

步骤2.2、基于ca模型，通过转移函数f(.)对sigma点进行状态转移变换，得到一组新的sigma点

步骤2.3、根据新sigma点和对应的均值加权值wi^(m)，计算初始状态预测值

步骤3、获取当前时刻的目标观测值zk，与步骤2的初始状态预测值作差，获得待测数据，

步骤4、选取固定时间段大小内的历史观测值z、二次状态预测值状态估计值x、初始状态预测值和过程噪声协方差的尺度因子α^*，构建训练数据集训练elman神经网络，具体过程如下：

步骤4.1、初始化神经网络参数，包括状态向量的维数m、量测向量的维数n、学习率l、承接层单元与隐藏层单元的连接权矩阵w¹，输入层单元与隐藏层单元的连接权矩阵w²，隐藏层单元与输出层单元的连接权矩阵w³为，创建一个含有m个输出层单元、2m个隐藏层单元和n个输出层单元的elman神经网络；

步骤4.2、对于每组训练数据循环执行以下步骤4.2.1～4.2.5进行训练，直至循环结束，其中z为历史观测值、为二次状态预测值、x为状态估计值、为初始状态预测值，α^*为过程噪声协方差的尺度因子；

步骤4.2.1、对于输入层数据u(k)和上一时刻的承接层数据xc(k-1)分别进行加权处理，并将所得结果进行叠加作为隐藏层的输入

步骤4.2.2、使用隐藏层的激活函数f(·)，即sigmoid函数，获得隐藏层的输出，该输出值既是输出层的输入数据x(k)，又是承接层用于下一时刻加权处理的输入数据xc(k)：

步骤4.2.3、输出层使用线性组合函数g(·)来对输入数据进行加权处理，获得最终输出结果y(k)：

y(k)＝g(w³x(k))

步骤4.2.4、使用误差函数e(k)来计算输出误差大小，若计算得到的误差小于预设的阈值则跳出循环并跳转至步骤4，否则，转至步骤3.2.5；

其中，表示理论输出结果；

步骤4.2.5、根据bp算法更新权值w¹,w²,w³，并继续循环训练测试数据：

步骤5、利用训练的elman神经网络h(·)，初步预测待测数据的相对机动误差和过程噪声尺度因子[err(k),α]；

步骤6、根据初步预测的相对机动误差和过程噪声尺度因子调整目标状态方程并对步骤1的每个sigma点进行二次预测，获得二次状态预测值和协方差矩阵pk|k-1，具体计算方法如下：

其中，qk表示当前时刻的过程噪声。

步骤7、根据二次状态预测值和协方差矩阵进行量测更新，获得当前时刻滤波的最优估计xk|k，具体过程如下：

步骤7.1、对二次状态预测值再次进行ut变换，获得新的sigma点集

步骤7.2、利用训练好的elman神经网络h(·)，对新的sigma点集进行观测预测，获得每个点的预测值

步骤7.3、对预测值进行加权，求观测预测值预测协方差矩阵pxz和新息协方差矩阵pzz：

其中，rk表示当前时刻的观测噪声协方差矩阵；

步骤7.4、计算滤波器的增益矩阵kk：

步骤7.5、计算当前时刻的滤波状态估计值xk|k，并更新状态协方差矩阵pk|k：

其中，zk|k表示当前时刻的目标观测值。

为了验证本发明方案的效果，进行如下机动形式的适应性实验。

场景一中目标以v＝200m/s的恒定速度在空中以设定好的双s形弯道飞行，期间目标最大的机动加速度为amax＝16m/s²，属于弱机动场景；场景二中目标以初速度v0＝200m/s，恒定加速度a＝2m/s²在设定好的单s形弯道飞行，期间目标最大机动加速度为amax＝64m/s²，属于较强机动场景；场景三中目标以初速度v0＝300m/s的恒定速度在空中以设定好的螺旋形弯道飞行，期间目标最大机动加速度为amax＝90m/s²，属于强机动场景。上述三种场景均模拟了δr＝300m,δa＝0.5°,δe＝0.5°大小的高斯白噪声。图3分别是三种机动情形下imm_elm模型、elm_ukf模型和紧耦合模型的滤波轨迹图；图4是三种机动情形1000次montecarlo仿真的位置误差均值和均方根值的分布图，统计计算结果如表1。

由图3可以定性分析得到，对于不同的机动形式与机动大小，imm_elm模型、elm_ukf模型以及紧耦合模型优化滤波算法都可以很好地进行机动目标跟踪，但很明显可以看出紧耦合模型的跟踪收敛效果要更好一些。由图4和表1可以定量分析得到，紧耦合模型与elm_ukf模型相比，在三种机动场景下，其滤波误差均值分别降低了23.14％、13.45％、18.68％，滤波误差均方根值分别降低了19.03％、6.54％、17.72％。可以看出，紧耦合模型在三种机动场景下均有着相对不错的跟踪性能。

表1三种机动情形下的1000次montecarlo仿真均值和均方根值统计表