卷积神经网络分数阶误差反向传播方法与流程

本发明属于人工智能算法领域，特别涉及了一种卷积神经网络分数阶误差反向传播方法。

背景技术

卷积神经网络是人工智能领域的算法，从自动驾驶的汽车到google的图像查找，都可以运用卷积神经网络实现。卷积神经网络中训练过程是一个非常重要的部分，在该过程中一般通过反向传播方法使网络权值(滤波器)不断更新调整，直至网络的输出与目标趋于一致。反向传播方法的过程共分为4个基本步骤：前向传播、损失计算、反向传播、权值更新。然而，在“反向传播”步骤中，常常会出现因“梯度消失”现象导致网络难以训练的问题。因此，有效改善“梯度消失”是卷积神经网络得以正常训练，从而获得精确网络参数的重要保证。

目前，分数阶微积分与神经网络的结合已成为人工智能领域的研究热点，分数阶神经网络的应用表明比传统神经网络具有更大的优势。《基于分数阶卷积神经网络的语音识别算法研究》(张磊.哈尔滨理工大学,2016.)直接使用分数阶方法对激活函数进行处理，采用分数阶激活函数参与网络训练，提高了卷积神经网络的训练速度。《分数阶理论在bp神经网络中的应用》(陈小磊.南京林业大学,2013.)在卷积神经网络训练反向传播过程中，直接对误差求分数阶偏导数，并进行变阶次的迭代学习，实现了分数阶次与整数阶次的切换和分数阶次的自适应调整，使得网络训练既具有收敛速度又有好的收精度。专利申请《一种改进卷积神经网络结构的方法》(公开号：cn106960243a)利用分数阶最大值池化原理，将传统卷积神经网络结构中的最大值池化层全部更改为分数阶，达到图像任意维度的下采样降维，提高了网络训练效率。上述算法虽然与传统算法相比有一定优势，但“松散”的结合方式并没有探究分数阶理论与卷积神经网络理论结合问题的实质。有针对性的改进卷积神经网络的训练过程，才能进一步提高网络参数精度，提高网络性能。

技术实现要素：

本发明的目的是克服上述背景技术的不足，实现了分数阶与卷积神经网络理论的“紧密”结合，提供了一种卷积神经网络分数阶误差反向传播方法，具体由以下方案实现：

所述卷积神经网络分数阶误差反向传播方法,包括如下步骤：

步骤1)选择卷积神经网络模型；

步骤2)利用分数阶误差反向传播方法更新网络权值；

步骤3)根据所述的网络权值，获取卷积神经网络参数。

所述卷积神经网络分数阶误差反向传播方法的进一步设计在于，所述步骤1)具体包括：

步骤1-1)设定神经网络模型，所述神经网络模型包括一层输入层、n层隐藏层以及一层输出层，所述输入层、隐藏层、输出层的节点个数分别对应为n1，n2，1个；

步骤1-2)设定大量高分辨率图像{xi}和其对应的低分辨率图像{yi}组成的训练集，其中：x表示高分辨率图像，y表示低分辨率图像，i表示图像索引；步骤1-3)设定卷积神经网络的权值和偏置为θ＝{w,b}，设定误差函数和激活函数分别为l和σ，其中w表示权值，b为偏置。

所述卷积神经网络分数阶误差反向传播方法的进一步设计在于，所述步骤2包括以下子步骤：

步骤2-1)网络初始化：初始化网络权值和偏置θ＝{w1,b1}，设置最大迭代次数；

步骤2-2)输入训练数据{xi,yi}；

步骤2-3)设置初始迭代次数k＝1；

步骤2-4)对网络权值进行优化；

步骤2-5)根据k＝k+1更新迭代次数，并跳转到步骤2-4)。

所述卷积神经网络分数阶误差反向传播方法的进一步设计在于，步骤2-4)对网络权值进行优化具体包括以下步骤：

步骤2-4-1)计算网络输出值；

步骤2-4-2)计算误差：采用所述误差函数，计算网络输出值和真实值之间的误差，判断误差是否满足要求，如果满足要求，则网络训练结束转入步骤3)；如果不满足要求，则进行权值修正，进入步骤2-4-3)；

步骤2-4-3)计算误差反向传播梯度中激活函数的分数阶导数，并计算每个神经元节点的分数阶导数；

步骤2-4-4)计算误差梯度；

步骤2-4-5)修正权值：根据误差关于权重的梯度，修正网络权值。

所述卷积神经网络分数阶误差反向传播方法的进一步设计在于，所述步骤2-4-3)中根据式(1)计算误差反向传播梯度中激活函数的分数阶导数：

其中，grad^l表示第l层的误差反向传播梯度，为激活函数的输入，即网络节点的输出，表示第(l-1)层的第个神经元连接到第层的第j个神经元的权重，表示第l层的第j个神经元的偏置，μ表示分数阶导数的阶次，⊙为矩阵对应位置乘积，表示矩阵或向量之间点对点的乘法运算；

根据式(2)计算每个神经元节点的分数阶导数：

其中，为分数阶微分算子，d为1阶微分算子，x表示神经网络节点的输出值，σ(x)表示激活函数，σ′(x)表示激活函数的1阶导数，μ表示分数阶微分的阶次，γ(x)为gamma函数，定义为且re(x)＞0。

所述卷积神经网络分数阶误差反向传播方法的进一步设计在于，步骤2-4-5)采用经典随机梯度下降法根据式(3)修正权值,

其中，i表示网络层数，η表示学习率，通过线搜索的方式获得，表示激活函数的分数阶导数。

所述卷积神经网络分数阶误差反向传播方法的进一步设计在于，步骤1-3)中的激活函数σ表达式如式(4)：

其中，x为网络节点输出值。

本发明的有益效果为：

本发明的卷积神经网络分数阶误差反向传播方法将误差反向传播过程中激活函数的整数阶导数变为分数阶导数，发挥了分数阶求导模型比整数阶求导模型更加准确的优势，有效缓解了误差反向传播过程中的“梯度消失”问题，提高了卷积神经网络的训练效率，使卷积神经网络对于训练数据实现更好的拟合，提高了网络的泛化能力。

附图说明

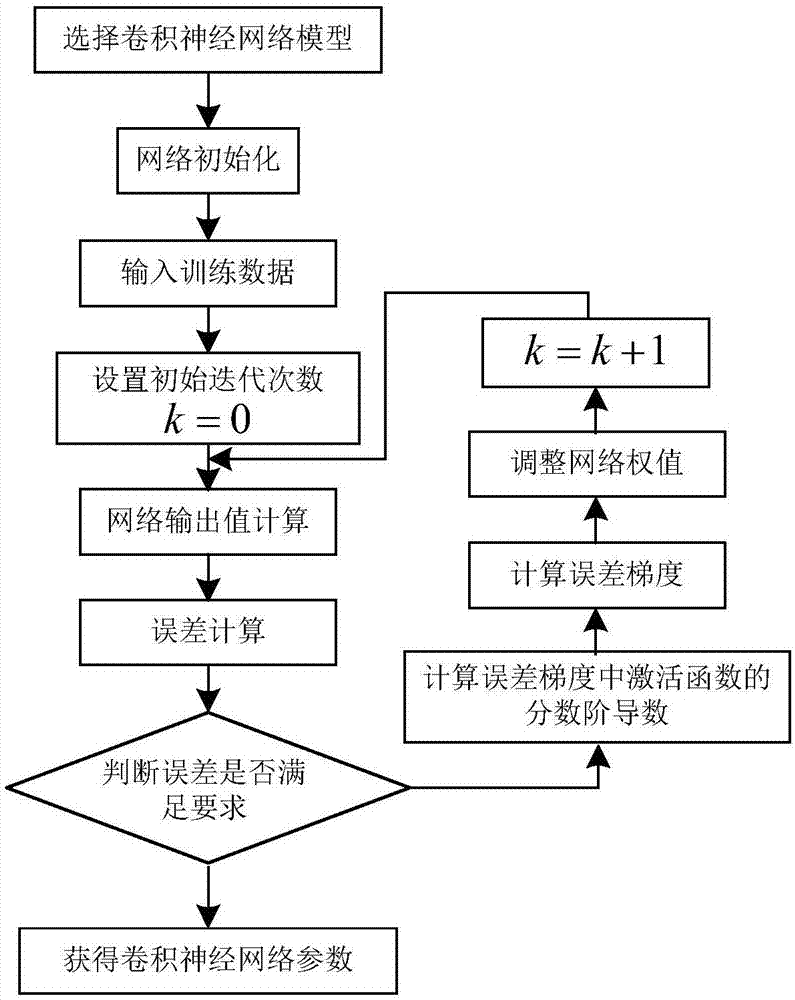
图1是本发明提供的卷积神经网络分数阶误差反向传播方法流程图。

图2是本发明提供的分数阶误差反向传播神经网络模型(每层只有一个神经元)示意图。

具体实施方式

以下将结合附图，对本发明的技术方案进行详细说明。

如图1所示，卷积神经网络分数阶误差反向传播方法的基本步骤如下：

步骤1)选择卷积神经网络模型。

步骤2)利用分数阶误差反向传播方法更新网络权值。

步骤3)根据所述的网络权值，获取卷积神经网络参数。

优选的，本实施例的步骤1)卷积神经网络模型如下：

步骤1-1)选择四层神经网络模型，包括1层输入层，n层隐藏层，1层输出层，所述输入层、隐藏层、输出层节点个数分别为n1，n2，1个。

步骤1-2)选择大量高分辨率图像{xi}和其对应的低分辨率图像{yi}组成的训练集。

步骤1-3)卷积神经网络的权值和偏置记为θ＝{w1,w2,...,wn+1,b1,b2,...,bn+1}，误差失函数和激活函数分别记为l和σ。

进一步优选的，本实施例的步骤1)中误差函数l表达式如式(1)：

式中n是训练样本的数量，f是高低分辨率图像端到端的映射函数，

f(yi,θ)表示网络预测值，x表示目标值。

进一步优选的，本实施例的步骤1)中的激活函数σ表达式为：

其中，x为网络节点输出值。

优选的，本实施例的步骤2)包括如下子步骤：

步骤2-1)网络初始化。初始化网络权值和偏置，其中权值初始化为均值为0，标准差为0.001的高斯分布，偏置初始化为0；设置最大迭代次数k；

步骤2-2)输入训练数据{xi,yi}；

步骤2-3)设置初始迭代次数k＝1；

步骤2-4)对网络权值进行优化；

优选的，步骤2-4)对网络权值进行优化包括以下步骤：

步骤2-4-1)计算网络输出值；

步骤2-4-2)计算误差。采用所述误差函数，计算网络输出值和真实值之间的误差，判断误差是否满足要求。如果满足要求，则网络训练结束转入步骤3；如果不满足要求，且迭代次数未达到设定最大次数k，则进行权值修正，进入步骤2-4-3；

步骤2-4-3)计算误差反向传播梯度中激活函数的分数阶导数。对每个神经元节点采用相同阶次的分数阶导数；

误差反向传播梯度计算表达式为：

其中，grad^l表示第l层的误差反向传播梯度，为激活函数的输入，即网络节点的输出，表示第(l-1)层的第个神经元连接到第层的第j个神经元的权重，表示第l层的第j个神经元的偏置，μ表示分数阶导数的阶次，⊙为hadamard乘积(矩阵对应位置乘积)，表示矩阵或向量之间点对点的乘法运算；

分数阶导数计算公式为：

其中，为分数阶微分算子，d为1阶微分算子，x表示神经网络节点的输出值，σ(x)表示激活函数，σ′(x)表示激活函数的1阶导数，μ表示分数阶微分的阶次，γ(x)为gamma函数，定义为且re(x)＞0。

步骤2-4-4)计算误差梯度。

步骤2-4-5)修正权值。根据误差关于权重的梯度，采用经典随机梯度下降法修正网络权值。权值更新方式为：

其中，i表示网络层数，η表示学习率，通过线搜索的方式获得。

步骤2-5)k＝k+1，转到步骤2-4)。

以上所述，仅为本发明较佳的具体实施方式，但本发明的保护范围并不局限于此，任何熟悉本技术领域的技术人员在本发明揭露的技术范围内，可轻易想到的变化或替换，都应涵盖在本发明的保护范围之内。因此，本发明的保护范围应该以权利要求的保护范围为准。