基于节气特征的土遗址温度预测方法与流程

本发明属于信号与信息处理技术领域，进一步涉及温度预测，具体为一种基于节气特征的土遗址温度预测方法，可用于预测土遗址所在环境的温度。

背景技术

土遗址是以土为主要建筑材料的具有历史、文化、和科学价值的古遗址，其不只是几千年来人类活动的痕迹，更是历史信息的重要载体，具有极高的研究价值。作为四大文明古国中唯一将文明绵延、不断传承至今的国家，中国土遗址的研究与保护问题更应被重视。土遗址的研究在国外开始较早，然而大部分都是针对露天环境所进行的。在20世纪80年代，我国开始进行土遗址的研究与保护工作，但专门针对室内封闭环境中土遗址问题的研究依然较少。位于陕西咸阳的汉阳陵外葬坑遗址是我国第一座全封闭式土遗址博物馆，该馆通过全封闭的展品成列模式将遗址保护区与游客参观区隔离开，有效避免了游客与遗址直接接触所造成的遗址破坏，然而温度、湿度等因素仍会对土遗址产生潜移默化的影响。

二十四节气是中国农历中表示季节变迁的24个节令，细致的反应了我国四季交替的气候特点，在时令、气候、物候、农作物生长等方面具有标志性意义。二十四节气起源于古代黄河流域。公元前104年，由邓平等人制订的我国第一部有完整文字记载的历法——《太阳历》，将二十四节气订于历法，明确了其天文位置。根据地球在黄道(即地球公转轨道)上的位置变化，从黄经零度起，地球每运行15度便将该日期命名为一个节气；地球一年共运行360度，即一年共有24个节气。反映四季变化的节气有：立春、春分、立夏、夏至、立秋、秋分、立冬、冬至8个节气；反映温度变化的有：小暑、大暑、处暑、小寒、大寒5个节气；反映天气现象的有：雨水、谷雨、白露、寒露、霜降、小雪、大雪7个节气；反映物候现象的有惊蛰、清明、小满、芒种四个节气。温度、湿度等会对土遗址产生影响的这类因素均可通过节气反映出来。

许多针对不同应用的温度预测方法在文献中已被提出，例如：利用回归拟合的方法建立夯土建筑遗址表面温度预报模型、利用线性拟合的方法建立某些环境下的温度预测模型、利用支持向量机建立农业大棚温室的温度预测模型，以及基于统计理论的温度预测方法等。另外，基于神经网络的温度预测方法也被提出，例如：基于bp神经网络、rbf神经网络的温度预测方法等。然而，这些预测温度的方法，在对土遗址的研究与保护方面应用较少，并且存在较大误差。

技术实现要素：

本发明的目的在于克服上述现有技术存在的缺陷，提出了一种基于节气特征的土遗址温度预测方法。该方法引入神经网络，在年、日、时分秒特征的基础上，利用隶属度函数再加入节气特征来进行温度预测，从而降低了预测时产生的相对误差，提高了温度预测的精确度。

为实现上述目的，本发明采用的技术方案包括如下步骤：

(1)提取时间特征：

(1.1)从历年实测的土遗址温度数据中选取n个数据作为数据样本，其中n为大于等于1的整数；

(1.2)输入数据样本所对应的时间矩阵t：

t＝[t1,t2,…,tj,…,tn]^t，

其中，tj表示第j个土遗址温度数据所对应的时间，其单位为：天，1≤j≤n且j为整数；[·]^t表示矩阵的转置操作；

设矩阵t中所有元素的最小值为tmin、最大值为tmax；

(1.3)计算数据样本中第j个土遗址温度数据的时间特征，包括时分秒特征α1j、日特征α2j及年特征α3j：

α1j＝tjmod1，

其中，mod表示求余运算符，表示向下取整操作；

(2)提取节气特征：

(2.1)选取m个连续的节气点，输入其所对应的时间矩阵z：

z＝[z1,z2,…,zi,…,zm]^t，

其中，m为大于等于1的整数；zi表示第i个节气点所对应的时间，其单位为：天，1≤i≤m且i为整数；[·]^t表示矩阵的转置操作；

设矩阵z中所有元素的最小值为zmin、最大值为zmax，且zmin≤tmin、zmax≥tmax；

(2.2)通过隶属度函数计算第j个土遗址温度数据的节气特征α4j：

其中，为时间tj之前距离其最近的节气点所对应的时间，为时间tj之后距离其最近的节气点所对应的时间；为tj对的隶属度函数，为tj对的隶属度函数；

(3)获取数据样本的总特征：

计算第j个土遗址温度数据的总特征xj：

xj＝ω1α1j+ω2α2j+ω3α3j+ω4α4j<1>

其中，ω1、ω2、ω3和ω4依次为土遗址温度数据的时分秒特征、日特征、年特征和节气特征的权值；

取j为1到n，通过公式<1>计算得到数据样本的总特征矩阵x：

x＝[x1,x2,…,xj,…,xn]^t；

(4)使用神经网络预测土遗址温度：

(4.1)由数据样本确定用于训练的土遗址温度数据矩阵γ：

γ＝[τ1,τ2,…,τj,…,τn]^t，

其中，τj为数据样本中的第j个土遗址温度数据；

(4.2)将数据样本的总特征矩阵x作为神经网络的输入层输入矩阵，将土遗址温度数据矩阵γ作为神经网络的输出层期望输出矩阵，利用神经网络进行学习训练，得到土遗址温度预测的神经网络模型；

(4.3)设待预测土遗址温度数据的总特征矩阵为xc，将其作为输入层输入矩阵代入到该土遗址温度预测的神经网络模型中，得到输出层输出矩阵，即为土遗址温度预测结果矩阵。

本发明与现有技术相比，具有如下优点：

第一：由于本发明利用隶属度函数建立了节气点与各温度数据所对应的时间之间的联系，有效解决了节气点分散且所对应的时间无法与各温度数据所对应的时间一一对应的问题，使得节气特征的提取更加准确；

第二：由于本发明在进行温度预测的过程中，不仅仅使用了年、日、时分秒特征，还综合考虑到节气特征，从而有效提高了温度预测的精度，降低了预测温度时产生的相对误差。

附图说明

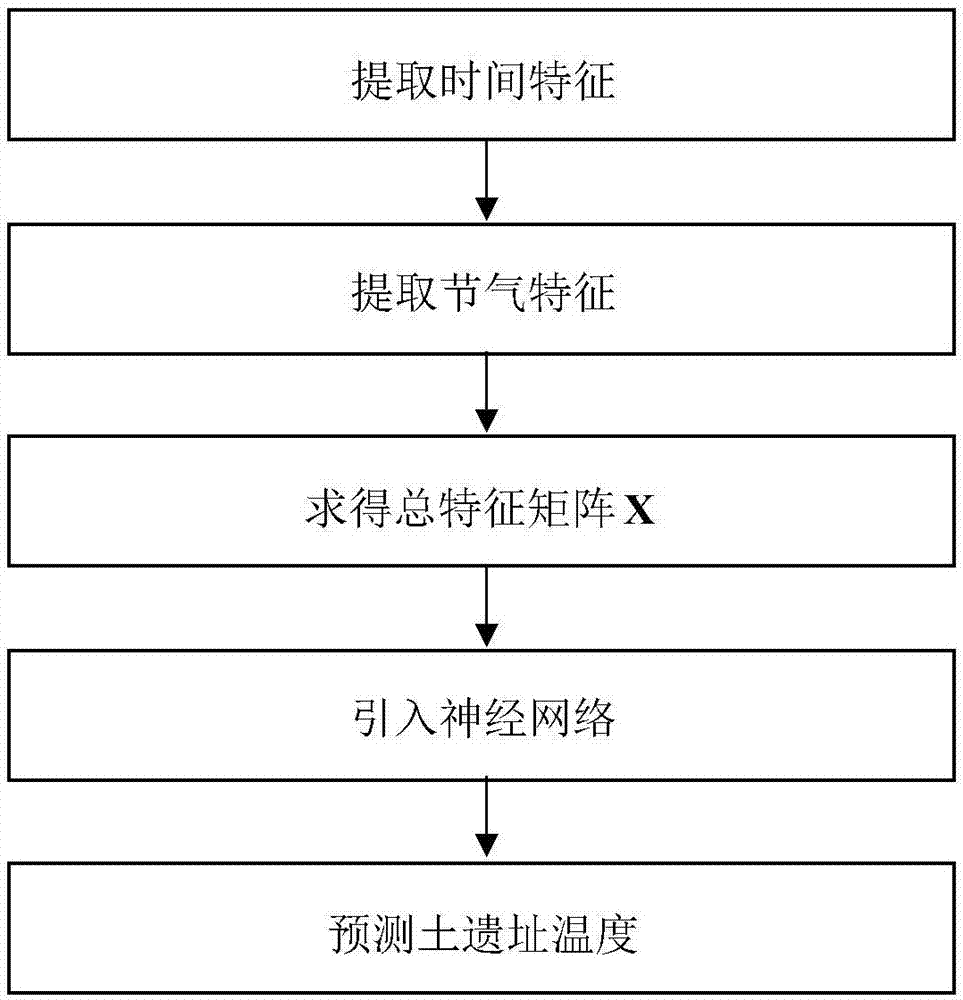
图1为本发明的实现流程图；

图2为相邻两节气的高斯隶属度函数图；

图3为2011年110116号站点温度随天数变化的数据图；

图4为2011年110116号站点温度随节气变化的数据图；

图5为2011年110116号站点第110天至117天加入节气特征后随机抽点的预测结果图；

图6为2011年110116号站点第110天至117天加入节气特征与不加入节气特征的相对误差对比图；

图7为2011年110116号站点第110天至140天加入节气特征后随机抽点的预测结果图；

图8为2011年110116号站点第110天至140天加入节气特征与不加入节气特征的相对误差对比图；

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，下面结合附图及具体实施例对本发明做进一步描述。

参照图1，本发明的具体实现步骤如下：

步骤1，提取时间特征：

(1.1)从历年实测记录的土遗址温度数据中选取n个数据作为数据样本，其中n为大于等于1的整数；

(1.2)输入数据样本所对应的时间矩阵t：

t＝[t1,t2,…,tj,…,tn]^t，

其中，tj表示第j个土遗址温度数据所对应的时间，以公元0年为正负分界，其单位为：天，1≤j≤n且j为整数；[·]^t表示矩阵的转置操作；

设矩阵t中所有元素的最小值为tmin、最大值为tmax；

(1.3)时分秒特征、日特征、年特征统称为时间特征，计算数据样本中第j个土遗址温度数据的时间特征，包括时分秒特征α1j、日特征α2j及年特征α3j：

α1j＝tjmod1，

其中，mod表示求余运算符，表示向下取整操作；

步骤2，提取节气特征：

(2.1)选取m个连续的节气点，其中m为大于等于1的整数，输入其所对应的时间矩阵z：

z＝[z1,z2,…,zi,…,zm]^t，

其中，zi表示第i个节气点所对应的时间，其单位为：天，1≤i≤m且i为整数；[·]^t表示矩阵的转置操作；

设矩阵z中所有元素的最小值为zmin、最大值为zmax，且zmin≤tmin、zmax≥tmax；

(2.2)引入隶属度函数，计算第j个土遗址温度数据的节气特征α4j：

其中，为时间tj之前距离其最近的节气点所对应的时间，为时间tj之后距离其最近的节气点所对应的时间；为tj对的隶属度函数，为tj对的隶属度函数；

将第j个土遗址温度数据所对应的时间tj与矩阵z中所有元素逐一进行大小比较并计算差值，选取所有差值中最小的两个，则这两个最小值所对应的矩阵z中元素即为和

常用的隶属度函数有高斯隶属度函数、sigmoid隶属度函数、钟型隶属度函数、抛物型隶属度函数以及自定义的隶属度函数等，这里本实施例取高斯隶属度函数，图像如图2所示，具体通过下式计算和

其中，均值μ＝0，标准差σ＝3.7；

步骤3，获取数据样本的总特征：

计算第j个土遗址温度数据的总特征xj：

xj＝ω1α1j+ω2α2j+ω3α3j+ω4α4j<1>

其中，ω1、ω2、ω3和ω4依次为土遗址温度数据的时分秒特征、日特征、年特征和节气特征的权值，这里的权值均为经验所得，且为常数，但针对不同数据可能会产生不同的取值。这里本实施例取时间特征权值当加入节气特征时，取节气特征权值否则ω4＝0。

取j为1到n，通过公式<1>计算得到数据样本的总特征矩阵x：

x＝[x1,x2,…,xj,…,xn]^t；

步骤4，使用神经网络预测土遗址温度：

这一步所使用的神经网络可以是单隐层前馈神经网络、反向传播神经网络、卷积神经网络等多种神经网络中的任意一种，本实施例以单隐层前馈神经网络为例，具体预测步骤如下：

(4.1)由数据样本确定用于训练的土遗址温度数据矩阵γ：

γ＝[τ1,τ2,…,τj,…,τn]^t，

其中，τj为数据样本中的第j个土遗址温度数据；

(4.2)求土遗址温度预测的神经网络模型：

(4.2.1)将数据样本的总特征矩阵x作为神经网络的输入层输入矩阵，得到关于总特征矩阵x的隐含层输出矩阵η(x)：

其中，l为隐含层神经元个数，且为大于等于1的整数；ak为输入层与隐含层第k个神经元之间的连接权值，bk为隐含层第k个神经元的阈值，1≤k≤l且k为整数，ak与bk通过计算机随机生成；g(·)为激励函数，常用的激励函数有sin函数、sigmoid函数、hardlim函数等。这里本实施例设置激励函数形式为g(a,b,x)＝g(ax+b)，取sin函数作为激励函数，即g(a,b,x)＝sin(ax+b)。

(4.2.2)将土遗址的温度数据矩阵γ作为单隐层前馈神经网络的输出层期望输出矩阵；

(4.2.3)设隐含层与输出层之间的连接权值矩阵为β，且为一个l×1的矩阵，则：

η(x)β＝γ<2>

对式<2>进行变换得到：

其中，是η(x)的moore-penrose广义逆矩阵，可表示为·^t表示矩阵的转置操作，[·]^-1表示矩阵的逆。

通过式<3>计算得到出隐含层与输出层之间的连接权值矩阵β。

(4.3)进行土遗址温度预测：

(4.3.1)设待预测土遗址温度数据的总特征矩阵为xc，则隐含层输出矩阵为η(xc)；

(4.3.2)由下式计算得到土遗址温度预测结果矩阵y：

y＝η(xc)β。

本发明的效果可以通过以下仿真结果进一步说明：

1、仿真条件

下述仿真实验选取2011年110116号站点的部分温度数据及其所对应的时间数据作为输入，2011年110116号站点全年数据如图3和图4所示。时间特征权值设置为实验次数设置为100次，每次随机取出99％的温度数据及其所对应的时间数据用于训练，剩下的数据用于预测。

2、仿真内容

仿真1，输入2011年110116号站点第110天至117天(共7天)的温度数据及其所对应的时间数据。不引入节气特征，即ω4＝0，得到预测值与真实值的相对误差均值1.5×10^-3；引入节气特征，即得到预测值与真实值的相对误差均值3.3473×10^-4，其随机抽点的预测结果如图5所示。加入节气与不加入节气的相对误差对比如图6所示。

仿真2，输入2011年110116号站点第110天至140天(共30天)的温度数据及其所对应的时间数据。不引入节气特征，即ω4＝0，得到预测值与真实值的相对误差均值1.5×10^-3；引入节气特征，即得到预测值与真实值的相对误差均值5.9418×10^-4，其随机抽点的预测结果如图7所示。加入节气与不加入节气的相对误差对比如图8所示。

图5-图8表明，无论对与短时间的数据或是长时间的数据，加入节气特征都可以有效的提高温度预测精度、降低相对误差。

本发明未详细说明部分属于本领域技术人员公知常识。

以上描述仅是本发明的一个具体实例，并未构成对本发明的任何限制。显然对于本领域的专业人员来说，在了解了本发明内容和原理后，都可能在不背离本发明原理、结构的情况下，进行形式和细节上的各种修正和改变，但是这些基于本发明思想的修正和改变仍在本发明的权利要求保护范围之内。