DSA通孔层三重模式分解的离散松弛法的制作方法

本发明涉及一种dsa通孔层三重模式分解的离散松弛法，通过构造一个加权冲突分组图，引入负权重的边，然后提出了一个基于掩模板设计的离散松弛问题；用整数线性规划(ilp)公式来求解离散松弛问题，求得该问题最优值的下界；为了改善下界，引入一些有效的不等式来修正一些不好的松弛问题的解；最后，通过求解布局图上的模板设计问题，将得到的离散松弛解转化为原问题的合法解，从而为原问题的最优值提供了一个上界。

背景技术

随着间距尺寸的减小和节点数量的增加，集成电路(ic)布局的制造越来越困难。这促使一系列制造技术，如193纳米浸没光学光刻和相关的多重光刻技术，电子束光刻技术，嵌段共聚物的定向自组装和极紫外光刻技术。集成电路布局由模式线条和孔组成。这些线定义了有源器件区域，栅电极以及器件之间的布线。这些孔定义了导线和晶体管之间的电气通孔。上述一些制造技术普遍用于线条特征的布局，但dsa技术适用于密集通孔的模式。特别是在7nm节点上，接触/通孔层上的特征分布密集且对齐，因此dsa技术是必要的。

技术实现要素：

本发明的目的在于提供一种dsa通孔层三重模式分解的离散松弛法，通过构造一个加权冲突分组图，引入负权重的边，然后提出了一个基于掩模板设计的离散松弛问题；用整数线性规划(ilp)公式来求解离散松弛问题，求得该问题最优值的下界；为了改善下界，引入一些有效的不等式来修正一些不好的松弛问题的解；最后，通过求解布局图上的模板设计问题，将得到的离散松弛解转化为原问题的合法解，从而为原问题的最优值提供了一个上界。

为实现上述目的，本发明的技术方案是：一种dsa通孔层三重模式分解的离散松弛法，包括如下步骤：

步骤s1、构造一个加权冲突分组图，其中引入负权重的边，然后提出一个基于掩模板分配的离散松弛问题；

步骤s2、用整数线性规划ilp公式来求解离散松弛问题，求得该离散松弛问题最优值的下界；

步骤s3、为了改善下界，引入有效的不等式来修正离散松弛解；

步骤s4、通过求解布局图上的模板分配问题，将得到的离散松弛解转化为dsa的三重模式的掩模板和模板设计问题合法解，从而为dsa的三重模式的掩模板和模板设计问题的最优值提供了一个上界。

在本发明一实施例中，在冲突分组图cgg中，由冲突边连接的两个通孔应分配给不同的掩模板，或者由mtadt的模板分组；为了减少使用掩模板的冲突和总成本，需确定通孔、冲突边是否应分组，此处通过加权来区分冲突边，然后构造加权冲突分组图wcgg；为处理分组，引入一个负权重的边，具体定义如下：

令通孔i和j之间的边eij∈e的加权规则设置为

其中，e表示加权冲突分组图wcgg中的所有边的集合；ec表示加权冲突分组图wcgg中的冲突边的集合；eg表示加权冲突分组图wcgg中的分组边的集合；en表示加权冲突分组图wcgg中的负边的集合；

根据上面的加权规则，可知：

1)如果通孔i1，i2被设计到相同的掩模板，并且则通孔之间存在冲突，并且边成本为1.0；

2)如果通孔i1，i2被设计到相同的掩模板，并且那么边成本是0.03；

3)如果将通孔i1，i2,i3设计给相同的掩模板，并且则边成本为0.05；

4)如果将通孔i1，i2，...，ik，k＝3,4设计给相同的掩模板，并且i1，i2，...，ik满足有k个洞的模板tk的条件；可以推断出k-1条分组边和k-2条负边，并且边的成本是0.03(k-1)-0.01(k-2)＝0.01(2k-1)。

在本发明一实施例中，为了解决离散松弛问题p1，将离散松弛问题p1转换为整数线性规划ilp问题p2等价于如下：

在上述公式中，xim是一个二元变量，表示为通孔i设计的掩模板；如果xim＝1，那么i被设计给掩模板m；cij是一个二元变量，用于表示通孔i和j之间是否产生冲突；

在整数线性规划ilp问题p2中，约束公式(2a)被用来决定在通孔i和j之间是否有冲突cij；即对于eij∈e，如果通孔i和j在同一个掩模板中，则cij＝1；约束公式(2b)用于为通孔i选择掩模板；

求解整数线性规划ilp问题p2可获得dsa的三重模式的掩模板和模板设计问题p0的一个下界。

在本发明一实施例中，为了避免cis中的通孔点被设计到相同的掩模板中，通过添加三角形边将加权冲突分组图wcgg修改为新的加权冲突分组图wcgg，并且将每个三角边的权重设计为w＝λ；然后，给整数线性规划ilp问题p2增加四种新的约束，并将新的问题称为

对于“l”形结构，如果将三个通孔i，j和k设计给相同的掩模板，则由于角不兼容而至少存在一个冲突；为了获得更好的解，为“l”形结构的通孔i，j和k添加有效不等式，以避免将三个通孔i，j和k设计给相同的掩模板；有效不等式为：

xim+xkm+xjm≤2+cij，m＝1，2，3(3a)

而通孔k是一个角落通孔；约束公式(3a)用于限制，如果通孔i，j和k被设计到相同的掩模板，则三角形边的冲突变量eij∈et，具有cij＝1，其中et表示加权冲突分组图wcgg中的三角边的集合；

对于“t”形结构，如果四个通孔i，j，l和k被设计到相同的掩模板，则由于角不兼容而至少存在一个冲突；同样，为“t”形结构的四个通孔添加有效不等式：

xim+xkm+xjm≤2+cij+cjl，m＝1，2，3；(4a)

xjm+xkm+xlm≤2+cij+cjl，m＝1，2，3；(4b)

通孔k是一个角落通孔；如果三个通孔i，j和k或j，l和k或四个通孔被分配给相同的掩模板，则使用约束公式4(a)-4(b)来限制：至少一个三角形边eij和ejl的冲突变量等于1；

对于“z”形结构，如果将四个通孔i，j，l和k设计给相同的掩模板，则由于角不兼容而至少存在一个冲突；类似地，为“z”形状结构的四个通孔添加有效不等式：

xim+xkm+xjm≤2+cij+ckl，m＝1，2，3；(5a)

xjm+xkm+xlm≤2+cij+ckl，m＝1，2，3；(5b)

通孔k和j是角通孔；如果将三个通孔i，j和k或j，l和k或四个通孔设计给相同的掩模板，则使用约束公式5(a)-5(b)来限制：至少三角边eij和ekl的一个冲突变量等于1；

对于“+”形状结构，如果五个通孔i，j，l，h和k被设计到相同的掩模板，则由于角不兼容性而至少存在两个冲突；类似地，为“+”形状结构的五个通孔添加有效不等式：

xim+xkm+xjm≤2+cij+cjl，m＝1，2，3；(6a)

xjm+xkm+xlm≤2+cjl+clh，m＝1，2，3；(6b)

xlm+xkm+xhm≤2+clh+chi，m＝1，2，3；(6c)

xhm+xkm+xim≤2+chi+cij，m＝1，2，3；(6d)

通孔k是一个角通孔；如果将“l”形cis中的三个通孔或“t”形cis中的四个通孔设计给相同的掩模板，则使用约束公式6(a)-6(d)来限制，则至少三角边的一个冲突变量等于1；如果将“+”形cis中的五个通孔设计给相同的掩模板，则三角形边eij，ejl，elh和ehi中的两个冲突变量等于1。

在本发明一实施例中，所述步骤s4的实现方法为：假设sl是“l”形cis，i，j和k是sl的三个通孔点，k是角通孔，teij是三角边；令xl＝{xi1，xi2，xi3，xj1，xj2，xj3，xk1，xk2，xk3}；显然，xl是x的一部分；如果i，j是设计给不同的掩模板，为了最小化目标，那么三角边teij的冲突变量cij＝0；如果通孔k的掩模板与i和j的掩模板不同，则该等式表示问题在xl的值等于问题p0在处的值且等于0；如果k的掩模板与i和j的掩模板相同，比如说i，那么对于如果分组边geki由多孔模板指导，则否则在k和i之间会产生冲突，有无论如何，它保持

如果sl的所有通孔点i，j和k被设计到相同的掩模板，则约束公式(3a)将强制cij为1；一方面，另一方面，由于sl是“l”形cis，(1)如果在中，sl需要一个冲突和包含sl中的一条分组边的多孔模板，则sl的分解成本为(2)如果在中，sl需要两个冲突，则因此有

对于sl，有对于“t”形，“z”形和“+”形的cis，可以类似地证明，结论仍然成立；

因此，对于问题p0的最优解x⁰，以及从x⁰中通过省略模板设计而得到的x，保持因此问题仍然是问题p0的离散松弛问题；通过在软件包cplex中使用分支定界法来解决问题由于问题在大规模情况下难以解决，故而引入图剪枝技术来减小问题的规模。

在本发明一实施例中，所述图剪枝技术包括：连通分支的计算，度数小于3的点的删除和2边连通分支的计算；度数小于3的点的删除技术将删除部分通孔；此外，对于2边连通分支的计算，如果顶点i和j通过桥连接并在掩模板设计阶段被设计到相同的掩模板中，然后在i和j之间产生一个冲突；可通过旋转2边连通分支的其中一个的颜色来消除冲突，使得i和j处于不同的掩模板；而且，无需考虑i和j的模板设计。

相较于现有技术，本发明具有以下有益效果：本发明方法首先构造一个加权冲突分组图，其中引入了负权重的边，然后提出了一个基于掩模板分配的离散松弛问题；用整数线性规划(ilp)公式来求解离散松弛问题，求得该问题最优值的下界；为了改善下界，引入一些有效的不等式来修正一些不好的松弛问题的解；最后，通过求解布局图上的模板分配问题，将得到的离散松弛解转化为原问题的合法解，从而为原问题的最优值提供了一个上界；本发明总结了不同大小的竖直或水平模板成本的一般规则，并构建一个加权冲突分组图；基于加权冲突分组图，提出了一个新的整数线性规划mtadt问题，这不等于mtadt问题，但提供了mtadt问题的最优值的下界；此外，引入了一些有效的不等式来减掉一些不好的解，并获得更好的下界；本发明方法提出了一种模板分配方法，将松弛解转化为mtadt问题的可行解，并提供了mtadt问题最优值的上界；根据得到的下界和上界，可以评价实验结果的质量；特别是，如果上界等于下界，那么得到mtadt问题的最优解。

附图说明

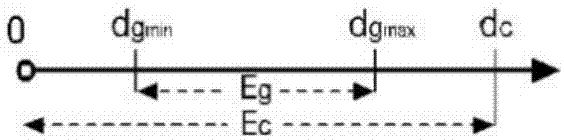
图1为冲突间隔和分组间距。

图2为冲突分组图的构建。

图3为不同模板的总的边成本。

图4为角不兼容性和三角边；其中，4(a)为加权冲突分组图；4(b)解决问题p2得到的解；4(c)新的加权冲突分组图；4(d)解决问题得到的解。

图5为具有角不兼容性的结构；其中，5(a)“l”形；5(b)“t”形；5(c)“z”形；5(d)“+”形。

图6为布局图的模板设计；其中，6(a)布局图；6(b)、6(c)两个模板设计结果。

具体实施方式

本发明提供了一种dsa通孔层三重模式分解的离散松弛法，包括如下步骤：

步骤s1、构造一个加权冲突分组图，其中引入负权重的边，然后提出一个基于掩模板分配的离散松弛问题；

步骤s2、用整数线性规划ilp公式来求解离散松弛问题，求得该离散松弛问题最优值的下界；

步骤s3、为了改善下界，引入有效的不等式来修正离散松弛解；

步骤s4、通过求解布局图上的模板分配问题，将得到的离散松弛解转化为dsa的三重模式的掩模板和模板设计问题合法解，从而为dsa的三重模式的掩模板和模板设计问题的最优值提供了一个上界。

在冲突分组图cgg中，由冲突边连接的两个通孔应分配给不同的掩模板，或者由mtadt的模板分组；为了减少使用掩模板的冲突和总成本，需确定通孔、冲突边是否应分组，此处通过加权来区分冲突边，然后构造加权冲突分组图wcgg；为处理分组，引入一个负权重的边，具体定义如下：

令通孔i和j之间的边eij∈e的加权规则设置为

其中，e表示加权冲突分组图wcgg中的所有边的集合；ec表示加权冲突分组图wcgg中的冲突边的集合；eg表示加权冲突分组图wcgg中的分组边的集合；en表示加权冲突分组图wcgg中的负边的集合；

根据上面的加权规则，可知：

2)如果通孔i1，i2被设计到相同的掩模板，并且则通孔之间存在冲突，并且边成本为1.0；

2)如果通孔i1，i2被设计到相同的掩模板，并且那么边成本是0.03；

3)如果将通孔i1，i2,i3设计给相同的掩模板，并且则边成本为0.05；

4)如果将通孔i1，i2，...，ik，k＝3,4设计给相同的掩模板，并且i1，i2，...，ik满足有k个洞的模板tk的条件；可以推断出k-1条分组边和k-2条负边，并且边的成本是0.03(k-1)-0.01(k-2)＝0.01(2k-1)。

为了解决离散松弛问题p1，将离散松弛问题p1转换为整数线性规划ilp问题p2等价于如下：

在上述公式中，xim是一个二元变量，表示为通孔i设计的掩模板；如果xim＝1，那么i被设计给掩模板m；cij是一个二元变量，用于表示通孔i和j之间是否产生冲突；

在整数线性规划ilp问题p2中，约束公式(2a)被用来决定在通孔i和j之间是否有冲突cij；即对于eij∈e，如果通孔i和j在同一个掩模板中，则cij＝1；约束公式(2b)用于为通孔i选择掩模板；

求解整数线性规划ilp问题p2可获得dsa的三重模式的掩模板和模板设计问题p0的一个下界。

为了避免cis中的通孔点被设计到相同的掩模板中，通过添加三角形边将加权冲突分组图wcgg修改为新的加权冲突分组图wcgg，并且将每个三角边的权重设计为w＝λ；然后，给整数线性规划ilp问题p2增加四种新的约束，并将新的问题称为

对于“l”形结构，如果将三个通孔i，i和k设计给相同的掩模板，则由于角不兼容而至少存在一个冲突；为了获得更好的解，为“l”形结构的通孔i，i和k添加有效不等式，以避免将三个通孔i，i和k设计给相同的掩模板；有效不等式为：

xim+xkm+xjm≤2+cij，m＝1，2，3，(3a)

而通孔k是一个角落通孔；约束公式(3a)用于限制，如果通孔i，j和k被设计到相同的掩模板，则三角形边的冲突变量eij∈et，具有cij＝1，其中et表示加权冲突分组图wcgg中的三角边的集合；

对于“t”形结构，如果四个通孔i，j，l和k被设计到相同的掩模板，则由于角不兼容而至少存在一个冲突；同样，为“t”形结构的四个通孔添加有效不等式：

xim+xkm+xjm≤2+cij+cjl，m＝1，2，3；(4a)

xjm+xkm+xlm≤2+cij+cjl，m＝1，2，3；(4b)

通孔k是一个角落通孔；如果三个通孔i，j和k或j，l和k或四个通孔被分配给相同的掩模板，则使用约束公式4(a)-4(b)来限制：至少一个三角形边eij和ejl的冲突变量等于1；

对于“z”形结构，如果将四个通孔i，j，l和k设计给相同的掩模板，则由于角不兼容而至少存在一个冲突；类似地，为“z”形状结构的四个通孔添加有效不等式：

xim+xkm+xjm≤2+cij+ckl，m＝1，2，3；(5a)

xjm+xkm+xlm≤2+cij+ckl，m＝1，2，3；(5b)

通孔k和j是角通孔；如果将三个通孔i，j和k或j，l和k或四个通孔设计给相同的掩模板，则使用约束公式5(a)-5(b)来限制：至少三角边eij和ekl的一个冲突变量等于1；

对于“+”形状结构，如果五个通孔i，i，l，h和k被设计到相同的掩模板，则由于角不兼容性而至少存在两个冲突；类似地，为“+”形状结构的五个通孔添加有效不等式：

xim+xkm+xjm≤2+cij+cjl，m＝1，2，3；(6a)

xjm+xkm+xlm≤2+cjl+clh，m＝1，2，3；(6b)

xlm+xkm+xhm≤2+clh+chi，m＝1，2，3；(6c)

xhm+xkm+xim≤2+chi+cij，m＝1，2，3；(6d)

通孔k是一个角通孔；如果将“l”形cis中的三个通孔或“t”形cis中的四个通孔设计给相同的掩模板，则使用约束公式6(a)-6(d)来限制，则至少三角边的一个冲突变量等于1；如果将“+”形cis中的五个通孔设计给相同的掩模板，则三角形边eij，ejl，elh和ehi中的两个冲突变量等于1。

所述步骤s4的实现方法为：假设sl是“l”形cis，i，j和k是sl的三个通孔点，k是角通孔，teij是三角边；令xl＝{xi1，xi2，xi3，xj1，xj2，xj3，xk1，xk2，xk3}；显然，xl是x的一部分；如果i，j是设计给不同的掩模板，为了最小化目标，那么三角边teij的冲突变量cij＝0；如果通孔k的掩模板与i和j的掩模板不同，则该等式表示问题在xl的值等于问题p0在处的值且等于0；如果k的掩模板与i和j的掩模板相同，比如说i，那么对于如果分组边geki由多孔模板指导，则否则在k和i之间会产生冲突，有无论如何，它保持

如果sl的所有通孔点i，j和k被设计到相同的掩模板，则约束公式(3a)将强制cij为1；一方面，另一方面，由于sl是“l”形cis，(1)如果在中，sl需要一个冲突和包含sl中的一条分组边的多孔模板，则sl的分解成本为(2)如果在中，sl需要两个冲突，则因此有

对于sl，有对于“t”形，“z”形和“+”形的cis，可以类似地证明，结论仍然成立；

因此，对于问题p0的最优解x⁰，以及从x⁰中通过省略模板设计而得到的x，保持因此问题仍然是问题p0的离散松弛问题；通过在软件包cplex中使用分支定界法来解决问题由于问题在大规模情况下难以解决，故而引入图剪枝技术来减小问题的规模。所述图剪枝技术包括：连通分支的计算，度数小于3的点的删除和2边连通分支的计算；度数小于3的点的删除技术将删除部分通孔；此外，对于2边连通分支的计算，如果顶点i和j通过桥连接并在掩模板设计阶段被设计到相同的掩模板中，然后在i和j之间产生一个冲突；可通过旋转2边连通分支的其中一个的颜色来消除冲突，使得i和j处于不同的掩模板；而且，无需考虑i和j的模板设计。

以下为本发明的具体实施例。

如果v的两个通孔点i和j之间的距离小于dc，那么它们之间存在冲突边eij∈ec；如果v的两个通孔点i和j之间的距离在dgmin和dgmax之间，而i和j在竖直或水平线上，则在它们之间存在一个分组边eij∈eg。显然

根据通孔之间的距离，将具有通孔的布局转换为冲突分组模式。这可以在o(kn)运行时间中实现，其中n是触点的数量，并且k是触点的最小冲突间隔dc内的触点的最大数量。图1说明了冲突间隔和分组间隔，冲突分组图结构的一个例子如图2(b)所示，其中所有的行是冲突边，虚线是分组边。

离散松弛是一种优化方法，它通过一些松弛技术将一个难以实现的最小化问题放松到一个更容易的问题上。松弛问题的最优解提供了原始问题最小值的下界。

如图2所示，在冲突分组图cgg中，由冲突边连接的两个通孔应设计给不同的掩模板，或者聚集在模板上形成mtadt问题。为了减少使用模板的冲突和总成本，需要确定哪些通孔应该先分组，哪些冲突边不能通过分组来消除。通过加权来区分冲突边，然后构造加权冲突分组图(wcgg)。

通孔i和j之间的边eij∈e的加权规则设置为

其中，e表示加权冲突分组图wcgg中的所有边的集合；ec表示加权冲突分组图wcgg中的冲突边的集合；eg表示加权冲突分组图wcgg中的分组边的集合；en表示加权冲突分组图wcgg中的负边的集合；

图2(c)示出了加权冲突分组图的例子。根据上面的加权规则，可以看到：

1.如果通孔i1，i2被设计到相同的掩模板，并且则通孔之间存在冲突，并且边成本为1.0；

2.如果通孔i1，i2被设计到相同的掩模板，并且那么边成本是0.03；

3.如果将通孔i1，i2,i3设计给相同的掩模板，并且则边成本为0.05；

4.如果将通孔i1，i2，...，ik，k＝3,4设计给相同的掩模板，并且i1，i2，...，ik满足模板tk条件。可以推断出那里k-1条分组边和k-2条负边，并且边的成本是0.03(k-1)-0.01(k-2)＝0.01(2k-1)。图3(a)-(c)和图3(e)示出了上述情况1-4的例子。

在加权冲突分组图上考虑以下问题p1：

设x0和x1分别是问题p0和p1的解空间。对于问题p0的任何解x⁰，每个通孔都被设计了一个掩模板和一个模板。但是，对于问题p1的任何解x¹，每个通孔都已设计了一个掩模板，但尚未设计一个模板。这意味着，对于任何x⁰∈x0，可以通过省略模板设计从x⁰得到解x¹∈x1。

假设x⁰∈x0通过省略模板设计变换到x¹∈x1，x0和x1分别是问题p0和p1的解空间，f0(x⁰)和f1(x¹)分别是问题p0和p1的目标函数。那么有f1(x¹)≤f0(x⁰)。

其中k是模板类型的数量，|c|是总冲突的数量。如果通孔i和j被设计到相同的掩模板，eij∈ec，并且i和j没有被设计给相同的模板，则i和j之间产生冲突，即cij＝1。|tk|是在x⁰中使用的k孔模板的数量，其中在相同的k孔模板中的通孔应该在相同的掩模板中，并且满足竖直或水平的k孔模板条件。

x⁰的成本包括冲突成本和模板成本。通过省略模板设计从x⁰中获得x¹。令e＝et∪ed，其中et是在x⁰的相同模板中的通孔i和j之间的边的集合。ed是在的不同模板中的通孔i和j之间的边的集合。所以

首先，对于通孔i和j在x⁰的同一个模板中，根据问题p1的权重设置，

最后的不等式是由于对k≥2成立。

其次，考虑通孔i和j在x⁰的不同模板中的成本。在这里，只考虑处于相同掩模板中的通孔点i和j之间的成本，因为如果i和j处于不同的掩模板中，则成本为0.令e′d为边eij∈ed的集合，并且i和j是在同一个掩模板中。设并且那么而且正好是冲突的数量|c|。然后

因此，对于任何x⁰∈x0，并且对于从x⁰中通过省略模板设计而获得的x¹∈x1，有

为了解决离散松弛问题p1，将问题p1转换为整数线性规划(ilp)问题p2等价于如下：

在上述公式中，xim是一个二元变量，它表示为通孔i设计的掩模板。如果xim＝1，那么i被设计给掩模板m。cij是一个二元变量，用于表示通孔i和j之间是否产生冲突。

在问题p2中，约束(2a)被用来决定在通孔i和j之间是否有冲突cij。也就是说，对于eij∈e，如果通孔i和j在同一个掩模板中，则cij＝1。约束(2b)用于为通孔i选择三个掩模板中的一个。

求解问题p2的离散松弛问题可以获得问题p0的一个下界。但是问题p2的下界与最优值之间的差距可能很大，得到的分解结果可能质量较差。所提出的离散松弛方法不仅用于寻找mtadt问题的下界，而且还用于获得mtadt问题的一个较好的解。因此通过加入一些有效的不等式来改进问题p2提供的下界。

在图4(a)的加权冲突分组图wcgg中，实线是冲突边，其权重分别为w＝1.0；而虚线是分组边，它们的权重分别为w＝0.03。图4(b)显示了问题p2的最优解x，其中两个冲突变量和等于1，问题p2的目标值为0.06。但是，在模板设计阶段，不能将通孔i1，i4和i5设计到相同的模板中。两个冲突分组边和中只有一个可以聚集到t2模板中，另一个会引起冲突，p0的总成本为因此，在离散松弛问题p2和问题p0差距的客观值为在下面，令

为了缩小差距，进一步改善问题p0解的质量，应该如图4(b)所示处理。把这个案例称为角不兼容(ci)。更为正式地说，角不兼容性就是，至少存在两个分组边和通孔k相关联则称为角通孔，并且至少两个包含k的分组边是正交的。由于角不兼容是不允许的，通过引起一些有效的不等式来排除本节中的角不兼容性。这项技术是增加一些额外的边，这些边被称为三角边，定义为：

三角边是图中的无向边。如果存在两个顶点i和j通过分组边连接到相同的顶点k，即eik∈eg，ejk∈eg，并且如果则eij被添加到该图中并被称为三角边。

在图5中，有四种类型的角不可兼性结构(cis)：i)如图5(a)所示的“l”形，和ii)如图5(b)所示的“t”形，和iii)如图5(c)所示的“z”形，和iv)如图5(d)所示，“+”形，和

为了避免cis中的通孔点被设计到相同的掩模板中，通过添加一些三角形边将wcgg修改为新的wcgg，并且将每个三角边的权重设计为w＝λ。然后，给问题p2增加四种新的约束，并将新的问题称为

对于“l”形结构，如果将三个通孔i，j和k设计给相同的掩模板，则由于角不兼容而至少存在一个冲突。为了获得更好的解，为“l”形结构的通孔i，j和k添加一些新的约束，以避免将三个通孔i，j和k设计给相同的掩模板。这些约束是：

xim+xkm+xjm≤2+cij，m＝1，2，3，(3a)

而通孔k是一个角落通孔。约束(3a)用于限制，如果通孔i，j和k被设计到相同的掩模板，则三角边的冲突变量eij∈et具有cij＝1。

对于“t”形结构，如果四个通孔i，j，l和k被设计到相同的掩模板，则由于角不兼容而至少存在一个冲突。同样，为“t”形结构的四个通孔添加一些有效的不等式。这些约束是：

xim+xkm+xjm≤2+cij+cjl，m＝1，2，3；(4a)

xjm+xkm+xlm≤2+cij+cjl，m＝1，2，3；(4b)

通孔k是一个角通孔。如果三个通孔i，j和k(或j，l和k)或四个通孔被设计给相同的掩模板，则使用约束4(a)-4(b)来限制：至少三角边eij和ejl的一个冲突变量等于1。

对于“z”形结构，如果将四个通孔i，j，l和k设计给相同的掩模板，则由于角不兼容而至少存在一个冲突。类似地，为“z”形状结构的四个通孔添加一些有效的不等式。这些约束是：

xim+xkm+xjm≤2+cij+ckl，m＝1，2，3；(5a)

xjm+xkm+xlm≤2+cij+ckl，m＝1，2，3；(5b)

其中通孔k和j是角通孔。如果将三个通孔i，j和k(或j，l和k)或四个通孔设计给相同的掩模板，则使用约束5(a)-5(b)来限制：至少三角边eij和ekl的一个冲突变量等于1。

对于“+”形状结构，如果五个通孔i，j，l，h和k被设计到相同的掩模板，则由于角不兼容性而至少存在两个冲突。类似地，为“+”形状结构的五个通孔添加一些有效的不等式。这些约束是：

xim+xkm+xjm≤2+cij+cjl，m＝1，2，3；(6a)

xjm+xkm+xlm≤2+cjl+clh，m＝1，2，3；(6b)

xlm+xkm+xhm≤2+clh+chi，m＝1，2，3；(6c)

xhm+xkm+xim≤2+chi+cij，m＝1，2，3；(6d)

通孔k是一个角通孔。如果将“l”形cis中的三个通孔或“t”形cis中的四个通孔设计给相同的掩模板，则使用约束6(a)-6(d)来限制，则至少三角边的一个冲突变量等于1。如果将“+”形cis中的五个通孔设计给相同的掩模板，则三角形边eij，ejl，elh和ehi中的两个冲突变量等于1。

实际上，根据实验，“t”形，“z”形和“+”形cis的数量是非常小的。在添加cis约束之后，图4(b)中的结构的新wcgg被构造为图4(c)。然后通过求解p2⁺问题，可以得到一个离散的松弛解，如图4(d)，而不是图4(b)。

问题仍然是问题p0的离散松弛。

证明如下：假设f2和f0分别是问题p2和p0的目标函数。假设x⁰是问题p0的最优解，并且x从x⁰中通过省略模板设计而获得，则x分别是问题和p2的解。问题和p2之间的差异是三种cis类型的三角边。分析一下这个成本问题中的三种cis类型。

假设sl是“l”形cis，i，j和k是sl的三个通孔点，k是角通孔，teij是三角边。令xl＝{xi1，xi2，xi3，xj1，xj2，xj3，xk1，xk2，xk3}。显然，xl是x的一部分。如果i，j是设计给不同的掩模板，为了最小化目标，那么三角边teij的冲突变量cij＝0。如果通孔k的掩模板与i和j的掩模板不同，则如果k的掩模板与i和j的掩模板相同，比如说i，那么对于如果分组边geki由多孔模板指导，则否则在k和i之间会产生冲突，有无论如何，它保持

如果sl的所有通孔点i，j和k被设计到相同的掩模板，则约束(3a)将强制cij为1。一方面，另一方面，由于sl是“l”形cis，(1)如果在中，sl需要一个冲突和包含sl中的一条分组边的多孔模板，则sl的分解成本为(2)如果在中，sl需要两个冲突，则因此有

因此，对于sl，有对于“t”形，“z”形和“+”形的cis，可以类似地证明，结论仍然成立。

因此，对于问题p0的最优解x⁰，以及从x⁰中通过省略模板设计而得到的x，保持因此仍然是问题p0的离散松弛。

在软件包cplex中使用分支定界法来解决问题由于问题在大规模情况下难以解决，引入一些图剪枝技术来减小问题的规模，使得使用分支定界法很容易解决。在本文中，所使用的图剪枝技术包括：连通分支的计算，度数小于3的点的删除和2边连通分支的计算。度数小于3的点的删除技术将删除一些通孔。由于这些删除的通孔可以很容易地设计给模板且没有任何设计的成本，在模板设计阶段后处理。此外，对于2边连通分支的计算，如果顶点i和j通过桥连接并在掩模板设计阶段被设计到相同的掩模板中，然后在i和j之间产生一个冲突。可以通过旋转2边连通分支的其中一个的颜色来消除冲突，使得i和j处于不同的掩模板。而且，不需要考虑i和j的模板设计。

通过求解问题得到问题p0的离散松弛解之后，必须决定离散松弛解的模板设计。问题的解将初始布局(删除的通孔点除外)分成三个掩模板，得到三个分解的布局l1，l2，l3。那么应该考虑每个分解布局lm(m＝1,2,3)的模板设计，描述如下：

每个分解掩模板的模板设计

给出：一个分解的通孔布局，一系列竖直和水平的模板。

查找：通孔的模板设计，通过可用的多孔模板对一些通孔进行分组。

约束：每个通孔仅设计给其中一个模板。

目标：|c|+β·tcoht最小化，其中|c|是冲突的数量，而tcoht是所用模板的总成本。

对于每个分解的布局lm(m＝1，2，3)，生成布局图lgm，并考虑lgm上的模板设计问题。lgm的定义是：

定义(布局图):布局lm的布局图是一个图lgm(cm，ecm)，其中cm是分解布局lm中的通孔集，ecm是冲突分组图cgg(v，ec)的冲突边的集合，它们是竖直或水平，只能连接lm中的通孔。

让egm是lm中任何两个通孔之间的分组边的集合。很明显，首先计算布局图lgm(m＝1，2，3)的所有连通分支cc，然后逐个处理每个连通分支。由于ecm中的边可以是竖直的或水平的，因此lgm(cm，ecm)的每个连接分支中所考虑的通孔都竖直或水平排列。图6(a)表示具有12个通孔的连接分支的布局图lgm，其中虚线是分组边egm。

在cc中存在一些角通孔。角通孔可以是下述三种类型之一：i)属于“+”形结构的角通孔；ii)属于“t”形结构的角通孔；iii)属于“l”形结构的角通孔。在图6(a)中，i5是属于“+”形结构的角通孔，i7是属于“t”形结构的角通孔，并且i12是属于“l”形结构的角通孔。

对于lgm中的每个孤立点，将其设计给单孔模板。对于没有角通孔的每个cc，cc中的所有通孔竖直或水平排列，并且将这些通孔首先贪婪地设计给最多孔的模板。否则，对于lgm的其他复杂cc，考虑启发式设计方法如下。

请注意，一旦cc中的所有角通孔都被设计到竖直或水平模板中，则其他通孔可以在没有角通孔的情况下用该方法对cc进行最佳设计。因此，为了获得复杂cc的最佳模板设计，只需要决定角通孔i是设计给竖直还是水平模板。二元变量yi用于表示i是否被设计给竖直模板。也就是说，yi＝0表示i被设计给一个竖直模板；yi＝1表示i被设计到一个水平模板。

图6(b)和(c)显示了图6(a)的两个模板设计结果。当y是(0,1,0)时，结果如图6(b)并且当y是(0,0,1)时，结果如图6(c)并且

以上是本发明的较佳实施例，凡依本发明技术方案所作的改变，所产生的功能作用未超出本发明技术方案的范围时，均属于本发明的保护范围。