一种水闸闸基覆盖层渗透系数反演分析方法与流程

本发明属于水闸渗压监测技术领域，涉及一种水闸闸基覆盖层渗透系数反演分析方法。

背景技术

水闸是修建在河道上的一种低水头挡水建筑物，可用于发电、防洪、灌溉或供水等，是国民经济重要的基础设施之一。在中国西南山区修建了较多的水闸，其中大多数水闸建在透水性强、渗透稳定性差的覆盖层地基上。闸基渗流性态是影响水闸运行安全的关键因素之一，通常在闸基中埋设渗压计进行渗流监测。渗压监测数据可以真实反映闸基渗流性态，但缺点是测点数量有限，只能观测局部渗流情况。采用有限元法进行渗流分析，可以比较真实地模拟闸基的材料组成、各种材料的渗流特性、防渗设施和渗流边界条件等，得到整个计算模型区域内的渗流场，因此，有限元法可以更加全面地分析闸基渗流状态。闸基覆盖层渗透系数的取值对闸基渗流的计算结果影响较大，如果渗透系数取值不合理，则渗流计算结果与实际渗流情况会存在较大差异。根据渗压监测数据率定闸基覆盖层渗透系数(即渗透系数的反演分析)，然后采用率定后的渗透系数进行渗流有限元计算，可使结果更接近实际情况。

目前，水闸闸基覆盖层渗透系数反演分析采用的方法是：在闸基覆盖层渗透系数的可能取值范围内采用某种优化方法(或优化软件)搜索渗透系数的最优值，使采用有限元计算的渗压值和渗压监测值的总体差值最小。渗透系数的每一次搜索，都要进行一次渗流有限元计算。因此，该方法需要进行大量有限元计算，效率较低。

技术实现要素：

本发明解决的问题在于提供一种水闸闸基覆盖层渗透系数反演分析方法，通过构造渗压计算值的响应面方程，代替耗时的有限元计算，减少计算量，提高渗透系数反演分析的效率。

本发明是通过以下技术方案来实现：

一种水闸闸基覆盖层渗透系数反演分析方法，包括以下操作：

1)根据水闸闸基的地质剖面图和闸基防渗布置图，建立闸基平面渗流有限元计算模型；并根据渗压计的埋设位置，在有限元模型中相应位置布置结点；

2)根据水闸闸基的覆盖层地层岩性及其分布，明确覆盖层材料种类以进行其渗透系数反演分析；

3)通过正交试验设计对反演分析的不同材料的渗透系数进行组合；

4)利用有限元软件ansys热分析模块进行闸基渗流分析，根据不同的渗透系数组合，计算得到闸基的整体渗流情况，及相应于渗压计埋设处的节点位置渗压；

5)构造渗压计算值的响应面方程如下：

式中，为渗压计算值，是的函数，为覆盖层材料渗透系数的组合，用向量表示；ki和kj为第i和第j种材料的渗透系数；ai、bij、ci和c为响应面方程的系数；n为需要率定渗透系数的材料数量；

根据不同渗透系数组合对应的渗压计算值，通过回归分析确定渗压计算值的响应面方程(1)的系数ai、bij、ci和c；

6)利用渗压计算值的响应面方程(1)和由渗压计测得的渗压实测值，建立如下渗透系数反演分析的目标函数：

式中，为目标函数，是的函数；为第k种工况下第i个测点的渗压计算值的响应面方程，为相应的渗压实测值；和分别为第j种材料渗透系数的上、下限；m、n、l分别为工况数、需要率定渗透系数的材料数量和测点数；

7)采用lingo软件搜索使(2)式目标函数值最小且(3)式成立的渗透系数组合，反演分析结束。

所述的有限元计算模型是利用ansys软件来建立的，该有限元计算模型包含闸底板、下游护坦、闸基防渗结构、闸基覆盖层及下部岩床；护坦中的排水孔通过增大相应位置处单元的渗透系数的方式模拟；

模型自闸底板上游端向上游延伸至少50m，自下游护坦末端向下游延伸至少50m，自覆盖层底部向下延伸至少30m。

在利用ansys软件的热分析模块计算闸基渗流分析时：采用plane55热分析单元离散有限元模型，模型上下游边界及底部边界为对应用绝热边界模拟的不透水边界，水头用温度模拟，模型顶部边界水头取相应上、下游水头；水头及边界条件不变，只改变覆盖层材料的渗透系数。

在通过正交试验设计进行渗透系数的组合时，每种材料的渗透系数取3个值μ、μ(1-kδ)、μ(1+kδ)，其中μ为渗透系数的均值，δ为渗透系数的变异系数，k为系数，然后根据正交试验表，对所选材料的所有渗透系数进行组合。

与现有技术相比，本发明具有以下有益的技术效果：

本发明提供的水闸闸基覆盖层渗透系数反演分析方法，是基于响应面法进行的反演分析方法，通过构造渗压计算值的响应面方程，代替耗时的有限元计算，减少计算量，提高渗透系数反演分析的效率。在此基础上，本发明通过建立渗透系数反演分析的目标函数，而建立渗透系数反演分析的目标函数需要采用渗压的计算值和实测值，求解一个以渗透系数为未知变量的优化问题。若采用有限元法计算渗压，既耗时又无法建立显示表达的目标函数，给之后的优化问题的求解造成困难。本发明采用渗压计算值的响应面方程(即以渗压计算值为因变量和需要率定的渗透系数为自变量的函数)代替有限元计算，可以建立显示表达的目标函数，提高参数反演分析的效率。

进一步的，渗透系数的反演分析就是在各种材料的渗透系数的上、下限范围内搜寻一组渗透系数使式(2)表达的目标函数值最小。因此，渗透系数的反演分析可以转化为带约束条件的非线性规划问题。本发明利用lingo软件求解式(2)和式(3)表达的非线性规划问题。lingo软件在求解大型非线性规划问题方面具有编程简单、计算稳定可靠和求解迅速的优势。

附图说明

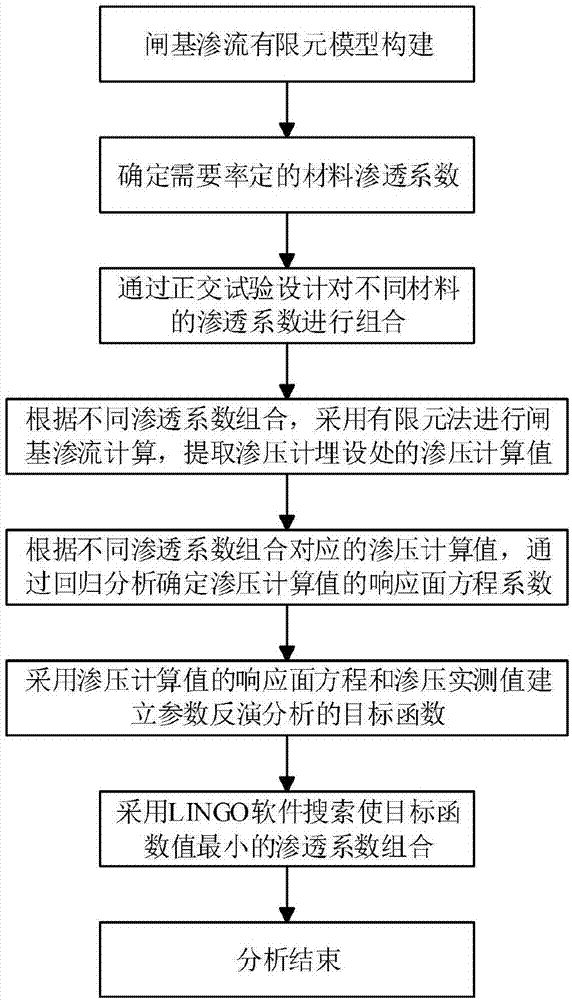
图1为本发明的水闸闸基覆盖层渗透系数反演分析方法的流程图

图2为正交试验设计示意图；

图3为拦河闸横河向剖面图；

图4为1#闸孔顺河向剖面图；

图5为2#闸孔顺河向剖面图；

图6为闸基渗压监测平面布置图；

图7为1#闸孔的闸基有限元模型网格；

图8为2#闸孔的闸基有限元模型网格；

图9为测点处渗压计算值与监测值比较(汛期)；

图10为测点处渗压计算值与监测值比较(枯期)。

具体实施方式

下面结合具体的实施例对本发明做进一步的详细说明，所述是对本发明的解释而不是限定。

本发明提供一种水闸闸基覆盖层渗透系数反演分析方法，包括以下操作：

1)根据水闸闸基的地质剖面图和闸基防渗布置图，建立闸基平面渗流有限元计算模型；并根据渗压计的埋设位置，在有限元模型中相应位置布置结点；

具体的，根据水闸闸基的地质剖面图和闸基防渗布置图，利用ansys软件建立闸基平面渗流有限元计算模型。模型应包含闸底板、下游护坦(含排水孔)、闸基防渗结构(如上游铺盖、混凝土防渗墙)、闸基覆盖层及下部岩床。护坦中的排水孔通过增大相应位置处单元的渗透系数的方式模拟。模型应自闸底板上游端向上游延伸至少50m，自下游护坦末端向下游延伸至少50m，自覆盖层底部向下延伸至少30m。为了对比计算渗压和实测渗压，根据渗压计的埋设位置，在有限元模型中相应位置布置结点。

2)根据水闸闸基的覆盖层地层岩性及其分布，明确覆盖层材料种类以进行其渗透系数反演分析；

3)通过正交试验设计对反演分析的不同材料的渗透系数进行组合；

采用正交试验设计进行渗透系数的组合。以三种材料的渗透系数的组合为例进行说明。每种材料的渗透系数取3个值，即μ、μ(1-kδ)、μ(1+kδ)，其中μ为渗透系数的均值，δ为渗透系数的变异系数，k为系数。然后根据正交试验表，对3种材料的9个渗透系数进行组合，得到9个试验点，如图1中立方体网格中的黑色圆点所示。由图2可见，立方体网格共有6个平面，每个平面上都有三个试验点，每条直线上都有1个试验点，并且这些试验点是均匀分散的，能很好地代表大量试验点的情况。

4)利用有限元软件ansys热分析模块进行闸基渗流分析，根据不同的渗透系数组合，计算得到闸基的整体渗流情况，及相应于渗压计埋设处的节点位置渗压；

由于渗流分析和热分析的基本方程相似(渗流分析方程中的渗流水头和材料渗透系数分别对应于热分析方程中的温度和材料导热系数)，因此，可以采用ansys软件的热分析模块计算闸基渗流。采用plane55热分析单元离散有限元模型。模型上下游边界及底部边界为不透水边界(用绝热边界模拟)，模型顶部边界水头取相应上、下游水头(水头用温度模拟)。

5)构造渗压计算值的响应面方程如下：

式中，为渗压计算值，是的函数，为覆盖层材料渗透系数的组合，用向量表示；ki和kj为第i和第j种材料的渗透系数；ai、bij、ci和c为响应面方程的系数；n为需要率定渗透系数的材料数量；

根据不同渗透系数组合对应的渗压计算值，通过回归分析确定渗压计算值的响应面方程(1)的系数ai、bij、ci和c；

6)利用渗压计算值的响应面方程(1)和由渗压计测得的渗压实测值，建立如下渗透系数反演分析的目标函数：

式中，为目标函数，是的函数；为第k种工况下第i个测点的渗压计算值的响应面方程，为相应的渗压实测值；和分别为第j种材料渗透系数的上、下限；m、n、l分别为工况数、需要率定渗透系数的材料数量和测点数；

7)采用lingo软件搜索使(2)式目标函数值最小且(3)式成立的渗透系数组合，反演分析结束。

下面给出具体的实施例。

某水闸位于中国四川省境内的岷江干流上，该水闸从左岸至右岸由取水口拦污栅闸、拦河闸、挡水坝等建筑物组成。拦河闸横河向长度为156m，顺河向长度为25m，最大闸高21.4m，设有6孔泄洪冲沙闸。闸基覆盖层最大深度45m，采用上游混凝土铺盖和悬挂式防渗墙防渗，防渗墙位于闸室上游20m，厚度0.7m，最大深度27m。闸室上游铺盖长75m～95m，闸室下游护坦长56m。闸址处两岸岸坡较缓，临河坡高300m～500m，河谷较开阔，河床宽80m～100m。闸址处河床覆盖层由漂卵石层和砂壤土层及卵砾石层组成，厚度约40m～62m。拦河闸横河向与顺河向剖面如图3～图5所示。为了监测闸基渗压，以及上游铺盖和悬挂式防渗墙的防渗效果，在防渗墙后沿坝轴线方向钻孔埋设了两排渗压计，其中上游侧布置了5支渗压计(编号为up1～up5)，下游侧布置了3支渗压计(编号为up6～up8)，总共8支渗压计。闸基渗流监测布置见图6。

对该水闸闸基覆盖层材料的渗透系数进行反演分析，具体步骤如下：

(1)根据闸基地质剖面图，采用ansys软件建立1#闸孔和2#闸孔的闸基平面渗流有限元模型。如图7和图8所示。为了对比计算渗压和实测渗压，根据渗压计的埋设位置，在有限元模型中相应位置布置结点(1#闸孔闸基中的渗压计为up2和up6，2#闸孔闸基中的渗压计为up3和up7)。

(2)由该闸基覆盖层地层岩性及其分布可知，该闸基覆盖层由漂卵石层、卵砾石层和砂壤土层组成，其渗透系数分别为k1、k2和k3，对这三种材料的渗透系数进行反演分析。

(3)渗压计算值的响应面方程为：

式中，为渗压计算值，是材料渗透系数的函数；ki和kj为第i和第j种材料的渗透系数；ai、bij、ci和c为响应面方程的系数。

(4)渗压计算值的响应面方程(1)中共有10个系数，采用回归分析确定这些系数需要10个以上的试验点。因此，进行两次正交试验设计，共得到18个试验点。第一次正交试验设计每种材料的渗透系数取μ、μ(1-δ)、μ(1+δ)3个值，第二次取μ、μ(1-3δ)、μ(1+3δ)3个值，其中μ采用渗透系数的设计值(见表1)，δ取0.3。采用spss软件的正交试验设计模块对漂卵石、卵砾石和砂壤土三种材料的渗透系数进行组合，结果见表2。

(5)对表2中的每一组渗透系数，采用图7和图8所示的有限元模型进行汛期和枯期两种工况下的闸基渗流计算，提取up2、up3、up6和up7四个渗压计埋设处的渗压计算值，见表3。

(6)为了更精确计算出之后建立的目标函数，得出最优解，可增加响应面方程个数，根据表2和表3中的数据，利用spss软件的回归分析模块确定汛期和枯期工况下up2、up3、up6和up7四个测点处渗压计算值的响应面方程系数，得到以下8个响应面方程：

响应面方程系数可通过上述响应面方程来确认，如在响应面方程h(1)中，c＝939.355,a1＝0.056,a2＝0.167,a3＝0.18,b1＝0.004,b2＝0.003,b3＝0.014,c1＝0.002,c2＝0.01,c3＝0.017.

由表4可知，在以上8个响应面方程的回归分析中，其复相关系数比较大，另外，将用已求得的响应面方程求得的渗压值与实测渗压值相比较，其最大误差小于0.279％。因此，响应面方程拟合精度较高，可以采用以上响应面方程计算up2、up3、up6和up7四个测点处的渗压值。

(7)利用渗压计算值的响应面方程和渗压的实测值(从案例获取)，建立如下渗透系数反演分析的目标函数：

μj(1-3δ)≤kj≤μj(1+3δ),j＝1,2,3.(11)

式中，为目标函数，是渗透系数的函数；为第k种工况下第i个测点的渗压计算值的响应面方程，为相应的渗压实测值；μj为第j种材料渗透系数的设计值。

(8)采用lingo软件，通过lingo建模语言将式(10)和式(11)编译成对应的数学模型，进行优化问题求解，即搜索漂卵石、卵砾石和砂壤土渗透系数的最优组合，使目标函数值最小，求得的各材料渗透系数率定值见表一，即相较其设计值而言，得到了覆盖层各层材料渗透系数的最优组合情况。采用反演分析确定的覆盖层材料渗透系数进行闸基渗流计算，图9和图10显示了up2、up3、up6及up7四个测点处的渗压计算值和实测值。

可以看出，渗压的计算值和实测值比较接近，说明采用本发明所述的反演分析方法可以比较准确地确定闸基覆盖层材料的渗透系数。

表1材料渗透系数的设计值和率定值

表2闸基覆盖层材料渗透系数的正交试验设计结果

表3采用有限元计算的up2、up3、up6和up7四个测点处的渗压值(m)

表4响应面方程回归分析特征值统计

以上给出的实施例是实现本发明较优的例子，本发明不限于上述实施例。本领域的技术人员根据本发明技术方案的技术特征所做出的任何非本质的添加、替换，均属于本发明的保护范围。