基于双重最小二乘支持向量机的固化热过程时空建模方法与流程

本发明涉及固化热过程建模领域，尤其涉及基于双重最小二乘支持向量机的固化热过程时空建模方法。

背景技术：

在芯片封装过程中，固化过程是其中最重要的一个过程之一。芯片固化质量的好坏，直接影响最终成品的质量以及使用寿命。而固化过程所使用的设备即为芯片固化炉。固化炉的内部有一个拱形的加热模块，它的作用是使得炉腔内的温度场保持一致。炉腔下端有一个冷却装置，它的作用是使得炉腔内的温度在上下方向上形成一个温度梯度，这样可以满足芯片在不同固化阶段所需的不同温度的要求。由于固化过程的边界条件非常复杂以及内部未知扰动的影响，固化过程的精确偏微分方程描述很难获得。固化炉属于分布式参数系统(dps)，虽然根据热传递规律，可以大致获得固化炉的偏微分方程结构，但是仍有许多模型参数无法获得。由于芯片固化质量对温度的分布要求非常高，因此基于数据的时空分布模型对于固化过程的温度管理具有非常重要的意义。

技术实现要素：

本发明的目的在于提出基于双重最小二乘支持向量机的固化热过程时空建模方法，建立芯片固化热过程模型，实现芯片固化炉在线温度监测和温度分布的在线估计，并且建模精度高。

为达此目的，本发明采用以下技术方案：

一种基于双重最小二乘支持向量机的固化热过程时空建模方法：

步骤一，搭建芯片固化炉温度控制平台，在芯片固化炉的炉腔底部安装引线框架，在引线框架的上表面均匀布置多个热电偶传感器，并由上位机采集所有热电偶传感器的温度数据，还在引线框架的上方均匀布置多个加热器，每个加热器由一个脉宽调制信号和一个功率放大器提供输入信号使芯片固化炉进行固化工作；

步骤二，上位机统计所有热电偶传感器的温度数据，得到芯片固化炉在固化工作状态下的温度分布随时间变化的时空数据，并将所述时空数据定义为：

{t(x，y，z，t)|x＝1，...，nx，y＝1，...，ny，z＝1，...，nz，t＝1，...，l}

其中，nx表示时空数据在x方向的数据点个数，ny表示时空数据在y方向的数据点个数，nz表示时空数据在z方向的数据点个数，l为时间长度；

步骤三，上位机通过pca算法(即主成分分析算法)学习一组表征空间非线性特征的空间基函数从而将步骤二采集到的时空数据t(x，y，z，t)解耦为：

其中，ai(t)为时空数据t(x，y，z，t)的常微分方程模型，n为常微分方程模型的阶数；

步骤四，上位机使用伽辽金方法将常微分方程模型ai(t)分解成两个独立的非线性模块gⁱ(·)和hⁱ(·)：ai(t)＝gⁱ(ai(t-1))+hⁱ(u(t-1))；

步骤五，上位机使用两个最小二乘支持向量机(ls-svm)串联构成双重ls-svm模型来逼近非线性模块gⁱ(·)和hⁱ(·)，并且通过ls-svm算法辨识非线性模块gⁱ(·)和hⁱ(·)的参数；

步骤六，上位机通过整合所述空间基函数和所述常微分方程模型，时空合成获得芯片固化炉1在固化工作状态下的温度时空分布模型。

优选地，所述步骤三中，上位机通过pca算法学习一组表征空间非线性特征的空间基函数具体为：

首先，定义时空数据t(x，y，z，t)的统计平均值为定义h1(x)和h2(x)在空间域ω的内积为(h1(x)，h2(x))＝∫ωh1(x)h2(x)dx；

接着，将时空数据t(x，y，z，t)和空间基函数的内积最大化：

subjectto(φi(·)，φi(·))＝1，φi(·)∈l²(ω)，i＝1，...，n；

构造拉格朗日函数：

其中，x为坐标(x，y，z)，极值的必要条件是函数导数对于所有变化为零：

并利用任意函数ψ(x)将条件简化为：

其中，r(x，ξ)＝<t(x，t)t(ξ，t)>是对称和正定的空间两点相关函数，从而将条件转化为以下特征值问题：

cδi＝λiδi，

其中，ctk是时间两点矩阵：

δi＝[δ1i，δ2i，...，δli]^t是第i个特征向量；

然后，通过求解cδi＝λiδi产生特征向量δ1，δ2，...，δl及其相应的特征值λ1，λ2，...，λl，和通过获得空间基函数；

最后，把特征值按照从大到小的顺序排列：λ1＞λ2＞...＞λl，其中前n个最大特征值和的占比为：

选取ratio≥0.99对应的值n作为空间基函数的阶数。

优选地，所述步骤四具体为：

首先，定义时空数据t(x，y，z，t)的方程残差为：

其中，c为比热系数(j/kg℃)，q＝q(x，y，z，t)是热源，是拉普拉斯算子，k1＝k0/ρoc是常数，k0和ρ0是工作点周围的标称值；

使用伽辽金方法将方程残差最小化，使(r，φi)＝0；从而得到：

其中，

ω域的范围是(0≤x≤x0，0≤y≤y0，0≤z≤z0)，

忽略常微分方程模型之间的耦合效应，上式简化为：

其中δt是离散化的采样间隔；

然后，定义非线性函数：

从而将常微分方程模型ai(t)分解成两个独立的非线性模块gⁱ(·)和hⁱ(·)：ai(t)＝gⁱ(ai(t-1))+hⁱ(u(t-1))。

优选地，双重ls-svm模型来逼近非线性模块gⁱ(·)和hⁱ(·)具体为：

首先，定义正交投影算子p，以从时空输出中获得时间系数：

其中，φ＝[φ1，...，φn]^t；

由于空间基函数φi(i＝1，...，∞)是单位正交的，因此时间系数为：

a(t)＝[a1(t)，...ai(t)，...，an(t)]^t；

然后，上位机使用一个最小二乘支持向量机逼近非线性模块gⁱ(·)，同时使用另一个最小二乘支持向量机逼近非线性模块hⁱ(·)，即：

从而常微分方程模型ai(t)为：

其中，和是映射函数，和分别是映射函数和的权重，和是相应的偏差项。

优选地，通过ls-svm算法辨识非线性模块gⁱ(·)和hⁱ(·)的映射函数及其权重和偏差项：

首先，基于最小二乘支持向量机原理，对常微分方程模型ai(t)优化为：

其中，c是近似精度和模型复杂度之间折衷的正则化常数，优化的约束条件是：

然后，构造拉格朗日函数：

优化拉格朗日函数的条件为：

消除和e(t)之后，将优化拉格朗日函数的条件转换为以下矩阵：

其中，

1l-1＝[1，...，1]^t，ai＝[ai(2)，...，ai(l)]^t；

根据mercer定理，内积和可以用核函数k(v1，v2)来定义，其中v1和v2是两个任意变量，核函数k(v1，v2)选用径向基核函数：其中σ表示核宽度，

当核函数k(v1，v2)给定后，双重ls-svm模型变为：

其中的未知参数βⁱ，γⁱ，由优化拉格朗日函数的条件矩阵获得。

优选地，所述步骤六的温度时空分布模型为：

优选地，还包括：步骤七，使用rademacher复杂度来度量所述温度时空分布模型的期望误差的上界，

若满足损失函数那么对于任意的δ∈(0，1)，都存在至少1-δ的概率使得所有的都满足：

其中：表示使用损失函数l的预期风险，

表示使用损失函数l的经验风险，

是与h和l有关的损失函数集合，

是关于的rademacher复杂性，m为测试样本的数量；

若那么模型函数集h的rademacher复杂性界限为：

从而若满足损失函数||βi||≤pi，那么对于任意的δ∈(0，1)，都存在至少1-δ的概率使得所有的都满足：

所述基于双重最小二乘支持向量机的固化热过程时空建模方法，用于在线预测和控制芯片固化炉的热过程，使用两个最小二乘支持向量机(ls-svm)串联构成双重ls-svm模型将专门为包含两个固有耦合非线性的dps设计，在两个耦合非线性的性能近似方面更有效，并且模型精度高。

附图说明

附图对本发明做进一步说明，但附图中的内容不构成对本发明的任何限制。

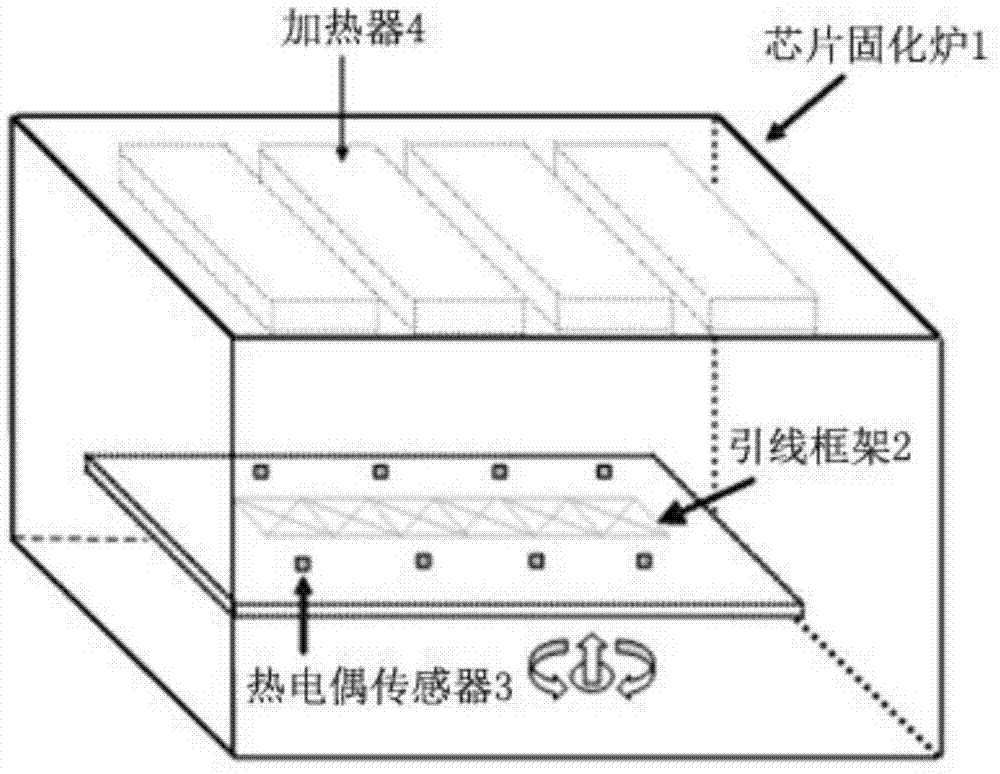
图1是本发明其中一个实施例的芯片固化炉结构示意图；

图2是本发明其中一个实施例的热电偶传感器分布图；

图3是本发明其中一个实施例的基于双重ls-svm的建模流程图；

图4是本发明其中一个实施例的第二个加热器h2的控制输入信号图；

图5是本发明其中一个实施例的从pca方法获得的第一个正交映射函数示意图；

图6是本发明其中一个实施例的从pca方法获得的第二个正交映射函数示意图；

图7是本发明其中一个实施例的pca建模方法在热电偶传感器s6处的性能图；

图8是本发明其中一个实施例的pca建模方法在热电偶传感器s11处的性能图；

图9是本发明其中一个实施例的预测的最后采样时刻的温度分布图；

图10是本发明其中一个实施例的热电偶传感器s6处的are比较图；

图11是本发明其中一个实施例的热电偶传感器s11处的are比较图。

其中：芯片固化炉1；引线框架2；热电偶传感器3、s1、s2、s3、s4、s5、s6、s7、s8、s9、s10、s11、s12、s13、s14、s15、s16；加热器4、h1、h2、h3、h4。

具体实施方式

下面结合附图并通过具体实施方式来进一步说明本发明的技术方案。

实施例一

本实施例的基于双重最小二乘支持向量机的固化热过程时空建模方法：

步骤一，搭建芯片固化炉温度控制平台，如图1、图2所示，在芯片固化炉1的炉腔底部安装引线框架2，在引线框架2的上表面均匀布置多个热电偶传感器3，并由上位机采集所有热电偶传感器3的温度数据，还在引线框架2的上方均匀布置多个加热器4，每个加热器4由一个脉宽调制信号和一个功率放大器提供输入信号使芯片固化炉1进行固化工作；

步骤二，如图3所示，上位机统计所有热电偶传感器3的温度数据，得到芯片固化炉1在固化工作状态下的温度分布随时间变化的时空数据，并将所述时空数据定义为：

{t(x，y，z，t)|x＝1，...，nx，y＝1，...，ny，z＝1，...，nz，t＝1，...，l}

其中，nx表示时空数据在x方向的数据点个数，ny表示时空数据在y方向的数据点个数，nz表示时空数据在z方向的数据点个数，l为时间长度；

步骤三，上位机通过pca算法(即主成分分析算法)学习一组表征空间非线性特征的空间基函数从而将步骤二采集到的时空数据t(x，y，z，t)解耦为：

其中，ai(t)为时空数据t(x，y，z，t)的常微分方程模型，n为常微分方程模型的阶数；

步骤四，上位机使用伽辽金方法将常微分方程模型ai(t)分解成两个独立的非线性模块gⁱ(·)和hⁱ(·)：ai(t)＝gⁱ(ai(t-1))+hⁱ(u(t-1))；

步骤五，上位机使用两个最小二乘支持向量机(ls-svm)串联构成双重ls-svm模型来逼近非线性模块gⁱ(·)和hⁱ(·)，并且通过ls-svm算法辨识非线性模块gⁱ(·)和hⁱ(·)的参数；

步骤六，上位机通过整合所述空间基函数和所述常微分方程模型，时空合成获得芯片固化炉1在固化工作状态下的温度时空分布模型。

根据芯片固化炉1的传热规律，芯片固化炉1的热过程一般表达式可以描述为：

其中(x，y，z)是空间坐标，t(x，y，z，t)表示在时间t和位置s＝(x，y，z)处的温度(单位℃)，(x，y，z)、x∈[0，x0]、y∈[0，y0]和z∈[0，z0]为空间坐标，c为比热系数(单位j/kg℃)，fc(t)和fr(t)分别为未知的对流和辐射非线性效应。q＝q(x，y，z，t)是热源，ρ和k分别是密度(单位kg/m³)和热导率(单位w/m℃)。

热导率k和密度ρ的取决于温度，并且可以表示为：

其中，k0和ρ0是工作点周围的标称值，和是t(x，y，z，t)的函数。

因此，可以转为以下形式：

其中，是拉普拉斯算子，k1＝k0/ρoc是常数；

是关于t的未知非线性函数。很明显，有两个非线性函数f(·)和q(·)，其中q(·)是关于u(t)的非线性函数。芯片固化炉1的热过程描述的偏微分方程具有无线维的特征，所以不能够直接用于在线预测和控制。因此为了实际应用，建立一个有限维的常微分方程描述的模型非常重要。

为了模拟这个系统，pca算法(即主成分分析算法)将首先用于将无限维模型转换为有限维模型；然后，一个新的双模型结构，即使用两个最小二乘支持向量机(ls-svm)串联构成双重ls-svm模型将专门为包含两个固有耦合非线性ai(t)＝gⁱ(ai(t-1))+hⁱ(u(t-1))的dps设计。

由于上述两种耦合非线性，将构造两个ls-svm模型来来更好的逼近原模型，每一个非线性模块都可以使用最小二乘支持向量机(ls-svm)的现有模型来分别近似。尽管一个ls-svm能够逼近任何非线性函数，但是，两个ls-svm比一个ls-svm在两个耦合非线性的性能近似方面更有效。

优选地，所述步骤三中，上位机通过pca算法学习一组表征空间非线性特征的空间基函数具体为：

首先，定义时空数据t(x，y，z，t)的统计平均值为定义h1(x)和h2(x)在空间域ω的内积为(h1(x)，h2(x))＝∫ωh1(x)h2(x)dx；

接着，将时空数据t(x，y，z，t)和空间基函数的内积最大化：

subjectto(φi(·)，φi(·))＝1，φi(·)∈l²(ω)，i＝1，...，n；

pca方法是从一组时空数据当中学习到空间基函数其中约束(φi(·)，φi(·))＝1是为了保证空间基函数的唯一性；

构造拉格朗日函数：

其中，x为坐标(x，y，z)，极值的必要条件是函数导数对于所有变化为零，r表示实数域：

并利用任意函数ψ(x)将条件简化为：

其中，r(x，ξ)＝<t(x，t)t(ξ，t)>是对称和正定的空间两点相关函数，从而将条件转化为以下特征值问题：

cδi＝λiδi，

其中，ctk是时间两点矩阵：

δi＝[δ1i，δ2i，...，δli]^t是第i个特征向量；

然后，通过求解cδi＝λiδi产生特征向量δ1，δ2，...，δl及其相应的特征值λ1，λ2，...，λl，和通过获得空间基函数；

最后，把特征值按照从大到小的顺序排列：λ1＞λ2＞...＞λl，其中前n个最大特征值和的占比为：

选取ratio≥0.99对应的值n作为空间基函数的阶数。

pca算法(即主成分分析算法)对实际系统的机理过程无需知道，只需要实验数据便可以得到原系统的数学模型。因此这种方法广泛的应用在dps建模应用当中。这种方法的建模思想主要是先对实验采集到的时空数据进行降维处理，通过求特征值特征向量问题来得到有限个数的空间基函数。然后使用传统的集中建模方法，比如神经网络(nn)，支持向量机(svm)，模糊模型等方法来确定低阶时序模型。最后通过时空重构，便可以获得原系统的基于数据的dps模型。

优选地，所述步骤四具体为：

首先，定义时空数据t(x，y，z，t)的方程残差为：

其中，c为比热系数(j/kg℃)，q＝q(x，y，z，t)是热源，是拉普拉斯算子，k1＝k0/ρoc是常数，k0和ρ0是工作点周围的标称值；

使用伽辽金方法将方程残差最小化，使(r，φi)＝0；从而得到：

其中，

ω域的范围是(0≤x≤x0，0≤y≤y0，0≤z≤z0)，

忽略常微分方程模型之间的耦合效应，上式简化为：

其中δt是离散化的采样间隔；

然后，定义非线性函数：

从而将常微分方程模型ai(t)分解成两个独立的非线性模块gⁱ(·)和hⁱ(·)：ai(t)＝gⁱ(ai(t-1))+hⁱ(u(t-1))。

将芯片固化炉1热过程的偏微分方程，进行时空变量分离并且使用伽辽金方法对其进行截断，最终获得的低阶名义模型可以近似成两个独立的非线性模块gⁱ(·)和hⁱ(·)。如果权重函数选择为空间基函数那么这种方法可以称为伽辽金方法。伽辽金方法的优点是残差与每一个空间基函数都是正交的，因此，最优解即为n个空间基函数由于这种方法最终只需确定空间基函数即可，所以具有简单有效的特点。

优选地，双重ls-svm模型来逼近非线性模块gⁱ(·)和hⁱ(·)具体为：

首先，由于测得的数据是时空分布数据，所以先对时空分布数据进行处理，以获得低阶模型输出数据，这样才能进一步辨识低阶模型参数，定义正交投影算子p，以从时空输出中获得时间系数：

其中，φ＝[φ1，...，φn]^t；

由于空间基函数φi(i＝1，...，∞)是单位正交的，因此时间系数为：

a(t)＝[a1(t)，...ai(t)，...，an(t)]^t；

然后，ls-svm方法是通过一个非线性映射函数把样本数据投影到更高维的特征空间，从而把一个非线性问题转化成高维特征空间的线性求解问题，上位机使用一个最小二乘支持向量机逼近非线性模块gⁱ(·)，同时使用另一个最小二乘支持向量机逼近非线性模块hⁱ(·)，即：

从而常微分方程模型ai(t)为：

其中，和是映射函数，和分别是映射函数和的权重，和是相应的偏差项。常微分方程模型ai(t)中所有的映射函数和相应的权重都需要辨识得到。

优选地，通过ls-svm算法辨识非线性模块gⁱ(·)和hⁱ(·)的映射函数及其权重和偏差项：

首先，基于最小二乘支持向量机原理，对常微分方程模型ai(t)优化为：

其中，c是近似精度和模型复杂度之间折衷的正则化常数，优化的约束条件是：

除了传统ls-svm对系统的约束之外，所述优化的约束条件中的两个约束条件是最小化每个非线性模块的近似误差；

然后，构造拉格朗日函数：

优化拉格朗日函数的条件为：

消除和e(t)之后，将优化拉格朗日函数的条件转换为以下矩阵：

其中，

1l-1＝[1，...，1]^t，ai＝[ai(2)，...，ai(l)]^t；

根据mercer定理，内积和可以用核函数k(v1，v2)来定义，其中v1和v2是两个任意变量，核函数k(v1，v2)选用径向基核函数：其中σ表示核宽度，

当核函数k(v1，v2)给定后，双重ls-svm模型变为：

其中的未知参数βⁱ，γⁱ，由优化拉格朗日函数的条件矩阵获得。mercer定理为任何半正定的函数都可以作为核函数。

优选地，步骤六的温度时空分布模型为：当低阶时序模型获得以后，便可重构得到一个时空分布模型。

优选地，还包括：步骤七，使用rademacher复杂度来度量所述温度时空分布模型的期望误差的上界，

若满足损失函数那么对于任意的δ∈(0，1)，都存在至少1-δ的概率使得所有的都满足：

其中：表示使用损失函数l的预期风险，

表示使用损失函数l的经验风险，

是与h和l有关的损失函数集合，

是关于的rademacher复杂性，m为测试样本的数量；

若那么模型函数集h的rademacher复杂性界限为：

从而若满足损失函数||βi||≤pi，那么对于任意的δ∈(0，1)，都存在至少1-δ的概率使得所有的都满足：

rademacher(拉德马赫)复杂度用于衡量一类实值函数的丰富性，并根据观察到的训练样本误差限制学习者的期望误差。与只能用于二元函数的vapnik-chervonenkis维度不同，rademacher的复杂度也可用于分析其他学习算法，如基于内核的算法。步骤七的具体过程为：通过使用rademacher复杂度的概念，可以导出以下定理：

定理1、假设该方法的预期风险小于经验风险和常数的总和，那么预期风险将是有界的。所以，所提出的方法是收敛的。

为了使用rademacher复杂性的概念来证明定理1，需要以下引理。

引理1、假设对于任何δ∈(0，1)都满足损失函数对于h满足的所有对于长度为m的样本，概率至少为1-δ；

其中：表示使用损失函数l的预期风险。

表示使用损失函数l的经验风险。

是与h和l有关的损失函数集合，

是关于的rademacher复杂性。

引理2、假设那么模型函数集h的rademacher复杂性界限为：

在学习过程中，定义损失函数如下：

假设平方损失函数是具有常数d＝2(a+||t||∞)的lipschitz函数(利普希茨函数)。那么损失函数集的rademacher复杂度可以表示如下：

根据引理1，对于任何δ∈(0，1)，长度为m的测试样本，概率至少为1-δ，对于h中的所有满足：

综上可知：

上式右边的最后两项等于一个常数。

实施例二

本实施例通过进行实时实验来验证所提出的建模方法。首先，搭建芯片固化炉温度控制平台，如图1所示，在芯片固化炉1的炉腔底部安装引线框架2，在引线框架2的上表面均匀布置16个相同规格的热电偶传感器3，热电偶传感器3的详细布置位置如图2所示。在引线框架2的上方均匀布置四个相同规格的加热器4，每个加热器4的功率为700w，热电偶传感器3均匀的布置在加热器4下方5mm的同一水平面上。每个加热器4由一个脉宽调制信号和一个功率放大器提供输入信号使芯片固化炉1进行固化工作；其中第二个加热器h2的控制输入信号如图4所示。

由上位机采集所有热电偶传感器3的温度数据。采样间隔为δt＝10s，每个热电偶传感器3都采集了2100组温度数据。其中热电偶传感器s1-s5，s7-s10，s12-s16的温度数据用来确定模型，热电偶传感器s6和s11的温度数据用来测试该模型在未训练位置处的性能表现。

然后，将基于pca的学习算法应用于这些温度数据，并使用pca算法构建3个正交映射函数。其中低维嵌入空间γik中相应特征值大小的第一和第二正交映射函数如图5、6所示。图7和图8显示了选定位置(s6和s11)的性能比较，其中估计性能(实数)非常接近实际系统(虚线)。显然，所提出的模型可以用来模拟炉腔中未经训练的位置的动态变化。对于空间域的性能，最后一个样本(第2100个)的比较如图9所示，其中开发的模型在空间和时间域都具有良好的模型性能。

在相同的实验条件下，分别使用单个ls-svm，双重ls-svm建立相应的低阶时序模型，并且与基于pca的空间基函数时空合成，获得各自的时空分布模型。

接下来比较两种方法的模型性能，，以下标准用于评估：

①空间归一化绝对误差(snae)：

②时间归一化绝对误差(tnae)：

③均方根误差(rmse)：

测试的性能指标tnae(x)如表1所示：

表1

为了进一步揭示本实施例双重ls-svm模型的优越性，所选位置(s6和s11)的比较指数are如图10、图11所示，其r-square如表2所示。

表2

说明本实施例提出的基于双重ls-svm的时空分布模型预测精度高。

以上结合具体实施例描述了本发明的技术原理。这些描述只是为了解释本发明的原理，而不能以任何方式解释为对本发明保护范围的限制。基于此处的解释，本领域的技术人员不需要付出创造性的劳动即可联想到本发明的其它具体实施方式，这些方式都将落入本发明的保护范围之内。