一种基于矩阵变量变分自编码器的图像处理方法与流程

本发明属于计算机视觉与机器学习领域，尤其涉及一种基于矩阵变量变分自编码器的图像处理方法。

背景技术

图像重构、去噪和补全是图像处理的重要内容，变分自编码器(variationalautoencoder,vae)因其能很好的建模图像数据的概率分布，所以广泛的应用于图像处理相关领域。vae通常由一个推理模型(编码器)和一个生成模型(解码器)组成，模型的目标函数包含两项：一是图像的重构误差，一般使用均方误差或交叉熵来度量；另一个是kullback-leibler(kl)散度，用来衡量基于推理模型学到的特征潜变量的后验与对特征假设的先验分布之间的相似度，相当于一个正则化项。

由于vae能够建模特征潜变量的统计分布，因此当在该分布中进行随机采样并通过解码器解码时，能够生成与原始数据类似的样本，因此可去除噪声或对缺失图像补全。但是目前的vae方法的一个缺陷：是建模向量变量的，当用于处理图像数据时，需要先将其数据进行向量化处理，一方面可能带来维度灾难，另一方面向量化的处理必然会破坏图像数据的空间结构，造成大量的局部空间信息的丢失。

技术实现要素：

本发明要解决的技术问题是，提供一种基于矩阵变量变分自编码器(matrix-variatevariationalautoencoder，mvvae)进行图像处理的方法，能够解决图像向量化处理破坏空间结构的问题，进而利于图像重构、去噪和补全。与传统vae不同的是，本方法用图像的固有表示形式-2d矩阵来描述模型的输入、隐层特征、潜变脸分布特征参数等，通过利用矩阵高斯分布的定义及相关性质推导新模型的目标函数的显式表达，然后利用随机梯度下降算法求解模型参数。在这个模型中，由于本发明涉及的建模过程都是面向矩阵变量的，因此能更好的建模图像数据的空间结构和统计信息，进而可以提升图像重构质量、更好去除噪声和图像补全。

附图说明

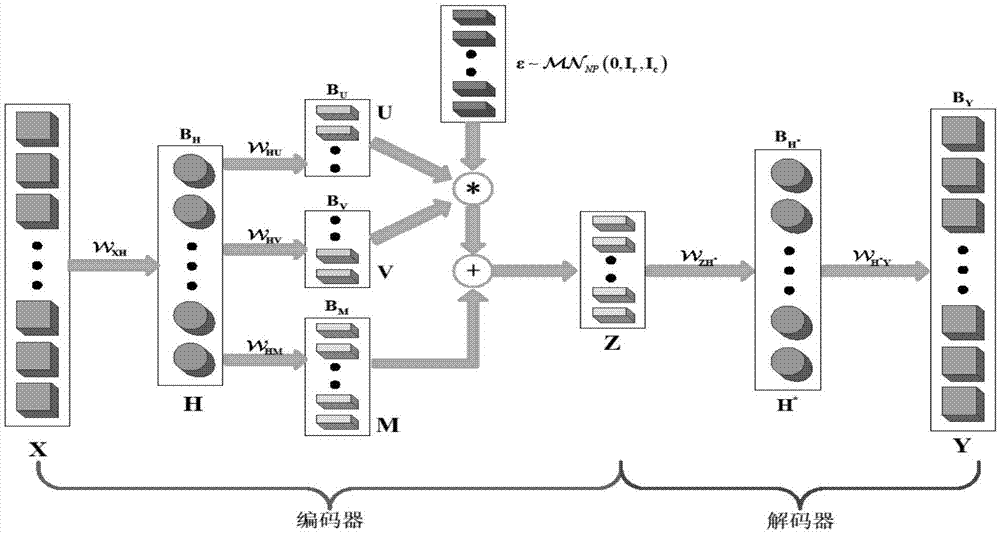
图1矩阵变量变分自编码器模型；

图2不同潜变量维度下mvvae和vae对mnist数据集重构效果的比较；图3不同隐变量维度下mvvae和vae对mnist数据集重构效果的比较；

图4使用vae模型和mvvae模型对图像进行去噪效果的对比；

图5对缺失图像进行补全效果对比。

具体实施方式

本发明提供一种基于矩阵变量变分自编码器(matrix-variatevariationalautoencoder，mvvae)进行图像处理的方法，

假设有n个独立同分布的图像集每个图像表示为即输入样本的大小为i×j的二维矩阵。本发明旨在建模图像集的统计分布logpθ(x)，进而有效的进行图像的重构、去噪和补全。对图像的建模过程是基于本发明所提出的mvvae网络，所以核心是建模该网络，训练得到网络模型的参数。

为实现上述目的，本发明采用如下的技术方案：

1.面向图像集分布建模的mvvae模型的定义

mvvae模型定义，如图1所示，

在该模型中是输入层矩阵变量，对应的是输入图像的矩阵表示，i和j分别代表输入图像数据的行列维度的大小。为隐藏层矩阵变量，对应的是基于模型提取的输入图像的特征，c和d分别代表隐藏层特征矩阵行列维度的大小。和分别为输入图像对应的潜变量的均值、行协方差和列协方，它们是对隐层特征h的进一步统计描述。为潜在矩阵变量，n和p分别代表潜在层矩阵行列维度的大小，z从特征h的统计分布中采样得到。同样地，解码器的矩阵变量重构它们的行和列维度分别与编码器特征h和输入图像矩阵变量x相对应。

矩阵变量变分自编码器模型中除潜变量层外，每一层都是基于多层感知机神经网络，编码器的参数为解码器的参数为这些参数是我们在模型训练过程中要求解的。

mvvae网络模型的目标函数定义如下：

假设有n个图像该模型假设每个样本x由一个未观测变量生成，θ为网络中生成模型的参数，并且该模型引入变分思想，即使用一个后验概率来近似潜在变量的真正后验分布pθ(z|x)，而近似的后验概率使用网络的推理模型来实现，为网络中推理模型的参数。则每个样本的边缘似然可以表示为：

通过上述变分推理，可以求出边缘似然logpθ(x)的紧致下界，它主要包含两项：第一项为重构误差；第二项为kl散度，衡量的是基于推理模型学到的特征潜变量的后验与对特征假设的先验分布之间的相似度，并且当近似的后验概率与真正的后验概率pθ(z|x)越相近，则变分下界与边缘似然logpθ(x)之间的差距越小。因此该模型是通过不断求解下界的极大化逼近近似对数似然函数极大化的算法。

2.mvvae模型的参数求解算法

从公式(1)可以看出，目标函数主要分为两项：第一项为重构误差。第二项为衡量的是基于推理模型学到的特征潜变量的后验与对特征假设的先验分布之间的相似度，相当于一个正则项。下面本发明从矩阵变量概率分布及性质定义出发，对这两项进行分别求解以给出显示的表示。

对进行求解。

假设mvvae模型中的潜在变量z的先验pθ(z)服从均值为o，协方差为单位阵的标准矩阵高斯分布，即：则近似的后验概率必然服从矩阵高斯分布，即:其中为模型中潜变量的均值，和分别为潜变量的行协方差和列协方差，特别地，m，u，v参数通过神经网络的编码器学习得到，如图1所示。

按照kl散度的定义，将展开,得：

根据矩阵高斯分布的性质，可得：

以及：

因此，公式(2)可以表示为：

其中，tr(·)表示矩阵的迹运算，|·|表示矩阵的行列式。

在矩阵高斯分布中约束行协方差u和列协方差v都为正定矩阵，根据正定矩阵的性质，可以进一步得到：

对进行求解。

在矩阵变量变分自编码器中编码器和解码器都是基于神经网络的，在本发明中使用最广泛应用的多层感知器(multi-layeredperceptrons,mlps)。该模型中重构误差的损失函数与ae类似，它有多种选择，主要依赖于输入数据的类型。

1)当输入样本图像是二值的，即输入层的每个神经元只能取0或1，那么编码器的输出一般假设其服从伯努利分布，则损失函数通常由负交叉熵来定义：

其中，xij为输入矩阵变量x的某一元素值，yij为相对应的输出矩阵变量y的一个元素值。首先，输入样本x经过编码器得到潜在变量z，然后潜在变量z经过解码器输出生成样本y,fσ(·)是一个sigmoid激活函数，是mlp的权重和偏置。

2)而对于实值的神经网络，即输入是任意图像，则编码器的输出一般假设其服从矩阵高斯分布，高斯分布参数为通过解码器输出的重构图像矩阵y的均值，和分别为重构图像y的行协方差和列协方差，m^*，u^*，v^*均是通过mlps学习得到，则用对数矩阵高斯分布定义损失函数,即：

这里，

以及

其中，是mlps的权重和偏置。

3.mvvae模型的训练

采用批处理方式来训练模型，具体的，将所有的训练图像集随机的分为若干子集，设置每个子集包含的样本个数为b，即每次输入图像集的大小为训练过程包括：首先定义网络每层节点维度的大小，并对网络权重进行随机初始化，然后使用随机梯度下降算法(sgd)对变分下界中的参数和θ进行联合的优化，直到模型收敛为止。下面介绍训练过程中所需的两种技巧。

1)重参数化技巧

在mvvae中一般使用随机梯度下降算法(sgd)对变分下界中的参数和θ进行联合的优化。而通过公式(1)可以看出，该变分下界的第一项为近似的后验概率条件下logpθ(x|z)的期望，与参数是有关的，因此参数的梯度是及其难求的。因此使用重参数化技巧来优化变分下界即引入一个随机噪声∈，并且ir,ic分别为行协方差和列协方差，两个协方差都为单位矩阵。则变分下界可以被重写为：

其中，l代表采样的次数，

2)权重分解技巧

在mvvae模型中，编码器每层之间的连接权重和解码器每层之间的连接权重都是四阶张量的形式，因此为了减少模型的自由度参数的数量从而降低模型复杂度和训练时间，借鉴tucker分解的思想，采用自定义张量分解的形式，对权重进行分解。如对于连接可见层x和隐层h的四阶张量的权重参数来说，通过定义两种新的矩阵和对连接权重进行分解，即：则隐层矩阵变量为：同样对于其它层之间的四阶张量连接权重也采用同样的方式进行分解。

4.基于mvvae模型的图像处理

当mvvae模型收敛之后，可以得到优化的编码器参数和解码器参数然后将测试集的图像输入到模型中，通过该网络，可以重构出相应的图像y。

本发明主要用于图像重构、图像去噪和图像补全。

当用于图像重构时，使用变分下界来衡量重构误差，如公式(10)所示。特别地，变分下界的值越大，则说明重构的样本图像越接近原图像。

当用于图像去噪和补全时，先对测试图像加入噪声或者部分遮挡，然后输入到训练好的mvvae模型中，通过该网络，可以重构出相应的干净图像。使用峰值信噪比(psnr)、归一化均方误差(nmse)和结构相似性(ssim)对重构效果进行客观评价。

本发明在公开的数据集上进行实验，并通过与向量变量自编码器(vae)的对比，来验证本发明在图像重构、图像去噪和图像补全问题上的优越性。实验主要分为两大部分，第一个是进行图像重构实验，旨在验证mvvae模型能够很好的重构图像。第二个主要是进行图像去除噪声和对缺失图像的补全实验，旨在验证mvvae能更好地建模观测变量的统计分布信息，并且样本点的各维度之间存在相关性，当部分维度缺失时，可以通过相关信息得到填补。

本发明所用实验数据集如下：

mnistdatabase：该数据库包括10个数字类别(0～9)的60000个训练样本和10000个测试样本，每个样本由28×28的像素组成，将每个像素的值归一化为[0,1]之间。

yaledatabase：该数据库是在不同的光照和表情下获取的人脸图像，包括15个人，每个人11幅图像(共165幅)。本发明中随机选取每个人的8幅图像作为训练样本(共120幅)，剩余的图像作为测试样本，将每个样本下采样到64×64，并且进行了灰度化处理，然后再将图像的灰度值标准化到[0,1]之间。

实验1：在mnist数据集mvvae模型的图像重构效果评价

首先，进行图像的重构对比实验。探讨在mvvae模型和vae模型中不同潜在变量维度大小和不同隐藏层变量维度大小下对mnist重构误差的影响。因为该实验涉及两个变量维度的改变，所以采用控制变量法的原理，先固定隐藏层变量的维度大小为20×20，然后改变潜在变量维度的大小，在训练过程中mvvae模型和vae模型使用相同的神经网络结构，重构效果如图2所示。

从图中可以看出，潜在变量维度大小在10×10以内，通过不断的增大潜在矩阵变量维度的大小，则变分下界不断变大，说明重构效果较好。但是如果潜在变量维度大小增大到15×15，则重构效果反而会下降，这可能跟隐层节点维度有关，当隐层节点维度固定时，无限制的增大潜在变量节点维度，模型的重构性能不一定更优。通过mvvae模型(实线)和vae模型(虚线)重构效果的对比，则mvvae重构的效果更好。

下面，固定潜在变量维度的大小为10×10，然后改变隐藏层变量维度的大小，重构效果如图3所示。从图中可以看出，当不断地增大隐藏层变量的维度大小时，变分下界逐渐升高，当隐层变量维度增大至30×30时，与隐藏层变量维度为20×20变分下界的值持平，即达到相近的重构的效果。因此在mnist数据集的实验中，选择隐层节点维度大小为20×20，潜在层节点维度大小为10×10。

从图中可以看出，mvvae模型比vae模型展示出了更好的重构效果，这是因为mvvae模型的输入层、隐藏层和潜在变量层均为矩阵变量形式，更好的保留了2d矩阵数据的内部空间结构。

实验2：基于mvvae的图像去噪和缺失图像补全效果评价

为了验证mvvae模型可以从数据中学习到概率统计分布信息，进行了图像去除噪声和对缺失数据进行填补实验。首先进行去除噪声实验，从mnist训练集中选出5000张数字为9的样本进行训练，设置隐藏层矩阵变量的大小为20×20，潜在层矩阵变量的大小为10×10，学习率为0.0001，梯度下降率为0.00001，批处理的块大小为100，迭代次数均为10次。在测试集中选择1000张数字为9的样本随机加入10％的椒盐噪声，然后分别使用mvvae模型和vae模型进行去噪。原始测试图像如图4(a)所示，增加噪声的测试图像如图4(b)所示，其对应的用vae模型去除噪声图像如图4(c)所示,用mvvae模型去除噪声图像如图4(d)所示。

可以看出，vae模型重建结果比较模糊，而mvvae模型重建结果更清晰。同时使用峰值信噪比(psnr)和归一化均方误差(nmse)对vae模型和mvvae模型重构效果进行客观评价，如表1所示。可以看出mvvae模型的psnr较高并且nmse较低，说明使用mvvae模型重构的图像失真较小，更接近原图像。

表1vae模型和mvvae模型对mnist图像进行去噪的客观评价

其次，对缺失数据的进行补全实验。这一实验主要是在yale和ar数据库上进行测试，对比的方法为mvvae算法和vae算法。首先使用yale人脸的训练图像分别训练两个模型，然后在测试图像上加入随机噪声遮挡块，遮挡块的大小为20×20。因为样本点的各维度之间存在相关性，所以当部分维度缺失时，可以通过相关信息得到填补，两个模型的重构效果如图5所示。

可以看出，使用vae模型补全的人脸图像噪声点比较多，重构出的图像也比较暗。而使用mvvae模型重构的图像比较清晰，并且亮度高，更真实。同时使用峰值信噪比(psnr)、归一化均方误差(nmse)和结构相似性(ssim)对vae模型和mvvae模型重构效果进行客观评价，ssim主要从亮度、对比度和结构三个方面度量图像的相似性，值越高说明重构的图像失真越小。如表2所示，可以看出mvvae模型重构的效果更优。

表2vae模型和mvvae模型对人脸图像补全的客观评价