一种基于子空间投影和字典学习的图像分类方法与流程

本发明涉及到模式识别中的领域自适应图像分类领域，尤其涉及一种基于子空间投影和字典学习的域自适应图像分类领域。
背景技术：
：在传统的模式识别和机器学习中，算法需要在一定的假设条件下才能有良好的表现，最常见的是：源域的训练集样本和目标域的测试集样本在分布上要保持一致。而在实际应用中，往往很难满足这个条件。例如：在图像分类领域，图像传感器的不同种类，拍摄角度的不同，不同的光线条件等，都会使训练集和测试集样本之间存在较大的分布差异。分布差异会导致训练好的分类器在实际处理测试集样本时表现不佳，大多数方法需要重新训练分类器，而训练分类器需要充足的带标签样本，在某些应用场景下，收集带标签的样本需要付出昂贵的代价甚至无法完成，领域自适应方法就致力于解决这个问题。解决领域自适应问题的其中一种方法是基于特征的自适应，在图像分类领域，一幅图像会通过各种各样的特征提取方法将其从像素矩阵转换为特征向量，面对图像分布不同带来的差异，这类方法从特征向量着手，通过子空间投影，特征变换等方式来减小图像分布差异给分类带来的影响。较有代表性的是杨蒙(音)教授提出的fddl字典学习方法和boqinggong等人提出的gfk方法。fddl方法使用线性判别条件，对每一类的样本构造一个子字典，并通过整个字典将样本线性表示出来。gfk方法基于核方法，将数据嵌入到grassmann流形中，取得了不错的效果。最近效果比较好的方法是s.herath等人提出的额ils方法，即学习一个不变的潜在子空间，将训练集样本和测试集样本投影到该子空间上，从而减小了分布的差异。技术实现要素：本发明所要解决的技术问题针对
背景技术：
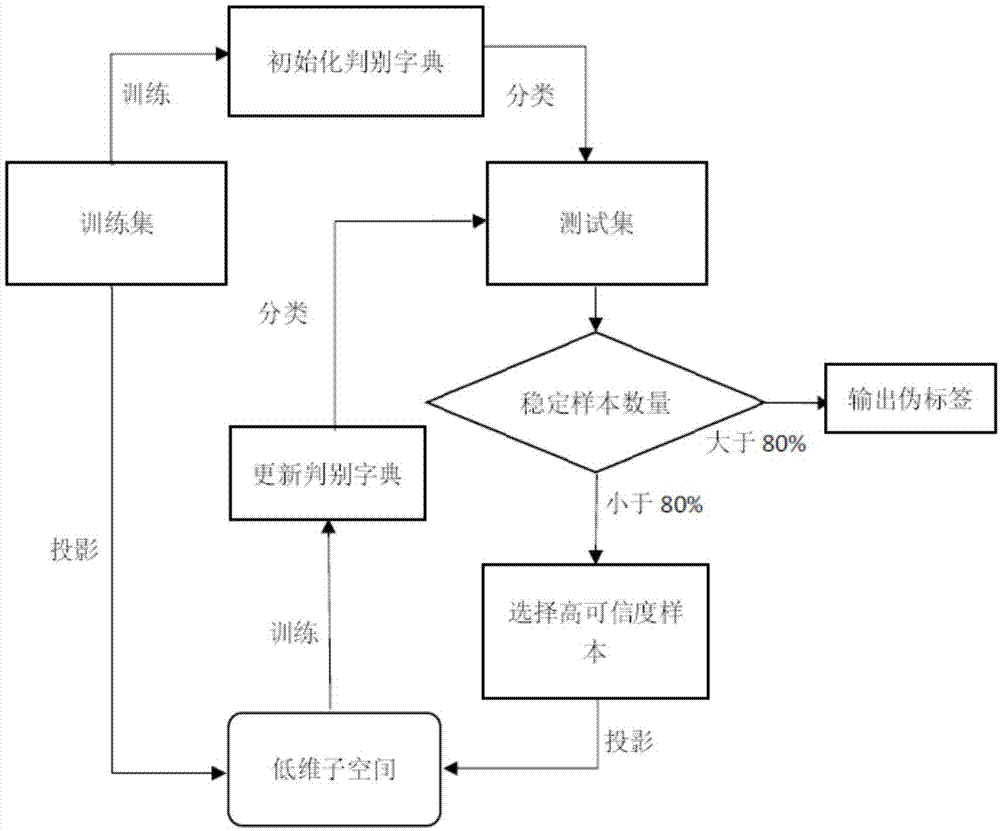
中所涉及到的缺陷，提供一种基于子空间投影和字典学习的图像分类方法，解决了在不重新训练分类器的条件下，源域的训练集和目标域的测试集样本分布过大带来的分类器表现不佳的问题。为了达到以上目的，本发明提出了一种基于子空间投影和字典学习的图像分类方法,包括以下步骤：步骤1)使用带标签的训练集初始化判别字典并给测试集样本加上伪标签；步骤2)选出具有高可信度的测试集样本；步骤3)将高可信度的测试集样本和训练集样本分别投影到低维平面上，在低维平面上学习判别字典，同时联合学习投影矩阵；步骤4)使用学习到的判别字典再次对测试集样本进行分类，即重新加上伪标签；步骤5)计算稳定样本个数，若其数量大于等于测试集样本数量的80％则结束迭代过程，输出该轮伪标签作为结果；若小于80％则重复步骤2～5直到满足条件。进一步的，所述步骤1)的详细步骤如下：假设给定的训练集中包含c类样本，即标签l＝{1,…,c},是训练集样本，是测试集样本，ns，nt分别是训练集和测试集样本的数量，n1，n2分别是训练集和测试集样本的特征维数；用表示第k轮的判别字典，表示第j类的子字典，其中n为低维子空间的维数，k是整个字典的原子数，x＝[x1，…,xn]∈rk×n是n个样本由判别字典d的稀疏表示；‖·‖f指矩阵的frobenius范数，即指矩阵各元素平方和开平方；‖·‖2是矩阵的2范数，即指该矩阵的协方差矩阵最大特征值开平方；步骤1.1)用带标签的训练集样本，通过线性判别字典学习的方法来初始化判别字典d(0)，即通过最小化下式来使字典能够很好的使用原子线性表达出样本，并且能够通过稀疏表示系数x来对样本进行分类：其中对第i个样本xin和xo1t分别为步骤1.2)学习到字典d(1)后，给测试集样本加上伪标签,给第i个测试集样本加伪标签的方法如式(2)：其中是使用第j类子字典重建第i个测试集样本的稀疏系数。进一步的，所述步骤2)的详细步骤如下：由步骤1.2)给第i个测试集样本加上伪标签之后，通过计算每个训练集样本的置信度来衡量伪标签的可信度；在第k轮迭代过程中，第i个样本被分类到第j类的置信度由式(3)定义：即对第i个测试集样本，现得到长度为c的向量其值除了伪标签所属的项外都为零，即若共有c＝5类，第i个样本伪标签为2，则其中为使用第k轮学习到的字典中的第j类子字典重建第i个测试集样本的重建误差，即在第k轮迭代学习到更新后的字典后，分别使用第j个子字典来重建第i个测试集样本，由式(4)给出：其中是将测试集样本投影到低维子空间的投影矩阵；为了得到伪标签可信度最大的q％*nt个测试集样本，以置信度为依据选择矩阵挑出所有类样本中可信度最大的前q％个样本，w的每一个元素，即为零一变量，指出第i个样本在挑选第j类时是否被选中，若被选中则为1，否则为0，其中q是一个固定常数，根据训练集大小而定，一般取50％；挑选第j类样本的方法如式(5)：s.t.||wj(k)||0＝q％*nt,j＝1,…,c(5)其中是第j类样本的选择矩阵，它是一个对角矩阵，其对角线上的元素为选择矩阵第j列的元素；同样地，也是对角矩阵，其对角线上的元素是置信度矩阵c(k)的第j列；||wj(k)||0是wj(k)矩阵中非零元素的个数，即确保每一类中只有q％被选出；至此得到每一类的选择矩阵wj(k)，通过式(6)将选出的每一类高可信度样本加入字典的训练过程中，即更新用于下一轮训练的测试集样本：进一步的，所述步骤3)的详细步骤如下：步骤3.1)假设投影矩阵和n为投影后子空间的维数，则投影到低维子空间上后的训练集样本为测试集样本为在这个低维平面上利用式(7)训练集样本和挑选之后的测试集样本学习字典，并联合学习投影矩阵ps和pt且||xj||0≤t0,t0为稀疏系数其中即将两个投影矩阵邻接在一起，同理其次，即将ys和yt作为块矩阵的对角，其余的块矩阵为零，trace指矩阵的迹，即矩阵主对角线上元素之和；f1使用利用pspt将分别将训练集样本和测试集样本投影到低维子空间中，并在低维子空间中联合学习判别字典d和‖·‖0指矩阵或向量的零范数，即向量中非零元素的个数，‖·‖f指矩阵的frobenius范数，即指矩阵各元素平方和开平方；f2是训练集样本和测试集样本的最大均值距离(mmd)，衡量了训练集样本和测试集样本在分布上的差异，分布差异越小，f2的取值越接近0；其中矩阵由式(8)给出：f3是将样本反投影的过程，期望在投影过程中损失尽可能少的样本信息；步骤3.2)在求解式(7)的优化问题时引入矩阵和b，分别满足:ps＝(ysas)t(9)pt＝(ytat)t(10)式(7)的优化方程可转换为：且||xj||1≤t0,t0为稀疏系数经过整理式(12)可得到：需要求的变量有三个，在这里本发明采取固定其他先求其中一个的策略，即先固定求再迭代固定求当被固定时，它们可被看作常数，固式中只剩下为未知量；首先将初始化，方法是：先将k进行特征值分解得到：k＝vsvt(14)其中，v是特征向量矩阵，s是一个对角矩阵，其对角线上的元素是矩阵k的特征值，本方法将as及at的列向量初始化为前n大的特征值所对应的特征向量，即对特征值从大到小排列之后，选取最大的前n个特征值对应的特征向量构成或这里的n是将为后平面的维数；在得到的初始值后，式中还有未知量和由于未知量可转换为d和我们利用多次迭代的方法求解，求解d和的具体步骤如下：将d初始化为随机的单位向量，则式中只剩下为未知量，先将初始化为全o向量再采取逐列更新的方式来计算为第i类样本系数表示的稀疏系数；在第h轮中，更新的公式为：其中，是第h轮更新得到的稀疏系数是函数q(x)对的偏导数，其中，q(x)由下式给出：由式(15)解得后，固定式中的同样利用逐列更新的方法来求解d，即每次更新字典d中的一列dj,更新dj的公式为：其中，z是经过投影的样本即至此，求得了d(k)和利用下式求出则固定和求解由式(13)(14)可令：可将式(13)转换为如下的形式:{g}＝argmingtrace(gthg)(17)其中g＝[gs,gt],式(16)需要利用stiefel流形来求解，可直接调用现成的软件包，求得g；至此得到更新的公式为：可由式(9)和(10)分别解出ps和pt，至此，已由式(16)求得d(k)，由式(9)和(10)分别解出ps和pt。进一步的，所述步骤4)的详细步骤如下：在得到本轮求得的字典d(k)以及投影矩阵后，用下式更新第i个测试集样本的伪标签：进一步的，所述步骤5)的详细步骤如下：将所有的测试集样本的伪标签都更新完后，将其与该样本上一轮的伪标签进行比较，若两轮得到的伪标签相同，则称该样本为稳定样本，计算稳定样本的数量；若该数量大于测试集样本总数的q％,则样本和字典都趋于稳定，结束迭代并将最后一轮测试集样本的伪标签输出，作为最后的结果；若稳定样本数量小于测试集样本总数的q％，则继续迭代直到不满足条件为止。本发明采用以上技术方案与现有技术相比，具有以下技术效果：1.能够通过联合学习子空间和字典的方法，显著的减小训练集和测试集样本之间的分布差异。2.能够挖掘测试集样本中潜在的判别信息来加入训练分类器过程，即伪标签，并使其具有较高的可信度。3.能够处理训练集样本和测试集样本异构的情况，即当训练集样本转化的特征向量与测试集样本转化的特征向量具有不同的维数时，多数算法无法处理，而本发明具有较好的应对方法。附图说明图1是本发明基于子空间投影和字典学习的图像分类的工作流程图。具体实施方式针对迁移学习中的领域自适应问题(源域为少量带标签的训练集图像，目标域为充足的不带标签的测试集图像，训练集和测试集图像之间存在较大的分布差异),我们的目标是通过算法，使得在训练集上训练的分类器能够在目标域的测试集样本上有良好的分类效果。下面结合附图对本发明的技术方案做进一步的详细说明：本发明公开了一种基于子空间投影和字典学习的图像分类方法：在使用训练集样本初始化字典后，使用字典给测试集样本加上伪标签，并挑选出伪标签具有高可信度的测试集样本加入迭代训练字典的过程。将带有标签的训练集样本和带有伪标签的测试集样本通过两个投影矩阵分别投影到低维子空间上，并在子空间上联合学习判别字典与投影矩阵，使用学习到的判别字典对所有的测试集样本进行重分类得到各自新的伪标签，则完成一轮迭代，每次迭代得到新的判别字典，新的投影矩阵和新的测试集样本伪标签。本发明将新伪标签与上轮伪标签相同的测试集样本称为稳定样本，每轮迭代结束后计算稳定样本的数量，如果稳定样本的数量小于测试集样本总数的百分之八十，则继续迭代过程，如果在一轮迭代之后稳定样本的数量占测试集样本总数的百分之八十及以上，则迭代结束，输出本轮得到的测试集样本伪标签作为最后的分类结果。本发明所述的基于子空间投影和字典学习的图像分类方法，包括以下步骤：(一)初始化判别字典并使用字典给测试集样本加上伪标签假设给定的训练集中包含c类样本即标签l＝{1,…,c},是训练集样本，是测试集样本。ns，nt分别是训练集和测试集样本的数量。n1，n2分别是训练集和测试集样本的特征维数。用表示第k轮的判别字典，表示第j类的子字典，其中n为低维子空间的维数，k是整个字典的原子数。最后，x＝[x1，…,xn]∈rk×n是n个样本由判别字典d的稀疏表示。‖·‖f指矩阵的frobenius范数，即指矩阵各元素平方和开平方。‖·‖2是矩阵的2范数，即指该矩阵的协方差矩阵最大特征值开平方。步骤1.1)用带标签的训练集样本，通过线性判别字典学习的方法来初始化判别字典d(0)，即通过最小化下式来使字典能够很好的使用原子线性表达出样本，并且能够通过稀疏表示系数x来对样本进行分类：其中对第i个样本xin和x0ut分别为可逐列对d进行更新得到d(1)步骤1.2)学习到字典d(1)后，给测试集样本加上伪标签,给第i个测试集样本加伪标签的方法如式(2)：其中是使用第j类子字典重建第i个测试集样本的稀疏系数。将所有的测试集样本加上标签之后得到即为第一轮的伪标签。(二)选出高可信度的测试集样本给第i个测试集样本加上伪标签之后，本发明通过计算每个训练集样本的置信度来衡量伪标签的可信度。在第k轮迭代过程中，第i个样本被分类到第j类的置信度由式(3)定义：即对第i个测试集样本，现得到长度为c的向量其值除了伪标签所属的项外都为零，即若共有c＝5类，第i个样本伪标签为2，则其中为使用第k轮学习到的字典中的第j类子字典重建第i个测试集样本的重建误差，即在第k轮迭代学习到更新后的字典后，分别使用其所有的子字典来重建第i个测试集样本。由式(4)给出：其中是将测试集样本投影到低维子空间的投影矩阵为了得到伪标签可信度最大的q％*nt个测试集样本，本发明以置信度为依据选择矩阵挑出所有类样本中可信度最大的前q％个样本，w的每一个元素，即为零一变量，指出第i个样本在挑选第j类时是否被选中。若被选中则为1，否则为0，其中q是一个固定常数，根据训练集大小而定，一般取50％。挑选第j类样本的方法如式(5)：其中是第j类样本的选择矩阵，它是一个对角矩阵，其对角线上的元素为选择矩阵第j列的元素。同样地，也是对角矩阵，其对角线上的元素是置信度矩阵c(k)的第j列。||wj(k)||0是wj(k)矩阵中非零元素的个数，即确保每一类中只有q％被选出。至此得到每一类的选择矩阵wj(k)，通过式(6)将选出的每一类高可信度样本加入字典的训练过程中，即更新用于下一轮训练的测试集样本：yj(k+1)＝[ytwj(k)]，j＝1,…,c(6)(三)投影并联合学习投影矩阵和字典假设投影矩阵和n为投影后子空间的维数，则投影到低维子空间上后的训练集样本为测试集样本为在这个低维平面上利用式(7)训练集样本和挑选之后的测试集样本学习字典，并联合学习投影矩阵ps和pt且||xj||0≤t0,t0为稀疏系数其中即将两个投影矩阵邻接在一起，同理其次，即将ys和yt作为块矩阵的对角，其余的块矩阵为零。trace指矩阵的迹，即矩阵主对角线上元素之和。f1使用利用pspt将分别将训练集样本和测试集样本投影到低维子空间中，并在低维子空间中联合学习判别字典d和指矩阵或向量的零范数，即向量中非零元素的个数，‖·‖f指矩阵的frobenius范数，即指矩阵各元素平方和开平方。f2是训练集样本和测试集样本的最大均值距离(mmd)，衡量了训练集样本和测试集样本在分布上的差异，分布差异越小，f2的取值越接近0。其中矩阵由式(8)给出：f3是将样本反投影的过程，期望在投影过程中损失尽可能少的样本信息在求解式(7)的优化问题时引入矩阵和b，分别满足:ps＝(ysas)t(9)pt＝(ytat)t(10)于是式(7)的优化方程可转换为：且||xj||1≤t0,t0为稀疏系数经过整理式(12)可得到：其中m为之前提到过的mmd矩阵。需要求的变量有三个，在这里本发明采取固定其他先求其中一个的策略，即先固定求再迭代固定求当被固定时，它们可被看作常数，式中只剩下为未知量。首先我们将初始化，方法是：将k进行特征值分解得到：k＝vsvt(14)其中，v是特征向量矩阵，s是一个对角矩阵，其对角线上的元素是矩阵k的特征值，本方法将as及at的列向量初始化为前n大的特征值所对应的特征向量，即对特征值从大到小排列之后，选取最大的前n个特征值对应的特征向量构成或这里的n是将为后平面的维数。在得到的初始值后，式中还有未知量和由于未知量可转换为d和我们利用多次迭代的方法求解，求解d和的具体步骤如下：我们将d初始化为随机的单位向量，则式中只剩下为未知量，我们先将初始化为全o向量再采取逐列更新的方式来计算为第i类样本系数表示的稀疏系数。在第h轮中，更新的公式为：其中，是第h轮更新得到的稀疏系数，是函数q(x)对的偏导数，式中q(x)由下式给出由式(15)解得后，固定式中的同样利用逐列更新的方法来求解d，即每次更新字典d中的一列dj,更新dj的公式为：其中，z是经过投影的样本即至此，我们已经将求得了d(k)和可利用下式求出则我们可以固定和求解由式(13)(14)可令：可将式(13)转换为如下的形式:{g}＝argmingtrace(gthg)(17)其中g＝[gs,gt],式(16)需要利用stiefel流形来求解，可直接调用现成的软件包,求得g。至此得到更新的公式为：可由式(9)和(10)分别解出ps和pt。至此，我们已由式(16)求得d(k)，由式(9)和(10)分别解出ps和pt。(四)更新测试集样本的伪标签得到本轮求得的字典d(k)以及投影矩阵后，用下式更新第i个测试集样本的伪标签：(五)判定稳定样本的数量将所有的测试集样本的伪标签都更新完后，将其与该样本上一轮的伪标签进行比较，若两轮得到的伪标签相同，则称该样本为稳定样本，计算稳定样本的数量。若该数量大于测试集样本总数的q％,则样本和字典都趋于稳定，结束迭代并将最后一轮测试集样本的伪标签输出，作为最后的结果。若稳定样本数量小于测试集样本总数的q％，则继续迭代直到不满足条件为止。将本发明所述的基于子空间投影和字典学习的图像分类方法在office和caltech-256数据库上进行实验，并将实验结果与其他相关的域自适应方法进行对比分析。office数据库包含三个域的图片，即有三组样本可作为训练集或测试集，分别为amazon，webcam，dslr。amazon(以下称a)数据集是从网络商店上下载来的一些图片，dslr(以下称d)数据集是用slr相机拍出的高分辨率照片，webcam(以下称w)数据集是网络相机拍出来的低分辨率照片，caltech-256(以下称c)数据集是加州理工大学收集的一些办公物品的照片。每张图片都提取它的surf特征并使用k-means聚类，将其转换为一个800维的向量。我们把四个数据集分别当作源域的训练集和目标域的测试集，即可有种排列，我们选取了其中的一部分作为实验，实验的平均分类正确率如下：表一：各方法在office和caltech-256数据库上的分类结果a→ww→dw→aw→cd→ac→ac→dfddl31.260.330.622.832.138.138.2gfk35.771.235.529.336.240.441.1ils40.672.438.632.638.948.644.4本发明41.877.242.833.839.148.350.2领域从表一中可以看出，本发明所提出的方法相对于其他方法，有较高的分类正确率。本
技术领域：
技术人员可以理解的是，除非另外定义，这里使用的所有术语(包括技术术语和科学术语)具有与本发明所属领域中的普通技术人员的一般理解相同的意义。还应该理解的是，诸如通用字典中定义的那些术语应该被理解为具有与现有技术的上下文中的意义一致的意义，并且除非像这里一样定义，不会用理想化或过于正式的含义来解释。以上所述的具体实施方式，对本发明的目的、技术方案和有益效果进行了进一步详细说明，所应理解的是，以上所述仅为本发明的具体实施方式而已，并不用于限制本发明，凡在本发明的精神和原则之内，所做的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。当前第1页12