人群疏散宏观模型迭代式仿真方法与流程

本发明涉及人群疏散仿真领域，尤其是涉及一种人群疏散宏观模型迭代式仿真方法。

背景技术

近年来，随着社会经济的高速发展，公共场所内经常会出现大规模人群聚集现象。通常来说在人群较为密集的场所中，疏散一直是棘手的问题，安全隐患也日益突出，在拥塞环境中出现的拥挤踩踏等突发事件造成了生命财产的重大损失。因此如何规避人群密集场景下的拥塞事件，减少生命财产的损失，一直是安全领域研究的热点问题。随着科学技术的发展，人群运动仿真技术成为研究的热点。通过仿真手段模拟研究人群疏散的行为规律，其费用开销小等优势对在紧急情况发生时人群的疏散具有重大的现实意义。

仿真方法是建立系统的数学模型并将它转换为适合在计算机上编程的仿真模型，然后对模型进行仿真试验的方法。对人群疏散的仿真，根据仿真时所采用的模型的不同，可分为模拟仿真法、数字仿真法和混合仿真法三类。人群疏散的微观模型适用于模拟仿真方法，宏观模型适用于数字仿真方法，而微宏观混合的模型适用于混合仿真方法。

到目前为止，对于人群疏散仿真方法的研究，尚存在现有的仿真方法存在仿真结果与真实情况相差较大、仿真结果真实性差等若干不足。

技术实现要素：

本发明的目的就是为了克服上述现有技术存在的缺陷而提供一种人群疏散宏观模型迭代式仿真方法。

本发明的目的可以通过以下技术方案来实现：

一种人群疏散宏观模型迭代式仿真方法，包括以下步骤：

1)建立aw-rascle人群动力学宏观模型；

2)基于地形环境进行行人高斯分布初始化；

3)基于初始化的所述行人流高斯分布和aw-rascle人群动力学宏观模型进行迭代式仿真，并显示仿真结果。

进一步地，进行丁字路口仿真时，在步骤1)中，在所述aw-rascle人群动力学宏观模型中引入交叉口区域的影响矩阵。

进一步地，所述步骤2)包括：

201)设置丁字路口的地形环境，对丁字路口的主干道和支干道进行网格化；

202)以高斯分布初始化各网格的人群密度。

进一步地，所述人群密度ρ(x，y)的表达式为：

式中，ρ(x，y)为坐标(x，y)处的人群密度，dmax为最大的人群密度值，a和b分别为垂直和水平方向密度分布的中心横纵坐标。

进一步地，所述迭代式仿真中，各网格的人群密度受周围邻近的所有网格中人群的排斥力、目的地对所在网格人群的吸引力以及人群的恐慌状态的作用而发生变化。

进一步地，所述迭代式仿真具体为：

301)从网格化的坐标原点开始，按时间步长依次进行相邻网格的人群密度变化，所有网格的人群密度均发生改变后，完成一次迭代；

302)以上一次迭代得到的各网格的人群密度为下一次迭代的初始值，重复执行步骤301)，直至达到最大仿真迭代次数。

与现有技术相比，本发明具有以下有益效果：

1、将迭代的思想与仿真过程结合起来，促使仿真结果更加接近真实情景。

现有的人群疏散仿真方法没有运用迭代的思想，其仿真的效果往往不能很好地反映现实的人群疏散的状况。而迭代式的仿真方法，采用多次迭代仿真的思路，随着仿真次数的增加，能够使仿真的结果最大限度地接近实际人群疏散的状况。迭代式的仿真方法能够使仿真的效果更加接近真实情况，并且随着迭代次数的增加，仿真的效果越好。

2、仿真结果的可视化与人群分布态势判断

现有的技术侧重于对人群疏散的理论性研究，从理论上分析人群疏散过程中的趋势变化，清晰明确的仿真结果展示较少。本发明利用所提出的人群疏散宏观模型迭代式仿真方法，运用matlabr2017a编写程序，对丁字路口进行建模仿真。通过仿真得到的人群密度等高线图和热力分布图，能够迅速识别区域的人群密度以及人群分布的态势，进而对人群疏散的状态有更加清晰直观的了解。所以仿真结果的可视化与人群分布态势判断是本项发明的又一优点。

附图说明

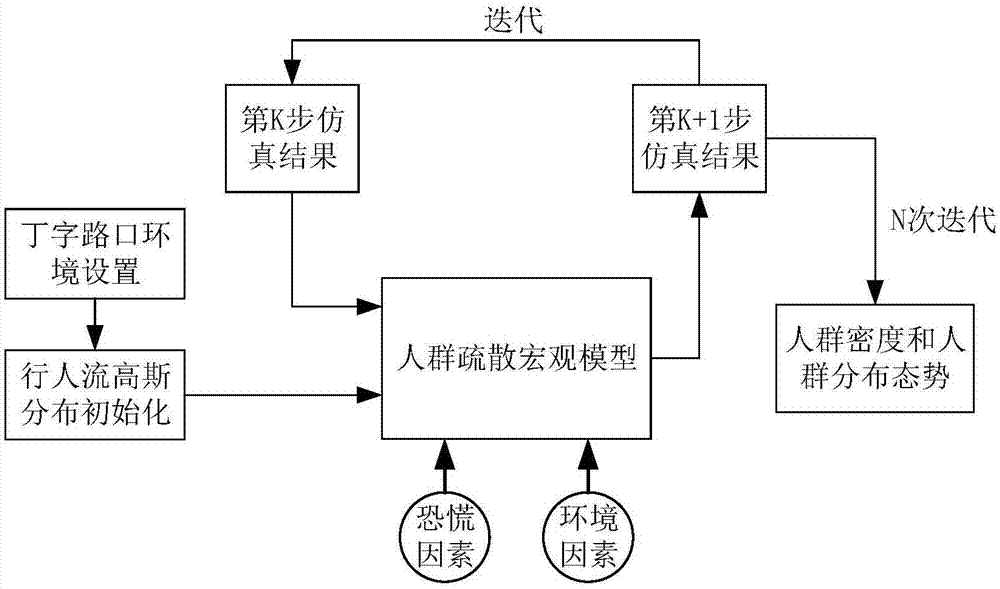
图1为本发明的流程示意图；

图2为丁字路口示意图；

图3为本发明区域网格化示意图；

图4为2015年麦加朝圣的踩踏事件的位置；

图5为迭代次数n＝5的丁字路口人群密度等高线图；

图6为迭代次数n＝20的丁字路口人群密度等高线图；

图7为迭代次数n＝80的丁字路口人群密度等高线图；

图8为迭代次数n＝5的丁字路口人群热力学图；

图9为迭代次数n＝20的丁字路口人群热力学图；

图10为迭代次数n＝80的丁字路口人群热力学图。

具体实施方式

下面结合附图和具体实施例对本发明进行详细说明。本实施例以本发明技术方案为前提进行实施，给出了详细的实施方式和具体的操作过程，但本发明的保护范围不限于下述的实施例。

如图1所示，本发明提供一种人群疏散宏观模型迭代式仿真方法，包括以下步骤：1)建立aw-rascle人群动力学宏观模型；2)基于地形环境进行行人高斯分布初始化；3)基于初始化的所述行人流高斯分布和aw-rascle人群动力学宏观模型进行迭代式仿真，并显示仿真结果。迭代式的仿真方法能够使仿真的效果更加接近真实情况。

1、建立aw-rascle人群动力学宏观模型

a.aw和m.rascle基于一维流量模型提出了二维空间的人群疏散模型(简称aw-rascle模型)。aw-rascle模型是由两个非线性双曲线偏微分方程(partialdifferentialequations，pde)所构成的模型。其中，方程式(1)由质量守恒的偏微分方程来决定，ρ和v表示行人密度和速度，ρt是时间的偏导数，(ρv)x是距离x的偏导数。

ρt+(ρv)x＝0(1)

在高阶模型中，假设ρ和v是独立的，方程式(2)用二维的偏微分方程来反映ρ和v的关系。其中p(ρ)表示该模型中的“压力”项，v表示水平速度，u表示垂直速度。

(v+p(ρ)t)+v(v+p(ρ))x＝0(2)

将该模型的第一个偏微分方程由一维系统转成二维系统。

ρt+(ρv)x+(ρu)y＝0(3)

为了用流体运动的各向异性来反映疏散人群的各向异性，定义“压力”项。用流量φ对时间的导数来反映信息传播的趋势，考虑用流量的对流导数(全导数)作为预期因素，如式(4)。

由此，得到使速度处于平衡状态的松弛项s1和s２。

其中τ是松弛时间，速度v(ρ)是水平方向的最大速度，u(ρ)是垂直方向的最大速度。

(v+ph)t+v(v+ph)x+u(u+ph)y＝s1(7)

(v+pv)t+v(v+pv)x+u(u+pv)y＝s2(8)

二维aw-rascle人群动力学模型由公式(3)、(7)、(8)组成，ph是水平方向的压力项，pv是垂直方向的压力项。初始条件为ρ(x，y，0)≥0，v(x，0)≤|vf1|和u(y，0)≤|vf2|，vf1和vf2是两个方向疏散个体的最大速度。其中ph(ρ，v)和pv(ρ，v)函数由式(9)和式(10)给出。

其中，β、γ均为常数。

在aw-rascle人群疏散模型的基础上，丁字路口人群疏散动力学模型增加了在丁字路口区域矢量在垂直方向u和矢量水平方向v双向叠加的影响，使得交叉口位置处的行人密度分布更加合理。引入交叉口区域的影响矩阵mimp，解决双向叠加问题。

其中，c是最大影响系数，i和j是疏散个体在交叉口区域的横坐标和纵坐标，vij为坐标为(i，j)处的水平速度，uij为坐标为(i，j)处的垂直速度，矩阵中的元素为交叉口区域坐标为(i，j)处的影响因子，由对水平方向速度偏导后的影响因子和对垂直方向速度偏导后的影响因了经向量合成获得。

2、环境设置和行人高斯分布初始化

行人流高斯分布初始化包括：设置丁字路口的地形环境，对丁字路口的主干道和支干道进行网格化；以高斯分布初始化各网格的人群密度。

(1)丁字路口地形环境设置

在aw-rascle人群动力学宏观模型的基础上，将迭代式仿真方法应用于丁字路口的人群疏散情况。丁字路口是容易发生踩踏事故的地段，所以研究丁字路口的人群疏散仿真方法具有很大的现实意义。丁字路口的平面简化图如图2所示。

为了更好地描述仿真的过程，需要将丁字路口的主干道和支干道网格化，如图3所示。而网格的个数则根据实际的情况和计算机的仿真能力来设定。

(2)行人流高斯分布初始化

传统的人群疏散动力学模型使用由二维空间给出的高斯分布，如式(12)所示。

ρ(x，y)为坐标(x，y)处的人群密度，dmax为最大的人群密度值，a和b分别为垂直和水平方向密度分布的中心横纵坐标。密度值指的是每单位面积的行人数，为了实现模拟实例的目的，可以设定最大密度值dmax为7.0p/m²(人/每平米)。水平和垂直方向的行人速度为vf1和vf2，根据相关研究假定vf1＝vf2＝1.36ms^-1。

本发明使用改进后的高斯分布，如式(13)所示，将高斯函数调整为较高阶平滑函数，在交点处引入纵横比1/a*b作为高斯分布的因子，并将σ值作为松弛量，以求更加接近实际人群的总体分布状态。

3、迭代式仿真

所述迭代式仿真中，各网格的人群密度受周围邻近的所有网格中人群的排斥力、目的地对所在网格人群的吸引力以及人群的恐慌状态的作用而发生变化。迭代式仿真具体为：

301)从网格化的坐标原点开始，按时间步长依次进行相邻网格的人群密度变化，所有网格的人群密度均发生改变后，完成一次迭代；

302)以上一次迭代得到的各网格的人群密度为下一次迭代的初始值，重复执行步骤301)，直至达到最大仿真迭代次数。

迭代是重复反馈过程的活动，其目的通常是为了逼近所需目标或结果。每一次对过程的重复称为一次“迭代”，而每一次迭代得到的结果会作为下一次迭代的初始值。

(1)初次迭代

根据高斯分布初始化公式，每一个网格中均有初始人群密度ρ(x，y)，它受周围邻近的所有网格中人群的排斥力、目的地对人群的吸引力以及人群的恐慌状态的作用而发生变化。而仿真从坐标的原点开始，处于坐标(1，1)位置的网格人群密度ρ(1，1)首先开始变化，一个时间步长后变成下个时间步长后，ρ(1，2)和ρ(2，1)相应地变化成和不断执行仿真，直到所有网格的人群密度ρ(x，y)均发生改变，则完成初次迭代。

(2)n次迭代

将初次迭代得到各个网格的人群密度作为下次迭代的初始值，继续新一轮的仿真。一轮仿真结束之后，判断仿真次数是否达到的设定的仿真次数n，如果没有达到，则继续进行迭代，直到仿真次数达到n次。最终得到仿真之后的区域人群密度而迭代次数越多，仿真的结果则更加接近真实的情况。迭代式仿真的仿真路线图如图1所示。

实施例

本实施例中，用丁字路口人群疏散动力学模型对2015年麦加踩踏的事件进行研究，通过仿真重现发生在204街和223街(204-223交界处)之间的t形路口的踩踏事件，踩踏事件的位置如图4所示。2015年06时(格林尼治标准时间09时09分)，该踩踏事件发生在204街和223街的t形路口处。最初人群主要分布在204街道，并依次向前移动，进行朝觐。223街道上的大巴车下载一批乘客，当这部分人群进入到223和204街道的交叉口处，两个方向的人群发生对冲，碰撞导致人群摔倒发生踩踏，然而背后的人群，不了解前方的挤塞情况，不断前进，导致了朝圣者之间的大面积的踩踏事件。

根据204街和223街交叉口踩踏事件的实际参数，在街道上设置2000名疏散人员作为初始条件。基于本专利提出的仿真方法，编写matlab程序，计算并得到可视化仿真结果——丁字路口人群疏散密度等高线图，如图5、6、7所示。通过密度等高线图，可以得到每个区域的人群密度。同时，仿真也可以得到丁字路口人群疏散热力学图，如图8、9、10所示。该图表明了人群的分布态势，而且由于迭代次数的增加，可以发现仿真的效果更加接近真实的状况。

以上详细描述了本发明的较佳具体实施例。应当理解，本领域的普通技术人员无需创造性劳动就可以根据本发明的构思作出诸多修改和变化。因此，凡本技术领域中技术人员依本发明的构思在现有技术的基础上通过逻辑分析、推理或者有限的实验可以得到的技术方案，皆应在由权利要求书所确定的保护范围内。