对象和属性同时增加的矩阵动态属性约简方法与流程

本发明涉及数据挖掘中粗糙集及粒计算理论技术领域，特别是涉及对象和属性同时增加的矩阵动态属性约简方法。

背景技术

目前随着计算机网络、存储及通信技术的快速发展，各行各业都积累了各种海量应用数据，而且这些应用数据在现实中不断地动态变化，用传统属性约简算法去计算这些动态数据，需要重复计算，导致运行时间消耗巨大，这使得传统数据挖掘方法不能及时、有效地解决动态数据中知识发现的问题。增量学习技术能够模拟人的认知机理，可以充分利用原有的运行结果对新增加进来的知识进行动态更新和修正，从而使更新后的知识更具有实时性，极大地降低动态数据分析处理对时间和空间的需求，提高了数据挖掘的效率。这在一定程度上更能满足社会实际的需求。

由于传统属性约简算法主要是利用数学中集合的交与并运算操作来实现，计算及表示形式都比较抽象和复杂。矩阵是非常实用的数学计算工具，它因表示形式直观、计算操作简单等优势，已经被广泛应用到工程计算和科学研究等领域，用矩阵的方法处理动态数据集属性约简的问题具有非常重要理论价值和实践价值。

技术实现要素：

本发明实施例提供了对象和属性同时增加的矩阵动态属性约简方法，可以解决现有技术中存在的问题。

本发明提供了对象和属性同时增加的矩阵动态属性约简方法，该方法包括以下步骤：

步骤1，输入变化前的决策表、增量对象集、增量属性集、变化前决策表的相对知识粒度、条件属性等价关系矩阵、变化前决策表的最小属性约简及最小属性约简的相对知识粒度；

步骤2，当增量对象集添加到决策表后，计算增加增量对象后决策表的等价关系增量矩阵以及增量对象等价关系矩阵；

步骤3，当增量属性集添加到决策表后，计算增量属性等价关系矩阵以及增加增量属性后决策表的等价关系增量矩阵；

步骤4，当增量对象集添加到决策表后，根据步骤2得到的增加增量对象后决策表的等价关系增量矩阵和增量对象等价关系矩阵计算变化后决策表的等价关系矩阵；

步骤5，当增量对象集和增量属性集添加到决策表后，利用步骤2和步骤3得到的增加增量对象后决策表的等价关系增量矩阵、增加增量属性后决策表的等价关系增量矩阵和增量对象等价关系矩阵计算变化后决策表的等价关系矩阵；

步骤6，根据变化前决策表的相对知识粒度计算增量对象集的相对知识粒度，在变化前决策表的相对知识粒度和增量对象集的相对知识粒度的基础上，通过基于矩阵方法的增量机制计算变化后决策表的相对知识粒度，在最小属性约简的相对知识粒度和最小属性约简增量对象集的相对知识粒度的基础上计算最小属性约简在变化后决策表的相对知识粒度，如果变化后决策表的相对知识粒度与最小属性约简在变化后决策表的相对知识粒度相等，则跳转执行步骤9，否则跳转执行步骤7；

步骤7，计算决策表增加增量对象集和增量属性集后每个属性a相对于变化前决策表最小属性约简的外部重要性，循环选取最大的外部重要性a0并将其添加到决策表最小属性约简中，计算增加属性a0后最小属性约简的相对知识粒度，直到其与变化后决策表的相对知识粒度相等为止；

步骤8，对于最小属性约简中的每个属性a，计算最小属性约简删掉属性a后的相对知识粒度，如果最小属性约简删掉属性a后的相对知识粒度与变化后决策表的相对知识粒度相等，则将属性a从最小属性约简中删除，最后得到的属性约简为变化后决策表的最小属性约简；

步骤9，输出变化后决策表的最小属性约简。

本发明实施例中的对象和属性同时增加的矩阵动态属性约简方法，当一些对象和属性同时添加到决策表后，在变化前决策表的等价关系矩阵和相对知识粒度基础上，通过基于矩阵方法的增量机制，计算变化后决策表的等价关系增量矩阵及相对知识粒度。在变化前决策表最小属性约简的基础上，设计了基于矩阵方法的动态属性约简算法，能够有效地解决决策表中对象集和属性集动态增加时如何快速计算最小约简的问题。当一些新属性和新对象同时添加到决策表后，求解变化后决策表的最小约简，基于矩阵方法的非动态属性约简算法计算变化后决策表的最小约简时，需要重新开始计算，导致计算最小约简的时间消耗巨大；而采用本发明的基于矩阵方法的动态属性约简算法能够通过变化前决策表的等价关系、相对知识粒度以及最小约简的基础上，利用增量机制计算变化后决策表的等价关系矩阵和相对知识粒度，能够快速获得变化后决策表的最小约简。因此，本发明算法求解变化后决策表最小约简的计算时间小于基于矩阵方法的非动态属性约简算法的计算时间。

与现有属性约简技术相比较，本发明的积极效果如下：

一、区别于传统属性约简算法，本发明通过矩阵方法计算决策表的等价关系矩阵、相对知识粒度及属性的内部和外部重要性等知识，表示形式直观，计算操作简单，容易实现。

由于传统属性约简算法主要是利用数学中集合的交与并运算操作来实现，计算及表示形式都比较抽象和复杂。本发明提出的基于矩阵方法的动态属性约简算法中的很多数值都是通过矩阵运算而获得，由于现实生活中很多软件工具(如matlab等)都能有效地处理矩阵运算的问题，故本发明提出的基于矩阵方法的动态属性约简算法可以借助上述软件工具来实现。

二、区别于传统属性约简算法，当决策表增加对象和属性后，本发明通过使用增量机制能够快速找到变化后决策表的最小约简。

目前现有的大多数属性约简算法均为静态数据集设计的，在处理动态数据集约简时，因不能有效利用原有的运行结果，使得传统数据挖掘方法不能及时、有效地解决动态数据中知识发现的问题。由于现实中很多决策表中的对象和属性都是动态增加的，本发明通过基于矩阵方法的增量机制，在变化前决策表的等价关系矩阵、相对知识粒度及最小属性约简的基础上，能够快速获得变化后决策表的等价关系矩阵、相对知识粒度及最小属性约简，极大地降低动态数据分析处理对时间和空间的需求，提高了动态数据挖掘和知识发现的效率，从而使更新后的知识更具有实时性。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

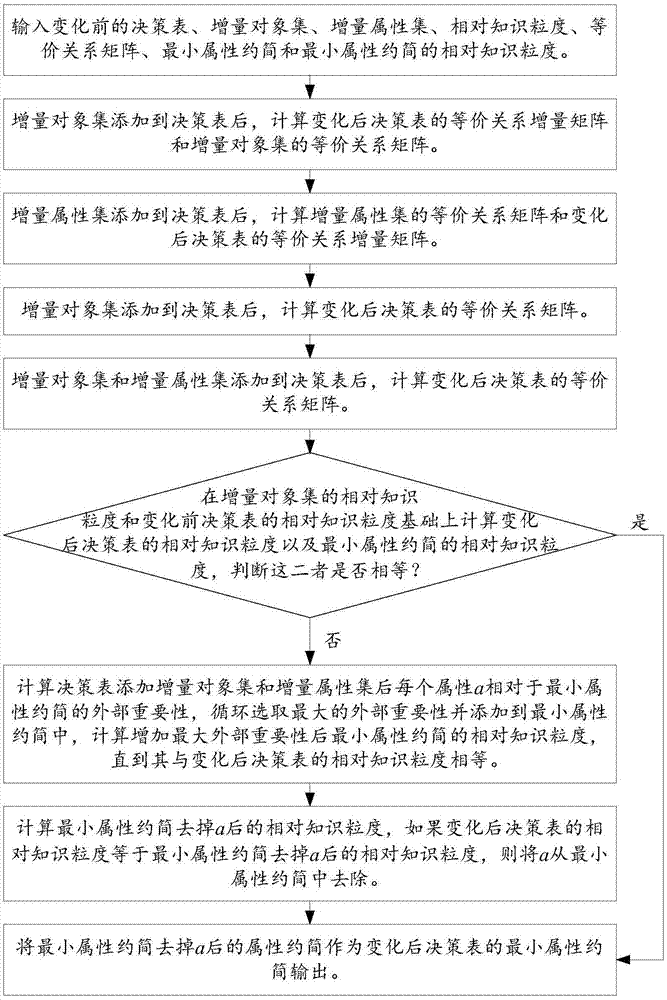
图1为本发明实施例提供的对象和属性同时增加的矩阵动态属性约简方法的流程图；

图2为本发明针对6个不同数据集，利用基于矩阵方法的动态属性约简算法与非动态属性约简算法计算决策表最小约简运行时间比较结果图；

图3为本发明针对同时增加不同大小属性集和对象集时，利用基于矩阵方法的动态属性约简算法与非动态属性约简算法计算决策表最小约简运行时间比较结果图。

具体实施方式

下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

参照图1，本发明实施例提供了对象和属性同时增加的矩阵动态属性约简方法，该方法包括以下步骤：

步骤1，输入变化前的决策表、增量对象集ux、增量属性集p、变化前决策表的相对知识粒度gpu(d|c)、条件属性等价关系矩阵变化前决策表的最小属性约简redu及redu的相对知识粒度gpu(d|redu)。其中变化前的决策表包括对象集u、条件属性集c、决策属性集d以及对象的属性值。

步骤2，当增量对象集ux添加到决策表后，计算增加增量对象后决策表的等价关系增量矩阵根据变化前的决策表的条件属性等价关系矩阵计算增量对象等价关系矩阵其中rc表示在条件属性集c下决策表的等价关系。

步骤3，当增量属性集p添加到决策表后，根据变化前的决策表的条件属性等价关系矩阵计算增量属性等价关系矩阵根据和计算增加增量属性后决策表的等价关系增量矩阵

步骤4，当增量对象集ux添加到决策表后，根据步骤2得到的增加增量对象后决策表的等价关系增量矩阵和增量对象等价关系矩阵计算变化后决策表的等价关系矩阵其中rc∪p表示在条件属性集c和增量属性集p下决策表的等价关系。

步骤5，当增量对象集ux和增量属性集p添加到决策表后，利用步骤2和步骤3得到的增加增量对象后决策表的等价关系增量矩阵、增加增量属性后决策表的等价关系增量矩阵和增量对象等价关系矩阵计算变化后决策表的等价关系矩阵

步骤6，根据变化前决策表的相对知识粒度计算增量对象集ux的相对知识粒度在相对知识粒度gpu(d|c)和的基础上，通过基于矩阵方法的增量机制计算变化后决策表的相对知识粒度其中为变化后决策表的等价关系矩阵，为变化前决策表的条件属性等价关系矩阵，是决策表增加增量属性后的等价关系增量矩阵，为决策表增加增量对象后的等价关系增量矩阵，为决策表增加增量对象和增量属性后的等价关系增量矩阵，是分别是的转置矩阵，为增量对象等价关系矩阵，是决策表增加条件属性和决策属性后的等价关系矩阵，是增量对象集的条件属性和决策属性的等价关系增量矩阵，为变化后决策表的条件属性和决策属性的等价关系增量矩阵，是变化后决策表增加增量对象后条件属性的等价关系增量矩阵，是变化后决策表增加增量对象后条件属性和决策属性的等价关系增量矩阵，为变化后决策表的相对知识粒度，gpu(d|c)为变化前决策表的相对知识粒度，为增量对象集的相对知识粒度，|u∪ux|是变化后决策表中所有对象的个数，|u|是变化前决策表中所有对象的个数，|ux|是增量对象集中所有对象的个数，sum(·)t×n为矩阵所有元素的和，|·|²代表对象个数的平方，其中rc∪d表示在条件属性集c和决策属性集d下决策表的等价关系。在相对知识粒度gpu(d|redu)和的基础上计算最小属性约简redu在变化后决策表的相对知识粒度如果则跳转执行步骤9，否则跳转执行步骤7。其中，为条件属性等价关系矩阵的算术平均值，为条件属性和决策属性等价关系矩阵的算术平均值。

步骤7，根据公式计算决策表增加增量对象集和增量属性集后每个属性a相对于最小属性约简redu的外部重要性依次循环选取最大的外部重要性并将其添加到最小属性约简redu中，即redu←redu∪{a0}，计算增加属性a0后redu的相对知识粒度，直到其与变化后决策表的相对知识粒度相等为止。

步骤8，对于最小属性约简redu中的每个属性a，计算redu删掉属性a后的相对知识粒度如果则将属性a从redu中删除，即redu←redu-{a}，最后得到的最小属性约简redu为变化后决策表的最小属性约简。

步骤9，将redu赋值给输出变化后决策表的最小约简

本发明中对象和属性同时增加的矩阵动态属性约简方法，在变化前决策表的条件属性等价关系矩阵变化前决策表的相对知识粒度gpu(d|c)、最小属性约简redu及最小约简的相对知识粒度gpu(d|redu)的基础上，当增量对象集ux和增量属性集p添加到决策表后，通过矩阵增量机制计算变化后决策表的相对知识粒度及redu在变化后决策表的相对知识粒度并判断他们是否相等，如果则redu是变化后决策表的最小属性约简。如果利用矩阵方法和增量机制计算变化后决策表除redu之外其他所有属性的外部重要性，依次选取外部重要性最大的属性并添加到最小属性约简redu中，并计算添加属性后redu的相对知识粒度并与变化后决策表的相对知识粒度相比较，直到它与变化后决策表的相对知识粒度相等为止；最后依次删除redu中的冗余属性，获得变化后决策表的最小属性约简

为了验证本发明所提出的基于矩阵方法动态属性约简算法的有效性，在uci机器学习公用数据集网站中下载了dermatology、cancer、kr-vs-kp、mushroom、ticdata2000、letter6个数据集作为本发明的仿真实验验证的数据，并把计算最小属性约简的运行时间和约简的数值作为本发明的评估指标。

仿真实验一

为了说明本发明所提出的基于矩阵方法动态属性约简算法的有效性，把dermatology、cancer、kr-vs-kp、mushroom、ticdata2000、letter中的每个数据集的50％对象集、50％的条件属性集及决策属性集作为基本数据集，把剩余的对象集和属性集分别作为增量对象数据集和增量属性集，当把增量对象集和增量属性集动态添加到基本数据集，得到变化后决策表进行仿真试验，并与非动态属性约简算法进行了对比分析，仿真实验结果表明：两种算法所获得变化后决策表的最小约简的数值是相近的，其中某些数据集中的最小约简数值是完全相同的，但基于矩阵方法动态属性约简算法能够快速获得变化后决策表的最小约简。基于矩阵方法的动态属性约简算法与非动态属性约简算法计算变化后决策表最小约简的运行时间比较结果如图2所示，图中的x轴为不同数据集，y轴为不同算法属性约简的运行时间的常用对数值(由于约简运行时间差异较大，为了使图形能够客观地反映不同算法的趋势，所以y轴为不同算法属性约简运行时间的常用对数值表示)，在同一个数据集的两个的柱状图中，左侧为非动态属性约简得到的结果，右侧为本发明动态属性约简得到的结果。从图2容易得到，与非动态属性约简算法相比，本发明所提出的算法计算变化后决策表最小约简的运行时间较少，特别是针对较大数据集letter时，本发明所提出的算法计算最小约简运行时间的优势更加明显。

仿真实验二

随着决策表的对象和属性的不断增加，基于矩阵方法动态属性约简算法是否有效？为了进一步验证本发明是有效的，给出了依次增加不同百分比的对象和属性进行仿真实验验证。本发明把dermatology、cancer、kr-vs-kp、mushroom、ticdata2000、letter中的每个数据集的50％对象集、50％的条件属性集及决策属性集作为基本数据集，把剩余的对象集和属性集分别选择20％、40％、60％、80％、100％的数据作为增量对象数据集和属性集逐次添加到基本数据集后，得到变化后决策表进行仿真试验。相关的仿真试验结果如图3所示，图中的x轴为增加的大小不同的属性集和对象集，y轴为不同算法属性约简的运行时间的常用对数值(由于约简运行时间差异较大，为了使图形能够客观地反映不同算法的趋势，所以y轴为不同算法属性约简运行时间的常用对数值表示)，(a)为把不同百分比的属性和对象同时增加到dermatology数据集时，利用基于矩阵方法的动态属性约简算法与非动态属性约简算法计算决策表最小约简运行时间比较结果图，(b)为把不同百分比的属性和对象同时增加到cancer数据集时，利用基于矩阵方法的动态属性约简算法与非动态属性约简算法计算决策表最小约简运行时间比较结果图，(c)为把不同百分比的属性和对象同时增加到kr-vs-kp数据集时，利用基于矩阵方法的动态属性约简算法与非动态属性约简算法计算决策表最小约简运行时间比较结果图，(d)为把不同百分比的属性和对象同时增加到mushroom数据集时，利用基于矩阵方法的动态属性约简算法与非动态属性约简算法计算决策表最小约简运行时间比较结果图，(e)为把不同百分比的属性和对象同时增加到ticdata2000数据集时，利用基于矩阵方法的动态属性约简算法与非动态属性约简算法计算决策表最小约简运行时间比较结果图，(f)为把不同百分比的属性和对象同时增加到letter数据集时，利用基于矩阵方法的动态属性约简算法与非动态属性约简算法计算决策表最小约简运行时间比较结果图。从图3容易得到，随着数据集的增加，本发明算法求解变化后决策表最小约简的计算时间小于非动态属性约简算法的计算时间，这在某种程度上说明了本发明提出的算法在处理动态数据集的最小约简是合理的。

尽管已描述了本发明的优选实施例，但本领域内的技术人员一旦得知了基本创造性概念，则可对这些实施例作出另外的变更和修改。所以，所附权利要求意欲解释为包括优选实施例以及落入本发明范围的所有变更和修改。

显然，本领域的技术人员可以对本发明进行各种改动和变型而不脱离本发明的精神和范围。这样，倘若本发明的这些修改和变型属于本发明权利要求及其等同技术的范围之内，则本发明也意图包含这些改动和变型在内。