利用一条直线及帕斯卡定理标定拋物折反射摄像机的方法与流程

本发明属于计算机视觉领域，涉及一种利用空间中一条直线及帕斯卡定理求解抛物折反射摄像机内参数的方法。

背景技术

计算机视觉的中心任务就是对图像进行理解，而它的最终目标是使计算机具有通过二维图像认知三维环境信息的能力。这种能力将不仅使机器能感知包括形状、姿态、运动等在内的三维环境中物体的几何信息，而且能对它们进行描述、存储、识别与理解。摄像机标定就是确定从三维空间点到它的二维图像点之间的映射关系，它是许多计算机视觉应用必不可少的步骤。为了确定这一映射过程，需要建立摄像机的几何成像模型，几何模型的参数称为摄像机参数，摄像机参数可分为内参数和外参数两类。内参数描述成像系统的成像几何特性，外参数描述成像系统关于世界坐标系的方向和位置。摄像机标定可分为传统标定、自标定和基于几何实体的标定。无论哪种标定方法，都旨在建立二维图像与摄像机内参数之间的约束关系，特别是线性约束关系，这是目前摄像机标定所追求的目标，也是目前计算机视觉领域研究的热点之一。

抛物折反射摄像机由一个抛物镜面和一个正交摄像机组成，它的成像视野大，是全景视觉领域研究的热点之一。文献“catadioptricself-calibration”，(kangs.b.,proceedingsofieeeconferenceoncomputervisionandpatternrecognition,vol.1,pp.201-207,2000)提出了一种折反射摄像机自标定方法，这类方法的优点是不需要使用标定块，缺点是必须获得图像之间的对应点。而在计算机视觉中，实现一个十分有效的寻找对应点的方法是很困难的。文献“geometricpropertiesofcentralcatadioptriclineimagesandtheirapplicationincalibration”,(barretoj.p.,araujoh.,ieeetransactionsonpatternanalysisandmachineintelligence,vol.27,no.8,pp.1327-1333,2005)研究了中心折反射摄像机下直线的像的几何性质，并将这些性质应用于中心折反射摄像机的标定。文献“usingconcurrentlinesincentralcatadioptriccameracalibration”,(leizhang,xindu,ji-linliu,journalofzhejianguniversitysciencec,vol.41,vol.12,issue3,pp239–249,2011)介绍了利用共点线和直线的性质提出了一个由繁化简的标定方法，将非线性最小化标定问题分成几个线性子问题，从而可获得中心折反射摄像机内参数。文献“calibrationofcentralcatadioptriccamerasusingadlt-likeapproach”,(puigl.,bastanlary.,sturmp.,etal.internationaljournalofcomputervision,vol.93,no.1,pp.101-114,2011)提出了一种基于三维控制点的标定方法，通过使用veronese映射对三维点和其图像点的坐标进行了扩展，在扩展坐标的基础上基于dlt(直接线性变换)——相似方法实现了中心折反射摄像机的标定，但是这类方法需要已知三维点的位置，并且容易从图像中提取其图像点。

直线在空间中是很常见的，无需知道标定的直线和摄像机的位置关系，只利用线像标定摄像机。文献“catadioptriccameracalibrationusinggeometricinvariants”，(yingx.,huz.,ieeetransactionsonpatternanalysisandmachineintelligence,vol.26,no.10,pp.1260-1271,2004)首次提出了利用球或者直线标定中心折反射摄像机。在非退化情况下一条直线的投影二次曲线提供三个不变量。但是该文献提出的标定方法是非线性的，计算的复杂度较高。文献“geometricpropertiesofcentralcatadioptriclineimagesandtheirapplicationincalibration”，(barretoj.,araujoh.,ieeetransactionsonpatternanalysisandmachineintelligence,vol.27,no.8,pp.1327-1333,2005)研究了直线在中心折反射摄像机下的几何性质，根据射影不变性应用这些性质标定摄像机内参数，三条及其以上的直线就可完成摄像机内参数的标定。文献“identicalprojectivegeometricpropertiesofcentralcatadioptriclineimagesandsphereimageswithapplicationstocalibration”，(yingx.,zhah.,internationaljournalofcomputervision,vol.78,no.1,pp.89-105,2008)介绍了修正绝对二次曲线的像(miac)在中心折反射摄像机标定中的作用。他们通过研究球或直线在中心折反射摄像机下的像与miac的几何与代数关系提出了两种线性标定算法。它们得出的结论对于对偶形式也是成立的。但是这篇文献中的理论和标定方法对于抛物折反射摄像机的情况是退化的。

技术实现要素：

本发明提供了一种制作简单，适用广泛，稳定性好的利用靶标求解抛物折反射摄像机内参数的方法，该靶标由空间中一条直线构成。在求解抛物折反射摄像机内参数的过程中，需使用抛物折反射摄像机拍摄靶标的3幅图像求解出抛物折反射摄像机的5个内参数。

本发明采用如下技术方案：

用抛物折反射摄像机从不同的位置拍摄3幅含有一条直线的图像。本发明是利用空间中一条直线作为靶标用于求解抛物折反射摄像机内参数的方法。首先，分别从3幅图像中提取靶标图像边缘点，使用最小二乘法拟合获得靶标方程。在线像上取三个点，根据帕斯卡定理及其推论获得关于圆环点的像的非线性方程，同时圆环点的像也位于线像上，从而联立方程获得关于圆环点的像的非线性方程组。利用牛顿迭代法求解方程组从而获得圆环点的像，三幅图像提供三组圆环点的像。最后，利用圆环点的像对绝对二次曲线像的约束求解摄像机内参数。具体的步骤包括：拟合出靶标投影方程，得到关于圆环点的像的方程组，确定圆环点的像，求解抛物折反射摄像机内参数。

1.拟合靶标投影方程

利用matlab程序中的edge函数提取靶标图像边缘点的像素坐标，并用最小二乘法拟合获得线像的方程。

2.关于圆环点的像的获取

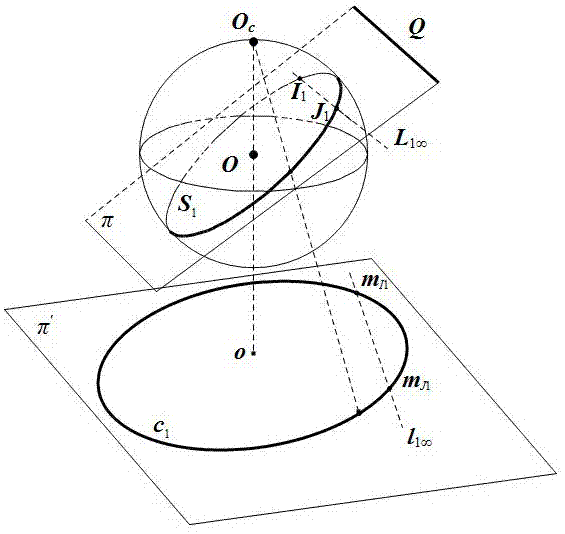
空间中的直线q，在拋物折反射摄像机的单位球模型下的投影分为两步。第一步，以单位视球的球心o为中心，直线q的投影是单位视球上的投影大圆sn(n＝1,2,3表示拍摄的三幅图像)，简称大圆。第二步，以单位视球表面上的一点oc为投影中心，这里oc可看作一个摄像机的光心，将大圆sn投影为抛物折反射图像平面上的二次曲线cn。抛物折反射图像平面与光轴oco垂直。令以oc为光心的摄像机的内参数矩阵为其中rc是纵横比，fc是有效焦距，s是倾斜因子，[u0v01]^t是摄像机主点o的齐次坐标矩阵形式，其中rc,fc,s,u0,v0为折反射摄像机的5个内参数。利用matlab中的edge函数提取3幅图像靶标图像边缘点的像素坐标，通过最小二乘法拟合得到相应的二次曲线方程。这里用cn分别表示第n(n＝1,2,3)幅图像中的线像的系数矩阵。本文为了简化表述，用相同字母表示曲线和它的系数矩阵。

根据圆环点的定义，大圆s1与该平面π上的无穷远直线l1∞的交点是圆环点i1,j1也是投影大圆s1上的点；对于任意一个内接于非退化的二阶曲线的简单六点形，它的三对对边的交点在一条直线上，这条直线称为帕斯卡线；则取圆环点中的一个和其它五个点组成的简单六点形内接于投影圆s1也满足帕斯卡定理；将四点形看成六点形中有两对相邻顶点重合的情形，由投影大圆s1上任意三个点与圆环点的其中的一个组成的简单四点形，一对对边的交点与另一对对边中每一条与其对顶点的切线的交点，根据帕斯卡定理这三点共线；

在像平面π'上，用c1表示大圆s1的像，mi1,mj1分别表示i1,j1的像，而影消线l1∞是平面π上的无穷远直线l1∞的像。设c1上任取三个点为ma1,mb1,mc1，点ml1为ma1和mi1所成直线和与mb1和mc1所成直线的交点，点mm1为ma1和mb1所成直线与mc1的极线的交点，点mn1为mb1的极线与mc1和mi1所成直线的交点。因为ml1,mm1,mn1三点共线，所以有det(ml1,mm1,mn1)＝0，其中det(.)为行列式。又mi1在c1上，故有mi1^tc1mi1＝0。从而得到关于圆环点的像mi1,mj1的方程组。

3.确定圆环点的像

利用牛顿迭代法求解关于圆环点的像的非线性方程组，从而得到圆环点的像。

4.求解抛物折反射摄像机内参数

由圆环点的像mii,mji(i＝1,2,3)对绝对二次曲线的像ω的线性约束获得ω。即：其中re,im分别表示复数的实部和虚部。最后，根据对ω进行cholesky分解再求逆便得到内参数矩阵kc，即获得摄像机5个内参数。

本发明优点：

(1)该靶标制作简单，只需空间中任意一条直线。

(2)对该靶标的物理尺度没有要求，无需知道直线在世界坐标系中的位置。

附图说明

图1是用于求解抛物折反射摄像机内参数的靶标在单位视球上的示意图。

图2是靶标在抛物折反射图像平面上的投影。

具体实施方式

本发明提供了一种利用靶标求解抛物折反射摄像机内参数的方法，靶标是由空间中的一条直线构成，如图1。用此靶标完成抛物折反射摄像机内参数的求解需要经过以下步骤：从抛物折反射图像中提取靶标图像边缘点，使用最小二乘法拟合获得线像投影。利用本发明中的方法对实验的拋物折反射摄像机进行标定，从线像上任取三个点，根据帕斯卡定理及其推论得到两个关于圆环点的像的方程。又由圆环点的像位于线像上得到另外两个方程，联立方程组利用牛顿迭代法求解圆环点的像。获得3个不同方位的直线图像，得到三组圆环点的像。利用圆环点的像对绝对二次曲线像的约束求解摄像机内参数。具体步骤如下：

1.拟合靶标投影方程

利用matlab程序中的edge函数提取靶标图像边缘点的像素坐标，并用最小二乘法拟合获得线像的方程。

2.得到关于圆环点的像的方程组

空间中的直线q(如图1)，在拋物折反射摄像机的单位球模型下的投影分为两步。第一步，以单位视球球心为中心将直线q投影到单位视球上的大圆sn(n＝1,2,3)，如图1所示(n＝1为例)。第二步，通过摄像机的光心oc将大圆sn投影为抛物折反射图像平面上的二次曲线cn，如图1所示。利用matlab中的edge函数分别提取3幅图像中的靶标图像边缘点的像素坐标，通过最小二乘法拟合得到相应的二次曲线方程，这里cn表示第n(n＝1,2,3)幅图像中的线像的系数矩阵。

如图2所示，设圆环点的像mi1,mj1的齐次坐标分别为[a1+b1ie1+f1i1]^t，[a1-b1ie1-f1i1]^t，其中a1,b1,e1,f1为系数。设直线投影圆c1上任取三个点为ma1,mb1,mc1，点ml1为ma1和mi1所成直线和与mb1和mc1所成直线的交点，点mm1为ma1和mb1所成直线与mc1的极线的交点，点mn1为mb1的极线与mc1和mi1所成直线的交点。则有

(ma1×mi1)×(mb1×mc1)＝ml1，(1)

(ma1×mb1)×(c1·mc1)＝mm1，(2)

(c1·mb1)×(mc1×mi1)＝mn1。(3)

因为ml1,mm1,mn1三点共线，由(1)、(2)和(3)式有

det(ml1,mm1,mn1)＝0。(4)

又因圆环点的像mi1一定在二次曲线c1上，故有

mi1^tc1mi1＝0。(5)

又mi1是复点，则有

对于n＝2,3两幅线像c2,c3的关于圆环点的像的方程组可用类似的方法获得。

3.确定圆环点的像

方程组(6)是以a1,b1,e1,f1为未知数的非线性方程组，利用牛顿迭代法求解方程组(6)，解得a1,b1,e1,f1的值，从而得到圆环点的像。对于线像c2,c3上的圆环点的像mi2,mj2，mi3,mj3可用类似的方法获得。

4.求解抛物折反射摄像机内参数

由圆环点的像对绝对二次曲线的像的线性约束有：

可用最小二乘法优化求解(7)获得ω，最后对进行cholesky分解得再求逆便得到内参数矩阵kc，即获得摄像机5个内参数。

实施例

本发明提出了一种利用一条直线作为靶标线性确定抛物折反射摄像机内参数的方法。本发明采用的实验模板结构示意图如图1所示。下面以一实例对本发明的实施方案做出更为详细的描述。

基于空间中的抛物折反射摄像机标定采用的实验模板是空间中的一条直线，如图1所示，直线记为q。利用本发明中的方法对用于实验的抛物折反射摄像机进行标定，具体步骤如下：

1.拟合图像边界及靶标曲线方程

本发明采用的图像大小为1800×1700。用抛物折反射摄像机拍摄靶标的3幅实验图像，读入图像，利用matlab中的edge函数提取3幅图像靶标图像边缘点的像素坐标，并用最小二乘法拟合获得线像的方程。3幅线像的方程的系数矩阵分别为cn(n＝1,2,3)，结果如下：

2.圆环点像的获取

设圆环点像中的一个mi1＝[a1+b1ie1+f1i1]^t，任意在线像c1上取三个点分别为：

ma1＝[632.2535575994412747.30061457115171]^t，(11)

mb1＝[643.8912109243696744.800661273814541]^t，(12)

mc1＝[638.24347656381764.52197175139091]^t。(13)

对于线像c2,c3上也任取三个点分别为ma2,mb2,mc2和ma3,mb3,mc3，结果如下：

ma2＝[613.6230100480184665.28298744453081]^t，(14)

mb2＝[609.5777393651177701.44016990703341]^t，(15)

mc2＝[597.1566602224018688.37185785392001]^t；(16)

ma3＝[636.4231793237425715.42098851075361]^t，(17)

mb3＝[672.1727960994292788.83064845871461]^t，(18)

mc3＝[642.0287602310584767.61559132187151]^t。(19)

将(8)、(11)、(12)和(13)代入(1)、(2)和(3)可得ml1,mm1,mn1，其中*表示相乘，结果如下：

对于线像c2,c3上的ml2,mn2,mm2和ml3,mn3,mm3可用类似的方法得到，结果如下：

将(20)、(21)和(22)代入(4)，可获得关于a1,b1,e1,f1的方程，分离实部和虚部可获得两个方程。将(8)带入(5)分离实部和虚部也可获得两个方程。联立以上四个方程，利用牛顿迭代法求解该方程组可得圆环点的像，结果如下：

对于线像c2,c3上的圆环点的像mi2,mj2，mi3,mj3可用类似的方法获得，结果如下：

4.求解抛物折反射摄像机内参数

将(29)、(31)和(33)代入(7)得到ω中元素的线性方程组，使用svd分解求解该线性方程组得到ω的系数矩阵。结果如下：

最后，根据对(35)中的ω进行cholesky分解再求逆便可获得kc，结果如下：

其中纵横比rc＝kc(1，1)/kc(2,2)(kc(1,1)表示矩阵kc的第1行第1列的元素，kc(2,2)表示矩阵kc的第2行第2列的元素)，故抛物折反射摄像机的5个内参数分别为：rc＝1.090909079295，fc＝550.0000006911296，s＝0.3000002962677，u0＝449.9999998724358，v0＝349.9999999596385。