一种分布式水文模型的矩阵化模拟方法与流程

本发明属于分布式水文模型优化技术领域，具体涉及一种分布式水文模型的矩阵化模拟方法。

背景技术：

随着分布式水文模型的发展，越来越高的空间分布精度以及时间精度对水文模型的计算能力有了更大的要求；现有的逐点、逐时间段的方式已经不适用于高时空分辨率的分布式水文模型的计算。对于提升分布式水文模型计算能力的方法，现有的技术是通过并行计算的方式对已有的水文模型采取并行运算，以求最大化利用计算机处理器的计算能力。

譬如申请号为cn201310011570.6的中国专利公开了一种集群环境下分布式水文模拟的并行化方法，进行子流域划分和分级；以子流域为模版，将输入数据进行剖分并存入数据库；以子流域面积为计算量的衡量指标，同时考虑子流域间的拓扑关系进行计算任务划分；以子流域为单元，在集群环境下进行并行计算，其坡面过程计算采用静态调度，河道过程计算采用动态调度。又譬如申请号为cn201310066403.1的中国专利公开了一种全分布式流域生态水文模型的快速并行化方法，以栅格为基本计算单元，通过dem地形分析获得流域栅格流向图并建立栅格的计算依赖关系，将栅格单元垂向的生态水文过程模拟作为独立计算任务，根据栅格单元间的依赖关系解耦栅格单元计算任务并构建任务树，采用dag模型表达任务树，利用dag模型和边消除的动态调度算法动态地生成任务调度序列，并通过pbs动态调度器将栅格计算任务分配到不同的节点上进行运算，实现全分布式流域生态水文模型的并行化，极大的简化并行处理算法的并行逻辑控制，有效提高并行计算效率。然而，分布式水文模型涉及到诸多水文循环子过程的计算，其计算过程通常需要消耗很长的时间和很大的内存单元，譬如《分布式水文模型的并行计算》一文所总结的12个并行优化的结果，其最大的加速比为：82/100线程，优化使用了mpi并行运算技术和超多核硬件集群；并行计算的优化能力大大受限于计算集群的核心数目。

现有通过并行计算的方式对已有的水文模型采取并行运算的方法存在以下不可忽视的缺陷：一方面，最大优化比小于计算机(集群)的处理器数目，并行计算是将所有格点的计算量分配到不同的计算线程，对于单个的计算线程而言，仍然需要逐个计算所分配的格点过程；另一方面并行运算只是计算工具层面的解决办法，没有真正从分布式水文模型计算的原理出发，对计算效率的提升存在瓶颈。

技术实现要素：

针对现有技术的以上缺陷或改进需求，本发明提供了一种分布式水文模型的矩阵化模拟方法，其目的在于对整个分布式水文模型实现产汇流过程所有环节的矩阵化运算，克服现有并行处理方法的优化比受限于计算机或集群处理器数目的限制，提高模型运算速度。

为实现上述目的，按照本发明的一个方面，提供了一种分布式水文模型的多流程汇流过程矩阵化模拟方法，包括如下步骤：

(1)获取每个坡面格点的产流量，得到产流矩阵g，该产流矩阵的一个维度代表时间，另一个维度代表空间，即每个坡面格点的编号；

(2)根据河网与坡面的流向关系确定每个坡面格点对应的汇流点，本处汇流点即为河道格点，并将所有的坡面格点汇总得到多流程转移矩阵t；

(3)对产流矩阵和多流程转移矩阵进行矩阵的内积运算，得到汇流格点的汇流矩阵r；

r＝gt

其中：g的维度为pn×gn；t的维度为gn×rn；r的维度为pn×rn；pn是指时段数，gn是指坡面格点数，rn是指河道格点数目。

为实现本发明目的，按照本发明的另一个方面，提供了一种包括分段函数的分布式水文模型的矩阵化处理方法，包括如下步骤：

(1)对于分布式水文模型需要考虑的逐个子过程而言，如果不存在分段情况的处理，比如计算参考蒸散发，可以将所有格点的子过程通过一个矩阵实现并行计算；

(2)如果存在分段考虑的情况，比如计算土壤基流过程，将根据输入矩阵数据a判断土壤含水量对应的分段位置，确定分段数据对应的定义域[min,j]、(j,max]，并针对不同的分段建立分段定位转移矩阵b，令f(x)、g(x)分别为分段定位转移矩阵b定义域[min,j]、(j,max]上的计算公式；

(3)对需要分段考虑的土壤含水量输入矩阵数据a，将其和分段定位转移矩阵b进行矩阵的乘法运算，得到最终的格点基流输出数值r；从而，可以实现所有格点同时计算土壤基流过程，不用再依次判别逐个格点的土壤含水量去选择对应的计算函数。

总体而言，通过本发明所构思的以上技术方案与现有技术相比，能够取得下列有益效果：

(1)本发明提供的分布式水文模型的矩阵化模拟方法，在分布式水文模型的构建中采用矩阵化运算，将一些难以进行矩阵化运算的环节通过转移矩阵的形式进行优化，使得整个分布式水文模型基本实现产汇流过程所有环节的矩阵化运算，这种矩阵化运算通过化零为整，能够对进行同一运算的所有数据整理为一个集合，然后对集合进行整体运算；其优点在于，不需要判断某个数值的存储位置而直接运算，极大提高了模型计算效率，在很多支持向量运算的数学语言中，对矩阵运算的优化更为高效；解决了现有分布式水文模型的计算能力差、计算时间长的问题，打破了优化比受限于计算机(集群)处理器数目的限制，实现了分布式水文模型的高效运算。

(2)本发明提供的分布式水文模型的矩阵化模拟方法，对于分布式水文模型中的汇流过程模拟，不仅在空间维度上而且在时间维度上实现了矩阵化运算；在实际汇流过程中，每个坡面格点根据模拟的汇流路径汇流到不同的河道点；而现有技术的汇流过程模拟计算在采用单位线方法时，是将所有产流格点汇集到最终的一个出口格点；若将流域汇流过程的模拟改进为多流程汇流方式计算，仍采用逐个格点、逐时段进行计算的方法就会降低计算效率；而本发明提供的方法，通过提取每个格点的汇流属性并将其汇流特性转换为多流程转移矩阵，从而可以同时计算所有格点的汇流过程，因此克服了逐个格点、逐时段进行计算的方法的缺陷，提高了运算效率。

附图说明

图1是分段矩阵化处理的示意图；

图2是生成分段定位转移矩阵的流程示意图；

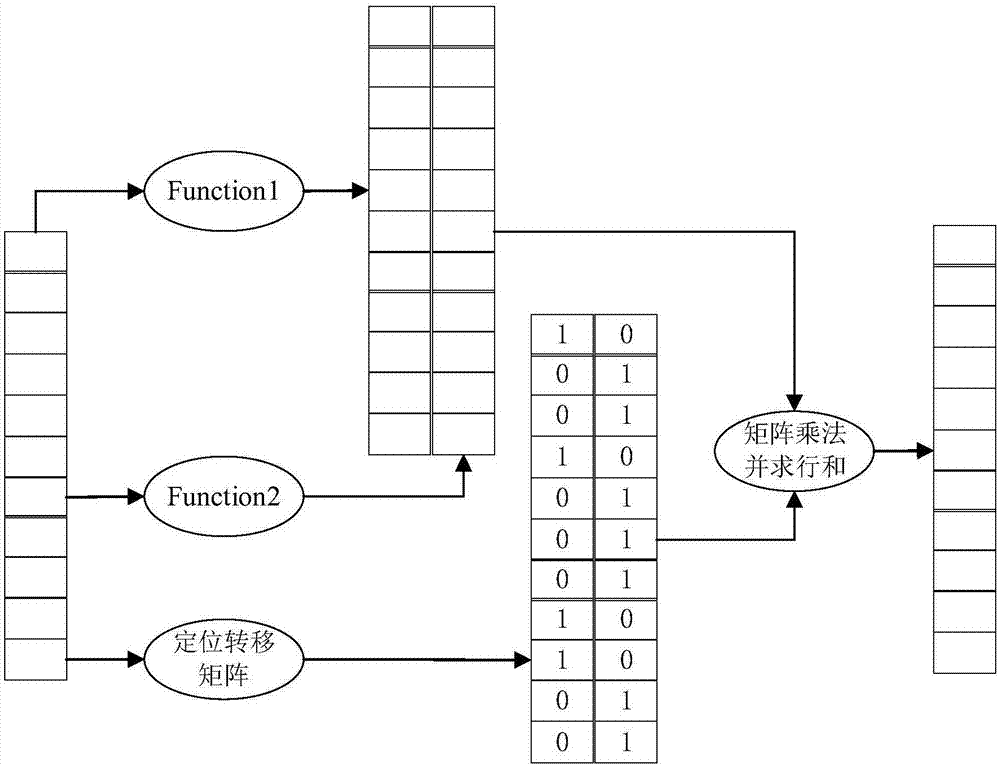
图3是多流程汇流矩阵化处理的示意图；

图4是生成多流程转移矩阵的流程示意图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。此外，下面所描述的本发明各个实施方式中所涉及到的技术特征只要彼此之间未构成冲突就可以相互组合。

参照图1，实施例提供的分布式水文模型的矩阵化模拟方法，对于采用分段函数表征土壤含水量的分布式水分模型而言，该方法包括如下步骤：

(1)根据输入矩阵数据a判断土壤含水量对应的分段位置，确定分段数据对应的定义域[min,j]、(j,max]，并针对不同的分段建立分段定位转移矩阵b；

(2)对需要分段处理的土壤含水量输入矩阵数据a，将其和分段定位转移矩阵b进行矩阵的乘法运算，得到最终的格点基流输出数值r，实现所有格点同时计算土壤基流过程。

以下是对长江寸滩水文站以上流域进行分布式水文模型的矩阵化模拟的实例；基流模块采用arno方法，基流计算模块中，根据土壤含水量不同使用到了分段函数：

式中：d为基流量；dmax为最大基流量；dmin为最小基流量；w为土壤含水量；wm为饱和土壤含水量；wd为一个土壤含水量的阈值。

采用本发明提供的矩阵化运算方法进行模拟，具体包括如下步骤：

(1)将土壤含水量在小于wd时和与等于wd时设定为两个分段的定义域，基流大小的计算公式则分别为这两个定义域上的计算函数；

(2)在确定格点土壤含水量的大小后，将根据格点土壤含水量所处的定义域选择相应的基流计算函数，形成分段定位转移矩阵；

当土壤含水量小于wd时，产生的基流量与饱和土壤含水量呈线性关系；当土壤含水量大于等于wd时，产生的基流量将呈非线性增长；

(3)在同时得到所有格点土壤含水量的基础上，将所有格点的土壤含水量输入矩阵数据和分段定位转移矩阵进行矩阵的乘法运算，得到最终所有格点的基流输出数值。

参照图2，生成分段定位转移矩阵的方法如下具体如下：

(2.1)格点编号i的初始值为1；

(2.2)确定待判断变量；

(2.3)判断待判断变量是否满足第i个条件；

(2.4)确定满足条件的变量对应的位置信息；将定位矩阵第i列对应位置赋值为1，令i＝i+1；

(2.5)判断i是否不大于分段总数，如果是，则进入到步骤(2.2)；否则，将得到的定位矩阵作为定位转移矩阵。

具体采用以下方法确定变量所在分段：

(a)将格点的土壤含水量与预设阈值wd相比，若小于wd，则将格点的土壤含水量属性定义为第一个分段定义域内的变量；

(b)若格点的土壤含水量大于等于wd，则将格点的土壤含水量属性定义为第二个分段定义域内的变量。

实测结果表明：在对311个计算单元(格点)1个时间段的基流计算中，其运算时间从0.3721309秒缩短至0.004218102秒，相比于逐个格点计算311个格点的基流过程，优化比高达88.2倍。

分布式水文模型涉及到诸多水文循环子过程的计算，在分布式水文模型中，有一个维度是代表最小计算单元的空间维度，另外一个维度则是时间序列。在空间维度上，如果每一个子过程在计算过程中，最小计算单元之间相互独立，则采用矩阵化运算的方法对所有参与该过程的最小计算单元同时进行处理以提高计算效率。矩阵化运算通过化零为整将进行同一运算的所有数据整理为一个集合，然后对集合进行整体运算；其优点在于不需要判断某个数值的存储位置而直接运算，而且在很多支持向量运算的数学语言中，对矩阵运算的优化更为高效。

在实际汇流过程中，每个坡面格点根据模拟的汇流路径汇流到不同的河道点，而当前的汇流过程计算在采用单位线方法时，一般是将所有产流格点汇集到最终的一个出口格点。若将流域汇流过程的模拟改进为多流程汇流方式计算时，仍采用逐个格点、逐时段的计算方法就会降低计算效率。为了提高多流程汇流方式的计算效率，实施例提出采用转移矩阵的矩阵化模拟方法，主要包括如下步骤：

(1)获取每个坡面格点的产流量，得到产流矩阵g，该产流矩阵的一个维度代表时间，另一个维度则为空间，即每个坡面格点的编号；

(2)根据河网与坡面的流向关系确定每个坡面格点对应的汇流点，本处汇流点即河道格点，并将所有的坡面格点汇总得到多流程转移矩阵t；

(3)对产流矩阵和多流程转移矩阵进行矩阵的内积运算，得到汇流格点的汇流矩阵r；

r＝gt

式中：g的维度为pn(时段数)×gn(坡面格点数)；t的维度为gn(坡面格点数)×rn(河道格点数目)；r的维度为pn(时段数)×rn(河道格点数目)。

参照图3，实施例中，研究范围内有g1～g8这8个坡面格点、r1与r2这2个河道格点，需要模拟从p1至p11这11个时段的汇流过程，包括如下步骤：

(1)获取每个坡面格点的产流量，得到产流矩阵g，该产流矩阵的一个维度代表时间，另一个维度则为空间即每个坡面格点的编号；

(2)根据河网与坡面的流向拓扑关系，确定每个坡面格点对应的汇流点即河道格点，并将所有的坡面格点汇总得到多流程转移矩阵t；

这里的r1格点，其对应的转移矩阵向量为(1,1,1,0,1,0,0,1)，表示有p1、p2、p3、p5、p8这5个坡面格点汇入r1；

这里的r2格点，其对应的转移矩阵向量为(0,0,0,1,0,1,1,0)，表示有p4、p6、p7这3个坡面格点汇入r2。

(3)对产流矩阵g和多流程转移矩阵t进行矩阵的内积运算，得到汇流格点的汇流矩阵r。

获取多流程转移矩阵的流程如下：

(1)判别流域内每个格点的汇流特性，是属于坡面格点还是河道格点；

(2)对于坡面格点，分析其相对于周围格点的水流方向；对于河道格点，分析有哪些坡面格点汇入该格点，从而形成多流程转移矩阵。

参照图4，具体包括如下子步骤：

(2.1)令产流格点编号j的初始值为1；

(2.2)确定第j产流格点的格点流向；

(2.3)判断第(j+1)个产流格点是否为汇流格点，若是，则确定汇流格点编号h，进入步骤(2.4)；若否，则确定下一个产流格点编号c，并进入步骤(2.2)；

(2.4)将转移矩阵的j行h列赋值为1；令j＝j+1，进入步骤(2.5)；

(2.5)判断j是否不大于产流格点数k，若是，则进入步骤(2.2)；若否，则将步骤(2.4)赋值后的转移矩阵作为多流程转移矩阵。

将汇流过程的矩阵化运算方法进一步运用到长江寸滩水文站以上流域进行分布式水文模拟中的汇流计算时，实测结果表明，在1862个时间段、216个坡面格点向95个河道格点汇流过程中，其运算时间从0.6737449秒缩短至0.02840185秒，相比于逐个格点去计算汇流过程最后再汇总所有单个格点的值，优化比高达23.7倍。

结合上述土壤基流过程的分段矩阵化运算和汇流过程的矩阵化运算实例表明，在分布式水文模型的计算过程中采用本发明提供的方法可以针对水文循环的每一个子过程进行矩阵化运算，从而可以对一个时间段内的所有格点同时进行计算，不用再逐个格点逐个时间段去运行，可以极大的提高效率，而不受限于处理器的处理能力。

本领域的技术人员容易理解，以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。