一种基于改进稀疏自动编码器的图像超分辨率方法与流程

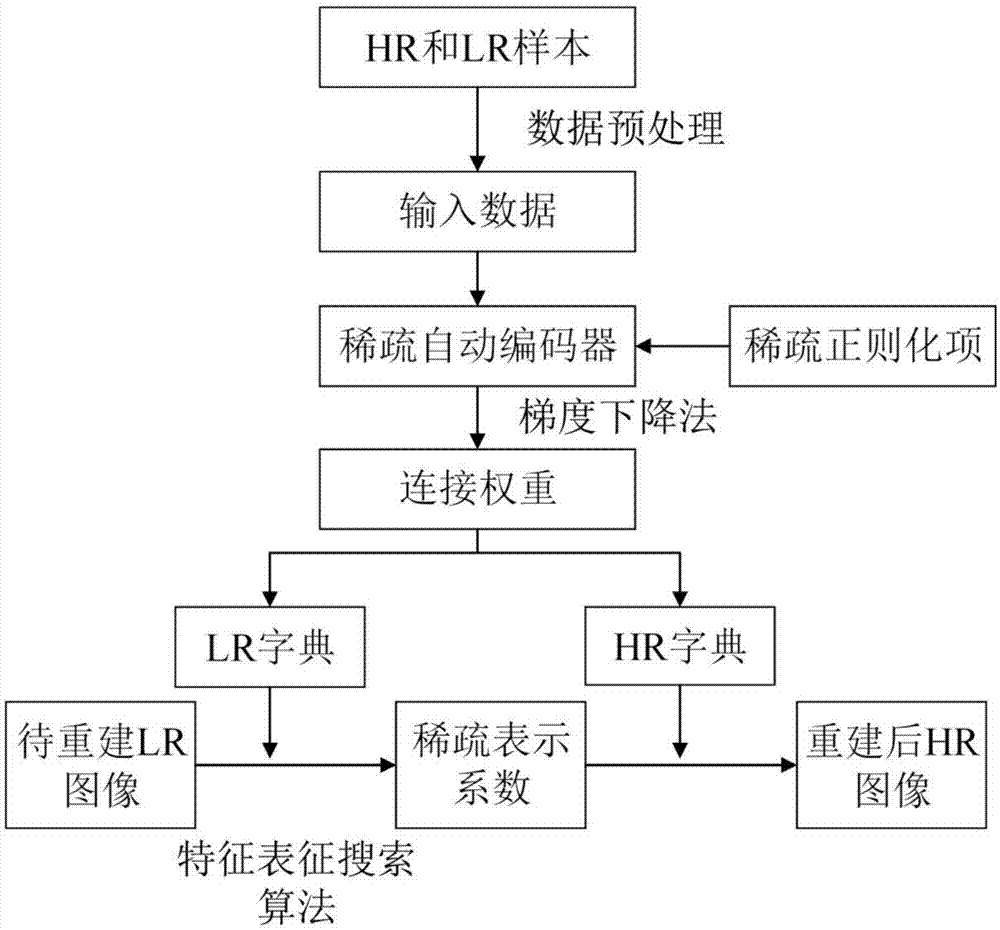
本发明涉及一种图像超分辨率方法，特别是涉及一种基于改进稀疏自动编码器的图像超分辨率方法。

背景技术：

通常，图像的空间分辨率越高意味着图像细节越丰富，越有利于后续的图像处理、分析和理解。然而，在实际应用中，由于成像设备限制、场景变化等退化因素，导致成像系统只能得到质量较差、分辨率较低的图像，不能满足实际应用的要求。图像超分辨率(superresolution,sr)方法可以利用信号处理的方法从单幅或多幅低分辨率(lowresolution,lr)图像重建出高分辨率(highresolution,hr)图像，从而提升图像的空间分辨率。因此sr方法在遥感、医疗、视频监控等领域都具有重要的应用价值。

通常，sr方法可分为3种类型：基于插值的sr方法，基于重建的sr方法和基于学习的sr方法。其中，基于学习的sr方法，作为近年来sr算法研究的热点方向，是在给定训练图像样本的基础上，通过学习的方法在hr和lr图像块之间建立确定的关系，然后利用这种关系从给定的lr图像块重建出对应的hr图像块。该类方法的关键是，在图像重建过程中引入一定的图像先验知识作为约束条件，来恢复由于图像降质损失的细节信息。

基于稀疏表示的sr方法作为基于学习的sr方法中的一种，最早由yang等提出。yang等利用自然图像的稀疏性，通过字典和稀疏表示系数的线性组合得到重建图像，从而恢复图像的高频细节；在字典学习方面，采用联合字典学习算法对hr和lr图像训练样本进行学习，使得lr图像块和对应hr图像块分别相对于lr字典和hr字典之间的稀疏表示系数是相似的，从而保证lr图像块的稀疏表示可以近似地生成hr图像块。虽然该算法可以获取充足的附加信息，恢复一定的高频细节信息，但是重建效果对字典具有强烈的依赖性，无法保证附加信息的准确性与可靠性。

技术实现要素：

有鉴于此，本发明的目的在于提供一种基于改进稀疏自动编码器的图像超分辨率方法，其利用神经网络特有的良好学习能力来实现字典学习，通过提高字典的准确性和鲁棒性来提升重建图像的质量。

为实现上述目的，本发明采用的方案是：

一种基于改进稀疏自动编码器的图像超分辨率方法，其包括以下步骤：

步骤1、以训练样本的高频信息为特征，分别构造高分辨率图像训练集和低分辨率图像训练集即hr训练集和lr训练集，然后对联合训练集进行zca白化处理；

步骤2、在传统的稀疏自动编码器代价函数中融入构造的稀疏正则化项，获取改进的稀疏自动编码器；

步骤3、采用改进稀疏自动编码器实现无监督的联合字典学习，得到包含hr字典和lr字典的字典对；

步骤4、将字典对d应用于稀疏标示超分辨率重建框架中，进行图像超分辨率重建。

所述步骤1具体如下：

步骤1.1、对hr样本图像ph下采样，得到lr图像pl；然后对pl采用双三次插值上采样，得到与hr图像相同大小的中间图像pm；

步骤1.2、构造hr训练集；

将hr样本图像ph与中间图像pm作差，去除hr图像中的低频信息，得到差值图像eh＝ph-pm，；然后对eh进行特征提取，获得hr训练集zh；

步骤1.3、构造lr训练集；

对中间图像pm采用r个高通滤波器进行滤波，i＝1,2,...,r；然后，将滤波后的图像进行特征提取，获得lr训练集zl'；接着，对lr训练集zl'采用主成分分析方法进行降维，得到lr训练集zl；

步骤1.4、结合hr训练集zh和lr训练集zl，得到联合训练集z＝[zh,zl]，其中，hr训练集表示为zh＝{z1,z2,...,zm}，lr训练集表示为zl＝{zm+1,zm+2,...,zm+n}，则联合训练集z＝[z1,z2,...,zm,zm+1,zm+2,...,zm+n]；

步骤1.5、对联合训练集z进行zca白化；

首先，对训练数据集z的协方差矩阵进行svd分解，得到特征向量矩阵u，其中，矩阵u有正交性，满足uu^t＝u^tu＝1；然后将特征向量矩阵u进行旋转，即zrot＝u^tz；将旋转后得到的矩阵zrot进行pca白化使其各个特征具有单位方差，即其中λi为矩阵zrot的协方差矩阵对角元素的值；最后，将zpcawhite,i左乘矩阵u，得到zca白化的特征其中，si∈s，zca白化后的训练集为s＝[s1,s2,...,sm,sm+1,sm+2,...,sm+n]；

步骤1.6、对zac白化后的联合训练集s进行归一化处理。

所述步骤2具体如下：

步骤2.1、构造稀疏正则化项；

结合基于字典学习的sr理论和稀疏自动编码器的模型，采用l1范数来加强对隐含层的稀疏性约束，其中，l1范数构造的正则化项为：

其中，为第l层节点j的激活量，为第l-1层节点i与第l层节点j的连接权重，为第l层节点j的偏置向量；

步骤2.2改进稀疏自动编码器代价函数，执行如下操作：

在传统稀疏自动编码器中引入构造的正则化项，即式(3)，得到如下改进代价函数：

步骤2.2、将构造稀疏正则化项融入传统的稀疏自动编码器的代价函数中，得到改进的稀疏自动编码器的代价函数为：

其中，输入数据为si∈s，s＝[s1,s2,...,sm]，输出数据为hi∈h，η＝[h1,h2,...,hm]，nl为层数，sl为第l层的节点数目，为隐含层神经元的平均激活量，λ、β和γ为正则化项参数，分别用于调整均方误差项、权重衰减项和稀疏正则项，ρ为设定好的预期激活量，其值接近于0，

步骤2.3、激活函数的选择；

在改进的稀疏自动编码器在编码阶段选用sigmoid函数作为激活函数，其表达式如式为：

改进的稀疏自动编码器的解码阶段则采用线性解码器解决数据缩放问题，线性解码器表达式为：σ(t)＝t。

所述步骤3具体如下：

结合高、低分辨率训练样本定义改进稀疏自动编码器的输入，输入数据定义为s＝[s1,s2,...,sm,sm+1,sm+2,...,sm+n]，前面m个数据属于hr训练集，后面n个属于lr训练集；

采用梯度下降法对权重和偏置量进行更新，获得输入层到隐含层的连接权重w1；

根据字典学习与神经网络表示之间的关联，学习得到的字典对应于连接权重的转置w1^t；根据输入数据，学习得到的字典可表示为d＝{w1,w2,...,wm,wm+1,wm+2,...,wm+n}，其中wi＝{w1,i,w2,i,...,wk,i}，k为字典的维数，i＝1,2,...,m+n，则hr字典为dh＝{w1,w2,...,wm}，lr字典为dl＝{wm+1,wm+2,...,wm+n}；因此，字典对表示为d＝(dh,dl)。

所述步骤4具体如下：

首先，采用特征表征搜索算法求解待重建lr图像y的稀疏编码目标函数，通过确定每一次迭代稀疏表示系数的符号来将非凸问题转变为凸问题，得到的稀疏表示系数为其表达式为：

其中，λ是用于平衡解的稀疏度和图像y保真度的参数；

然后，通过hr字典dh与稀疏表示系数线性组合，即得到重建后的图像

采用上述方案后，本发明以训练样本的高频信息为特征，分别构造高、低分辨率图像训练集，并通过zca白化技术对联合训练集去相关以降低其冗余性，从而提高自动编码器的训练效率；然后，在传统稀疏自动编码器的代价函数中加入构造的稀疏正则化项，获取改进的稀疏自动编码器，进一步加强对隐含层的稀疏性约束；接着，采用改进的稀疏自动编码器实现无监督的联合字典学习，以学习到更加准确和鲁棒的字典；最后将学习到的字典应用于基于稀疏表示的图像超分辨率重建框架中，实现图像的重建，达到提高重建质量的效果。

附图说明

图1为本发明流程图；

图2为本发明数据处理流程图；

图3a为“butterfly”整体图；

图3b为从图3a矩形框中截取的hr图像；

图3c为从图3b采样得到的lr图像；

图3d为256维数字典下的重建结果；

图3e为512维数字典下的重建结果；

图3f为1024维数字典下的重建结果；

图3g为2048维数字典下的重建结果；

图4为本发明在不同维数的字典关于set5重建图像的psnr和ssim值比较图；

图5a为“lena”整体图；

图5b为从图5a矩形框中截取的hr图像；

图5c为从图5b采样得到的lr图像；

图5d为采用l1sr方法下的重建结果；

图5e为采用sisr方法下的重建结果；

图5f为采用anr方法下的重建结果；

图5g为采用ne+ls方法下的重建结果；

图5h为采用ne+nnls方法下的重建结果；

图5i为采用ne+lle方法下的重建结果；

图5j为采用a+(16atoms)方法下的重建结果；

图5k为采用ispsr方法下的重建结果；

图5l为采用ours方法下的重建结果；

图6为本发明的sr方法与其他sr算法得到的重建图像对应的psnr和ssim比较图。

具体实施方式

如图1所示，本发明揭示了一种基于改进稀疏自动编码器的图像超分辨率方法，其包括以下步骤：

步骤1、以训练样本的高频信息为特征，分别构造高分辨率图像训练集和低分辨率图像训练集，然后通过zca(zero-phasecomponentanalysis)白化技术对联合训练集去相关以降低其冗余性，参照图2所示，

步骤1.1、对hr样本图像ph下采样，得到lr图像pl；然后对pl采用双三次插值(bicubic)上采样，得到与hr图像相同大小的中间图像pm。

步骤1.2、构造高分辨率图像训练集(hr训练集)，具体如下：

将hr图像ph与中间图像pm作差，去除hr图像中的低频信息，得到差值图像eh＝ph-pm，更好地训练表征hr图像块及其对应的lr图像块在边缘和纹理之间的关系。然后对eh进行特征提取，获得hr训练集zh。

步骤1.3、构造低分辨率图像训练集(lr训练集)，具体如下：

对中间图像pm采用r个高通滤波器进行滤波，i＝1,2,...,r，以更好地提取与高频信息相对应的局部特征。然后，将滤波后的图像进行特征提取，获得lr训练集zl'。接着，对lr训练集zl'采用主成分分析(principalcomponentanalysis,pca)方法进行降维，得到lr训练集zl。

步骤1.4、结合hr训练集zh和lr训练集zl，得到联合训练集z＝[zh,zl]，其中，m个hr训练样本表示为zh＝{z1,z2,...,zm}，n个lr训练样本表示为zl＝{zm+1,zm+2,...,zm+n}，则z＝[z1,z2,...,zm,zm+1,zm+2,...,zm+n]。

步骤1.5、对联合训练集进行zca白化；

采用zca技术降低训练集z的冗余性，从而降低训练集z中各个图像块的特征之间的相关性，使所有图像块的特征具有相同的方差。zca白化具体如下：

首先，对训练数据集z的协方差矩阵进行svd分解，得到特征向量矩阵u，其中，矩阵u有正交性，满足uu^t＝u^tu＝1。然后将特征向量矩阵u进行旋转，即zrot＝u^tz；将旋转后得到的矩阵zrot进行pca白化使其各个特征具有单位方差，即其中λi为矩阵zrot的协方差矩阵对角元素的值。最后，将zpcawhite,i左乘矩阵u，得到zca白化的特征其中，si∈s，zca白化后的训练集为

s＝[s1,s2,...,sm,sm+1,sm+2,...,sm+n](1)

在zca白化过程中，保持数据的维度，不再对数据进行降维。

步骤1.6、对zac白化后的联合训练集进行归一化处理；

由于稀疏自动编码器的输入样本需要在[0,1]之间，因此，对训练集s进行归一化处理。

步骤2、在传统的稀疏自动编码器代价函数中融入构造的稀疏正则化项，加强隐含层的稀疏性约束，获取改进的稀疏自动编码器，具体如下：

步骤2.1、构造稀疏正则化项；

稀疏自动编码器包括编码器和解码器，编码器通过非线性映射函数将输入向量x以一定的方式映射到隐含层y，而解码器负责将隐含层形成的编码y映射到输出层z，输出层具有和输入层相同的单元数，其映射关系分别如式(2)和式(3)所示，

其中，x∈[0,1]，y∈[0,1]，z∈[0,1]；w1为输入层到隐含层的权重矩阵，w2为隐含层到输出层的权重矩阵，在数值上与w1的转置相同；b1为输入层偏置向量，b2为隐含层的偏置向量；θ1＝{w1,b1}，θ2＝{w2,b2}，将参数合并，可表示为θ＝{θ1,θ2}；σ(·)为激活函数。

稀疏自动编码器通过调整参数θ使得输入与输出之间的重构误差最小，其代价函数一般采用均方误差(meansquarederror,mse)函数。通常，为了减少权值的量级并防止出现过拟合，在代价函数中增加一个权重衰减项，从而对网络的权重矩阵进行一定的限制。同时，引入一个额外项kldivergence(相对熵)来约束隐含层的稀疏性，以保证隐含层节点大部分时间处于非激活状态，即平均激活量接近于0。稀疏自动编码器的代价函数可表示为：

其中，输入数据si∈s，s＝[s1,s2,...,sm]，输出数据hi∈h，η＝[h1,h2,...,hm]，nl为层数，sl为第l层的节点数目，λ和β为正则化项参数，用于调整均方误差项和权重衰减项，为隐含层神经元的平均激活量，ρ为设定好的预期激活量，其值接近于0。

采用相对熵来惩罚显著偏离ρ的情况，如式(5)所示：

采用l1范数进一步加强对隐含层的稀疏性约束，使得隐含层中激活量接近于0的节点数量尽可能多，所构造的正则化项如式(6)所示。

其中，a为隐含层所有节点的激活值矩阵，为第l层节点j的激活量，为第l-1层节点i与第l层节点j的连接权重，为第l层节点j的偏置向量。

步骤2.2、将构造稀疏正则化项融入传统的稀疏自动编码器的代价函数中，得到改进的稀疏自动编码器的代价函数为：

其中，γ为用于调整稀疏正则项的参数。

步骤2.3、激活函数的选择。

(1)编码阶段，由于sigmoid激活函数可以将输入的数据控制在(0,1)之间，满足稀疏自动编码器的要求，而且该函数数据在传递的过程中不容易发散，且求导简单，因此，在改进的稀疏自动编码器在编码阶段选用sigmoid函数作为激活函数，其表达式如式(8)所示。

改进的稀疏自动编码器的解码阶段则采用式(9)所示的线性解码器解决数据缩放问题，更加准确地计算残差。

σ(t)＝t(9)

步骤3、采用改进稀疏自动编码器实现无监督的联合字典学习。

根据字典学习的需要，定义改进稀疏自动编码器的输入数据，执行如下操作：

考虑到联合字典学习需要在两个具有对应关系的特征空间中学习，将输入样本分为hr和lr样本两部分。任意一个隐含层均会存在一对提取hr、lr样本图像块局部特征的滤波器，如此可以实现字典的联合学习。假设hr训练样本有m个样本数据，lr训练集样本有n个样本数据，则输入数据表示为s＝[s1,s2,...,sm,sm+1,sm+2,...,sm+n]，前面m个数据属于hr训练集，后面n个属于lr训练集。对应的输出数据表示为η＝[h1,h2,...,hm,hm+1,hm+2,...,hm+n]。

采用改进稀疏自动编码器联合学习字典，执行如下操作：

首先，采用梯度下降法(gradientdescent)对权重和偏置量进行更新，获得输入层到隐含层的连接权重w1。

其次，根据字典学习与神经网络表示之间的关联，学习得到的字典对应于连接权重的转置w1^t。根据输入数据，学习得到的字典可表示为d＝{w1,w2,...,wm,wm+1,wm+2,...,wm+n}，其中wi＝{w1,i,w2,i,...,wk,i}，k为字典的维数，i＝1,2,...,m+n，则hr字典为dh＝{w1,w2,...,wm}，lr字典为dl＝{wm+1,wm+2,...,wm+n}。因此，字典对表示为d＝(dh,dl)。

步骤4、将字典对应用于稀疏标示超分辨率重建框架中，进行图像超分辨率重建。

首先，采用特征表征搜索算法求解待重建lr图像y的稀疏编码目标函数，通过确定每一次迭代稀疏表示系数的符号来将非凸问题转变为凸问题，提高稀疏表示系数的准确性，得到的稀疏表示系数为

其中，λ是用于平衡解的稀疏度和图像y保真度的参数。

然后，通过hr字典dh与稀疏表示系数线性组合，即得到重建后的图像

本发明以训练样本的高频信息为特征，分别构造高、低分辨率图像训练集，并通过zca白化技术对联合训练集去相关以降低其冗余性，从而提高自动编码器的训练效率；然后，在传统稀疏自动编码器的代价函数中加入构造的稀疏正则化项，获取改进的稀疏自动编码器，进一步加强对隐含层的稀疏性约束；接着，采用改进的稀疏自动编码器实现无监督的联合字典学习，以学习到更加准确和鲁棒的字典；最后将学习到的字典应用于基于稀疏表示的图像超分辨率重建框架中，实现图像的重建，达到提高重建质量的效果。

本发明的效果可以通过以下仿真实验进一步说明。在实验中，为了保证实验的客观性，字典学习采用91张hr训练样本，包括风景、人物和建筑等自然图像。测试图像来源于标准测试库set5和set14。实验将与bicubic、l1sr(superresolutionwithl1regression)、sisr(singleimagesuperresolution)、anr(anchoredneighborhoodregression)、ne+ls(neighborembeddingwithleastsquares)、ne+nnls(neighborembeddingwithnon-negativeleastsquares)和ne+lle(neighborembeddingwithlocallylinearembedding)、a+_16atmos(adjustedanchoredneighborhoodregression)和ispsr(improvedsuperresolutionbasedonsparserepresentation)等9种sr算法作对比。

为了定量地评价重建图像的质量，将这些测试图像作为hr参考图像，通过下采样获取待处理的lr图像。设定采样因子s＝3。在训练集预处理阶段，令r＝4，即采用4个高通滤波器，分别为f1＝[-1,0,1]，f2＝f1^t，f3＝[1,0,-2,0,1]和f4＝f3^t。在联合字典学习的过程中，与代价函数相关参数设置为：λ＝0.001，β＝6，γ＝8，ρ＝0.035；在图像重建阶段，图像子块大小为5×5。

仿真实验主要分为两组，具体如下。

第1组实验：讨论不同的字典维数(即，隐含层节点数)对重建效果的影响。

该实验将字典维数分别设为256，512，1024和2048四种情况。

图3a至图3g从主观视觉上展示了不同维数字典对应的butterfly的重建结果。采用矩形框选出对应图像中细节最为丰富的区域，以便更好地比较和分析不同sr算法对图像细节的重建效果。从图3d至图3g可以看出，当字典维数为256时，重建图像还比较模糊，边缘存在着明显的锯齿效果，当字典维数为512和1024时，重建图像的纹理和边缘逐渐改善，伪影越来越少，重建的图像越来越清晰，但是字典维数为2048时，学习得到的字典对图像的重建质量并没有明显的改善，而且学习字典的时间更长。

图4列出了不同维数的字典关于set5重建图像的psnr和ssim值。从图4可以看出，随着字典维数的增加，set5中重建图像的psnr和ssim值都逐渐增加，但是随着字典维数增加到2048，set5的大部分图像对应的重建图像的psnr和ssim值均有所下降。结合图3和图4的实验结果，字典维数为1024时，效果最好。

第2组实验：将本发明与不同sr方法比较。

为了验证本发明的效果，将算法与上述9中sr算法在psnr和ssim两个客观评价指标下进行比较。图5a和图5b展示了lena测试图像与其对应的细节图像，图5c-5l从主观视觉上展示了不同sr算法对lena的帽檐区域的重建结果。l1sr算法虽然恢复了部分细节，但是还存在明显的块效应，如图5d的脸部；sisr算法的边缘锐化效果明显，但是在重建图像中出现了部分虚假细节，如图5e中的帽子边缘；图5f-5k)对应的算法都取得较好的重建效果，但是在恢复丰富的细节信息的同时也引入了较多的虚假细节，比如这些图中lena的帽檐。本发明所提方法优于其他9种sr方法，恢复了更多的细节信息且没有引入过多的虚假细节，如图5l中lena的帽檐的重建结果都更接近于原始图像，对应的重建图像更加清晰和真实。

图6列出了不同sr算法得到的重建图像对应的psnr和ssim，其中粗体标出的数值表示在相应的评价指标下其对应算法的性能最优。由图6可见，本发明提出方法得到的psnr和ssim值大体上都是最优的，表明其的重建效果更优。

以上所述，仅是本发明实施例而已，并非对本发明的技术范围作任何限制，故凡是依据本发明的技术实质对以上实施例所作的任何细微修改、等同变化与修饰，均仍属于本发明技术方案的范围内。