简支梁结构的水平层状围岩层间粘聚力计算方法与流程

本发明属于土木工程中隧道施工技术领域，具体涉及一种考虑层间粘聚力的水平层状围岩隧道顶板安全开挖跨度计算方法中简支梁结构的水平层状围岩层间粘聚力计算方法。

背景技术：

层状岩体是一种具有层状构造的沉积岩。全世界层状岩体分布极广，约占陆地总面积的66％。我国层状岩体分布更广，达到国土面积的77％，主要集中在西南、华中和陕北等地区。层状岩体由于具有典型的层状结构，不仅变形和强度性质具有明显的各向异性，而且岩体破坏机理及方式也明显不同于其它岩体。层状岩体的变形和破坏特征主要受岩层组合和结构面控制，在施工扰动下，往往成为非常复杂的工程问题。尤其是水平层状岩体，由于结构面呈平行分布，导致其具有明显的横观各向同性，在隧道施工过程中，拱部极易出现掉块落石、离层、弯折，甚至局部坍塌、超欠挖等工程问题。拱部掉块落石是水平层状围岩隧道施工中的通病，严重威胁施工安全，导致人员伤亡、成本增加、工期延误。

随着我国交通事业的飞速发展，出现了大量的隧道工程，不可避免地会遇到水平层状围岩隧道，如太古高速的西山隧道、常吉高速的雀儿溪隧道、渝利铁路的火风山隧道等。经过多年科技攻关和工程实践，积累了一些经验，取得了一些科研成果，但水平层状围岩隧道施工中的工程问题仍然未得到有效解决。究其原因，主要是对水平层状围岩隧道顶板受力特性缺乏深入研究，没有建立合理的水平层状围岩隧道力学计算模型。与普通岩石隧道相比，水平层状围岩隧道的拱顶稳定性至关重要，而且水平层状围岩具有明显的水平层状结构和层状组合特征，各岩层间的力学性状差异远远超过它们在层厚方面的差别，和单层结构相比，层间粘聚力较强。因此，建立合理的隧道顶板力学计算模型，可为水平层状围岩隧道稳定性分析提供基础，也是解决水平层状围岩隧道施工中工程问题的关键。

目前，国内外学者对水平层状围岩隧道力学计算模型进行了大量的研究。总体来看，主要采用板模型、梁模型、弹性层状半空间模型、以及摩尔-库伦准则和hoek-brown准则对隧道顶板力学行为进行分析。虽然得到了一些成果，但其在施工设计中一般均忽视了顶板岩体层间粘聚力，施工不同阶段的模型与实际吻合度不高，使得隧道施工中临界开挖跨度参数计算与实际施工现场差异较大，影响了施工成本及进度。

技术实现要素：

本发明提出了一种简支梁结构的水平层状围岩层间粘聚力计算方法，计算中充分考虑了隧道顶板力学计算模型及水平层状围岩的层间粘聚力对开挖跨度的影响，使得计算结果更符合实际工程，对水平层状围岩隧道的设计和施工有重要的指导意义，并有效降低了施工成本，提高了隧道挖掘进度。

本发明的一种简支梁结构的水平层状围岩层间粘聚力计算方法，包括以下步骤：

【1】取水平层状围岩开挖区域支撑顶板以上的两层岩体样品，分别测量得到上层岩体的弹性模量为e1和下层岩体的弹性模量为e2，在e2<e1的情况下，按照步骤【2】和步骤【3】计算层间粘聚力g_简支；

【2】将上层岩体和下层岩体分别等效为简支梁结构支撑的上层梁和下层梁，并按照现场施工的实际参数分别计算上层梁的荷载q上、下层梁的荷载q下、上层梁的挠度ω上和下层梁的挠度ω下，其中

q上＝q1+γ1h1+g_简支；

q下＝q1+γ1h1+γ2h2-g_简支；

式中，q1为围岩竖向作用力，上层岩层厚度为h1，容重为γ1，下层岩层厚度为h2，容重为γ2，g_简支为简支梁结构的层间粘聚力；上层梁惯性矩为i1，下层梁惯性矩为i2，b1为上层梁的纵向长度，b2为下层梁的纵向长度，a为顶板岩体开挖跨度，x为顶板梁截面所建立的局部坐标系中的x轴坐标值；

【3】在协同变形条件下，上层梁的挠度ω上和下层梁的挠度ω下相同，计算得到

即为简支梁结构的层间粘聚力。

上述简支梁结构的水平层状围岩层间粘聚力计算方法，步骤【2】中

q1＝γh

h＝0.45×2^s-1ω

其中h为隧道荷载的等效高度，γ为围岩的重度(kn/m³)，s为围岩级别，ω为宽度影响系数，ω＝1+i(b-5)；i为b每增加1m时的围岩压力增加率，b为隧道宽度，b＜5m时，取i＝0.2；b＞5m时，取i＝0.1。

本发明具有的有益技术效果如下：

(1)本发明结合常规隧道施工的具体过程，将不同的施工阶段的隧道顶板力学计算模型等效为开挖初始阶段的锚固梁模型与开挖扰动后的简支梁模型，使得模型更加符合隧道的实际施工过程。

(2)本发明针对目前隧道施工中开挖宽度计算理论模型和实际施工差别较大的问题，分析了现有开挖宽度计算理论模型中存在的问题，创新地提出了水平层状围岩层间粘聚力的计算模型及粘聚力的具体计算公式；通过在传统的开挖宽度模型中植入水平层状围岩层间粘聚力的理论模型，得到了与实际施工相一致的水平层状围岩隧道顶板临界开挖跨度，对于指导水平层状围岩隧道的设计与施工具有重要的意义。

(3)本发明的层间粘聚力模型简单易懂，且推导出的隧道顶板临界开挖跨度公式以及中间过程公式中的字母意义明确，相关参数易于获取，具有较强的可操作性，并通过与实际工程(大梁峁隧道)监测的变形与受力参数比对分析，验证了模型的正确性。

附图说明

图1为本发明在隧道开挖初始阶段围岩剖面示意图；

图2为本发明在隧道挖掘中间阶段围岩剖面示意图；

图3为本发明在隧道挖掘后期阶段围岩剖面示意图；

图4为本发明隧道围岩锚固梁模型梁体受力简图；

图5为本发明隧道围岩锚固梁模型梁体剪力图；

图6为本发明隧道围岩锚固梁模型梁体弯矩图；

图7为本发明隧道围岩梁体模型等效截面坐标系轴图；

图8为本发明隧道围岩简支梁模型梁体受力简图；

图9为本发明隧道围岩简支梁模型梁体剪力图；

图10为本发明隧道围岩简支梁模型梁体弯矩图。

附图标记为：3—裂缝；4—隧道轮廓；5—上层岩体；6—下层岩体。

具体实施方式

为了使本发明的目的及优点更加清楚明白，以下结合附图及工程实例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。

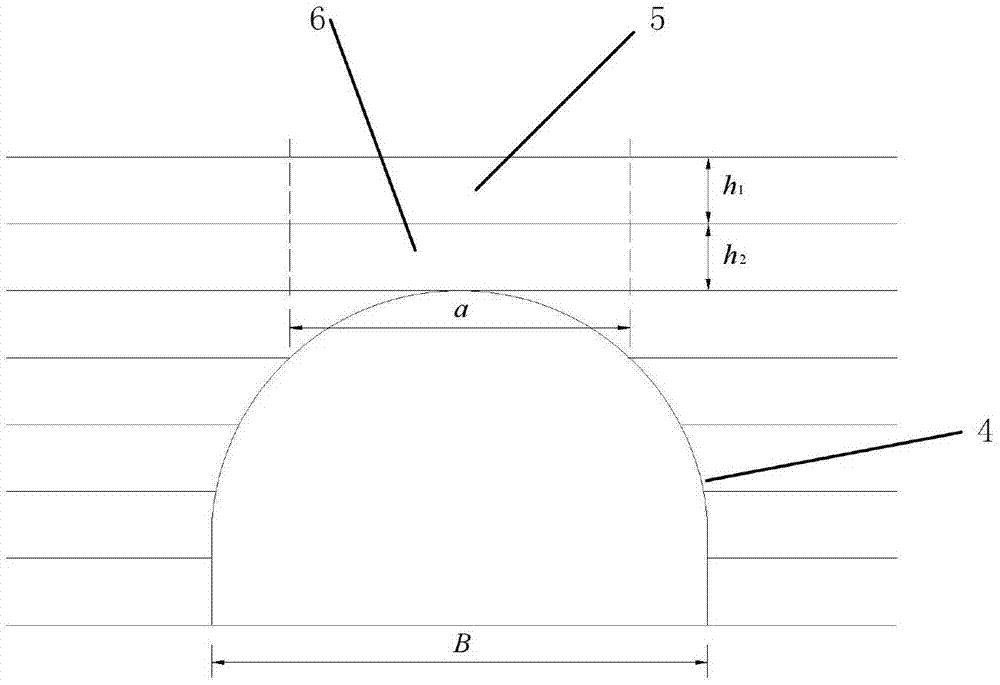
图1-3给出了隧道开挖初始阶段、中间阶段和后期阶段围岩剖面示意图，图中5和6分别表示上层岩体和下层岩体，3开挖中间阶段和后期阶段岩体形成的裂缝，4则表示隧道轮廓。

图1中，在隧道毛洞开挖初始阶段，围岩受到的扰动较小，隧道顶板岩体两端支撑部位岩体尚具有较好的完整性，此时顶板以上两层岩体受上下岩层约束，既不能转动，也不能上下左右移动，故可将隧道顶板岩体简化为如图1所示的锚固梁模型。进一步的，由于锚固梁在锚固端上部承受较大的拉应力，加之隧道后续爆破施工的干扰，使得锚固梁上端达到岩体的抗拉极限，进而使得该开裂从上而下开始贯通开展(如图2所示)，最终顶板两层岩体的端部均开裂贯通(如3所示)，此时两层梁体可沿各自的端部进行转动，则此时的隧道顶板可视之为简支梁模型。

需要说明的是，图中开挖跨度a和隧道宽度b没有确定的函数关系，隧道宽度b仅为隧道最大开挖线处的宽度，用于计算围岩竖向压力，而开挖跨度a是指隧道隧道顶板岩体的临空跨度，是对隧道顶板岩体的简化模拟。

在图1的锚固梁模型中，具体参数假定如下：隧道开挖跨度为b，上部开挖跨度为a；隧道开挖顶部自上而下第一层岩层厚度为h1，岩层弹性模量为e1，泊松比为μ1，粘结力为c1，容重为γ1，内摩擦角为第二层岩层厚度为h2，岩层弹性模量为e2，泊松比为μ2，粘结力为c2，容重为γ2，内摩擦角为

在传统的隧道开挖设计和模拟计算中，一般不考虑到岩层的结构对参数的影响，使得理论结果与实际产生较大的差别。本发明在计算中创新地提出了水平层状围岩层间粘聚力的计算模型及粘聚力的具体计算公式。需要作出解释的是：若e1>e2，即第一层岩层的刚度大于第二层岩层，则两层岩层之间存在粘聚力，第一层岩体受到向下的粘聚力，第二层岩体受到向上的粘聚力。若e1<e2，即第一层岩层刚度小于第二层岩体层岩层，则第一层岩层会对第二层岩层产生向下的附加力，此时不存在粘聚力，故本例仅对e1>e2的情况进行考虑。

首先分析上层岩层的受力情况。开挖初期围岩处于较小的扰动状态，故将此时的隧道顶板模型简化为锚固梁模型，其受力简图如图4所示。作用在等效梁体上的竖向均布荷载q(kn/m²)是由围岩的竖向作用力q1(kn/m²)、岩层自重应力q2(kn/m²)和层间粘聚力为g(kn/m²)叠加而成。水平方向上的作用力则是围岩的水平围岩压力q3(kn/m²)。竖向均布荷载q在等效梁体上作用产生的剪力如图5所示，弯矩如图6所示。

进一步的，对q1、q2、q3进行具体求解：

对q1进行求解如下：

q1＝γh

h＝0.45×2^s-1ω

式中：h为隧道荷载的等效高度，γ为围岩的重度(kn/m³)；s为围岩级别；ω为宽度影响系数，ω＝1+i(b-5)；i为b每增加1m时的围岩压力增加率，b为隧道宽度，b＜5m时，取i＝0.2；b＞5m时，取i＝0.1。

对q2进行求解如下：

q2＝γ1h1

q3＝λq1

式中：λ为侧压力系数；为围岩计算摩擦角(°)。

则作用在等效梁体上的竖向均布荷载q为：

q＝q1+q2+g

进一步分析等效梁的内力，在图4的等效梁的跨中截面(1-1)处

式中：m1-1为跨中截面(1-1)处的弯矩(kn·m)；iz为跨中截面(1-1)的惯性矩；σ1-1为跨中截面(1-1)处的正应力；f1s为该截面所受的剪力(kn)；其他符号同前。y为等效截面上的坐标系轴，参见图7。

当y取最大值，即ymax＝h1/2时，弯矩产生的正应力也是最大值，则在截面(1-1)的上缘和下缘正应力为：

式中σ1-1压为截面上缘压应力，σ1-1拉为截面下缘拉应力。

作用在等效梁跨中截面(1-1)上缘的最大正应力

σ1-1上＝σ1-1压+q3

作用在等效梁跨中截面(1-1)下缘的最大正应力σ1-1下为：

σ1-1下＝σ1-1拉-q3

而图4中等效梁的端部截面(2-2)处

式中：m2-2为端部截面(2-2)处的弯矩(kn·m)；iz为端部截面(2-2)的惯性矩；σ2-2为端部截面(2-2)处的正应力；f2s为该截面所受的剪力(kn)；其他符号同前。

当y取最大值，即ymax＝h1/2，弯矩产生的正应力也应是最大值，则在等效梁端部截面(2-2)的上缘和下缘正应力为：

式中σ2-2拉为截面上缘拉应力，σ2-2压为截面下缘压应力。

作用在等效梁端部截面(2-2)上缘的最大正应力σ2-2上为：

σ2-2上＝σ2-2拉-q3

作用在等效梁端部截面(2-2)下缘的最大正应力σ2-2下为：

σ2-2下＝σ2-2压+q3

在等效梁端部截面(2-2)处的剪应力为：

式中f2s为等效梁端部截面(2-2)所受的剪应力，等效梁端部截面(2-2)对中性轴的静矩，其它符号同前。

最大剪应力在端部截面(2-2)中心处即y＝0时，剪应力为：

以上计算可以看出，通过锚固梁的实际受力计算可知在锚固处受到的作用力最大。而且，由于岩体的抗拉强度远小于抗压强度，所以在开挖后期受到爆破施工的影响，较大拉应力的锚固端上部的岩体最先达到受拉破坏，产生如图2和图3所示的开裂，从而使隧道顶板力学模型向简支梁转化。

简支梁模型的受力简图如图8所示，剪力图如图9所示，弯矩图如图10所示。

在简支梁模型中，受力分析过程与锚固梁相同。锚固梁模型和简支梁模型不同部位的应力值见下表所列：

进一步的，对两种梁模型的层间粘聚力进行计算。

假定两层梁为协同变形状态，即其挠度相同。根据结构力学理论，锚固梁挠度公式为：

其中a为顶板岩体开挖跨度，x为顶板梁截面所建立的局部坐标系中的x轴坐标值。

上层梁受到的荷载q上为竖向地层压力q1、自重应力γ1h1和粘聚力g的合力为：

q上＝q1+γ1h1+g

下层梁受到的荷载q下为竖向地层压力q1+γ1h1、自重应力γ2h2和粘聚力g的合力为：

q下＝q1+γ1h1+γ2h2-g

上层梁挠度为：

下层梁挠度为：

根据协调变形条件(上下层梁挠度相同)，得出粘聚力g_锚固为：

将上层梁惯性矩和下层梁惯性矩分别代入上式，可得粘聚力g_锚固为：

简支梁挠度公式为：

上层梁的挠度为：

下层梁的挠度为：

与锚固梁模型同理，根据协调变形条件(上下层梁挠度相同)，得出粘聚力g_简支为：

根据以上针对隧道施工阶段不同的梁模型受力计算分析，在锚固梁锚固端截面的顶边、简支梁跨中截面的底边所受的拉应力最大，随着荷载的逐渐施加，相应部位最先达到岩体的抗拉极限强度，亦即最先达到破坏。在其破坏时的临界跨度，即可以通过相应的临界状态计算。

根据结构力学理论，锚固梁顶板临界荷载为

锚固梁顶板临界跨度为

简支梁跨中底边临界荷载为

简支梁顶板临界跨度为

最后，结合工程实际对所提出的临界开挖跨度公式进行验证。

围岩相关参数如下：

需要说明的是，在隧道临界开挖跨距计算中，要充分考虑开挖初期和开挖后期阶段锚固梁和简支梁两种模型情况下的要求，要确保开挖跨距的理论计算值，能同时满足两种模型结构的要求。通常情况下，临界跨度取两种模型中的理论计算的最小值。

下面给出具体的验证实例：

大梁峁隧道为分离式隧道，对应围岩为iv级；根据现场地质素描情况，取顶板上层岩体砂岩h1＝0.5m，下层岩体泥岩h2＝0.05～0.1m，梁的纵向宽度b取单位长度1m；下层岩体极限抗拉强度[σt]＝0.7mpa。e1＝10gpa，e2＝5gpa。计算得到两种梁模型的临界跨度，结果见下表所列。

计算结果表明：考虑层间粘聚力时，锚固梁模型临界开挖跨度为3.36～4.75m，简支梁模型临界开挖跨度为2.74～3.88m；两种模型下该隧道的最小临界跨距为2.74m。而不考虑层间粘聚力时，锚固梁模型顶板临界开挖跨度为0.14～0.30m，简支梁模型临界开挖跨度为0.12～0.24m。而实际施工中，大梁峁隧道在开挖跨度3～6m时，拱顶出现平顶现象，产生离层和掉块等超过临界跨距才有的状况，说明本发明考虑层间粘聚力的顶板力学计算模型更符合工程实际情况，其计算得到的最小临界跨距2.74m与实际的临界开挖跨度相吻合。而传统的不考虑层间粘聚力时的计算模型则与实际工程差距较大，故本发明的计算方法对于指导水平层状围岩隧道的设计与施工具有重要的意义。