温排水原型观测水域本底水温计算方法、装置及存储介质与流程
本申请涉及水域温排水检测技术领域,特别是涉及一种温排水原型观测水域本底水温计算方法、装置、计算机设备和存储介质。
背景技术:
随着时代的发展,温排水对水域环境的影响逐渐受到人们的关注,常用遥感方法对温排水排放受纳水域进行温度场观测,进而确定温排水造成的温升区影响范围。而根据遥感方法确定温排水造成的温升区影响范围的一个重要环节为确定无温排水影响下的水域本底水温。
以往确定无温排水影响下的水域本底水温的方法主要有两种,一种是人为预分割温排水温升区方法,该方法是依据温升区外围若干点温度得到温升区基准水温分布,因为温升区选取具有随意性,温升区外围点温度可能受到温排水影响,外围点温度与未受温排水影响的水温不一定相符,以此确定的无温排水影响下的水域本底水温是不准确的。第二种是采用温排水影响区域外的某一区域的平均水温作为无温排水影响下的水域本底水温,该方法忽略了水域自然水温的空间变化,以此确定的无温排水影响下的水域本底水温也是不准确的。
技术实现要素:
基于此,有必要针对上述技术问题,提供一种能够准确确定无温排水影响下的温排水原型观测水域本底水温计算方法、装置、计算机设备和存储介质。
一种温排水原型观测水域本底水温计算方法,所述方法包括:
利用通过卫星获得的工程运行后温排水原型观测期间的气象参数、水文参数、温排水取水和排水源汇项及预设的水域模型网格,确定工程运行后温排水原型观测期间的数学模型的第一输入边界条件;
根据所述第一输入边界条件、工程运行后温排水原型观测期间的实测水动力和水温结果,对所述数学模型进行率定,得到所述数学模型的合理参数取值;其中,所述数学模型包括连续方程、动量方程、物质输运方程及热交换方程,用于模拟水域的水动力和水温分布规律;
根据所述数学模型的合理参数取值及工程运行后温排水原型观测期间的数学模型的第二输入边界条件,计算待检测水域的本底水温;其中,所述第二输入边界条件是根据卫星获得的工程运行后温排水原型观测期间的气象参数、水文参数及所述水域模型网格所确定。
一种温排水原型观测水域本底水温计算装置,所述装置包括:
确定模块,用于利用通过卫星获得的工程运行后温排水原型观测期间的气象参数、水文参数、温排水取水和排水源汇项及预设的水域模型网格,确定工程运行后温排水原型观测期间的数学模型的第一输入边界条件;
数学模型率定模块,用于根据所述第一输入边界条件、工程运行后温排水原型观测期间的实测水动力和水温结果,对所述数学模型进行率定,得到所述数学模型的合理参数取值;其中,所述数学模型包括连续方程、动量方程、物质输运方程及热交换方程,用于模拟水域的水动力和水温分布规律;
计算模块,用于根据所述数学模型的合理参数取值及工程运行后温排水原型观测期间的数学模型的第二输入边界条件,计算待检测水域的本底水温;其中,所述第二输入边界条件是根据卫星获得的工程运行后温排水原型观测期间的气象参数、水文参数及所述水域模型网格所确定。
一种计算机设备,包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序,所述处理器执行所述计算机程序时实现以下步骤:
利用通过卫星获得的工程运行后温排水原型观测期间的气象参数、水文参数、温排水取水和排水源汇项及预设的水域模型网格,确定工程运行后温排水原型观测期间的数学模型的第一输入边界条件;
根据所述第一输入边界条件、工程运行后温排水原型观测期间的实测水动力和水温结果,对所述数学模型进行率定,得到所述数学模型的合理参数取值;其中,所述数学模型包括连续方程、动量方程、物质输运方程及热交换方程,用于模拟水域的水动力和水温分布规律;
根据所述数学模型的合理参数取值及工程运行后温排水原型观测期间的数学模型的第二输入边界条件,计算待检测水域的本底水温;其中,所述第二输入边界条件是根据卫星获得的工程运行后温排水原型观测期间的气象参数、水文参数及所述水域模型网格所确定。
一种计算机可读存储介质,其上存储有计算机程序,所述计算机程序被处理器执行时实现以下步骤:
利用通过卫星获得的工程运行后温排水原型观测期间的气象参数、水文参数、温排水取水和排水源汇项及预设的水域模型网格,确定工程运行后温排水原型观测期间的数学模型的第一输入边界条件;
根据所述第一输入边界条件、工程运行后温排水原型观测期间的实测水动力和水温结果,对所述数学模型进行率定,得到所述数学模型的合理参数取值;其中,所述数学模型包括连续方程、动量方程、物质输运方程及热交换方程,用于模拟水域的水动力和水温分布规律;
根据所述数学模型的合理参数取值及工程运行后温排水原型观测期间的数学模型的第二输入边界条件,计算待检测水域的本底水温;其中,所述第二输入边界条件是根据卫星获得的工程运行后温排水原型观测期间的气象参数、水文参数及所述水域模型网格所确定。
上述温排水原型观测水域本底水温计算方法,通过对用于模拟水域自然水温分布规律的数学模型进行工程运行后温排水原型观测期间工程水域的水动力和水温对比验证,对数学模型参数进行率定,得到数学模型的合理参数取值,根据数学模型的合理参数取值及工程运行后温排水原型观测期间的数学模型的第二输入边界条件,计算出工程运行后温排水原型观测期间的本底水温,因为考虑了物理作用机制下水域自然水温分布规律,从而可以获得更加准确真实的本底水温分布。此外,因上述方法无需估计温升区,克服了温升区选取具有随意性,温升区外围点温度可能受到温排水影响的缺点,可以得到更加准确合理的本底水温。
附图说明
图1为一个实施例中一种温排水原型观测水域本底水温计算方法的应用环境图;
图2为一个实施例中一种温排水原型观测水域本底水温计算方法的流程示意图;
图3为一个实施例中步骤201的细化步骤的流程示意图;
图4为一个实施例中步骤301的细化步骤的流程示意图;
图5为一个实施例中步骤202的细化步骤的流程示意图;
图6为一个实施例中步骤203的细化步骤的流程示意图;
图7为一个实施例中一种温排水原型观测水域本底水温计算装置的结构框图;
图8为一个实施例中水域模型网格示意图;
图9为水文测验测流点和潮位测点分布图;
图10为潮位验证结果示意图;
图11为流场验证结果示意图;
图12为高平潮模型计算结果与遥感温度场的比对示意图;
图13为低平潮模型计算结果与遥感温度场的比对示意图;
图14为v1-v9测点的模型计算的表层水温差值与实测的表层水温差值的统计分布示意图;
图15为大、中、小潮各特征潮态的各测点表层水温对比示意图;
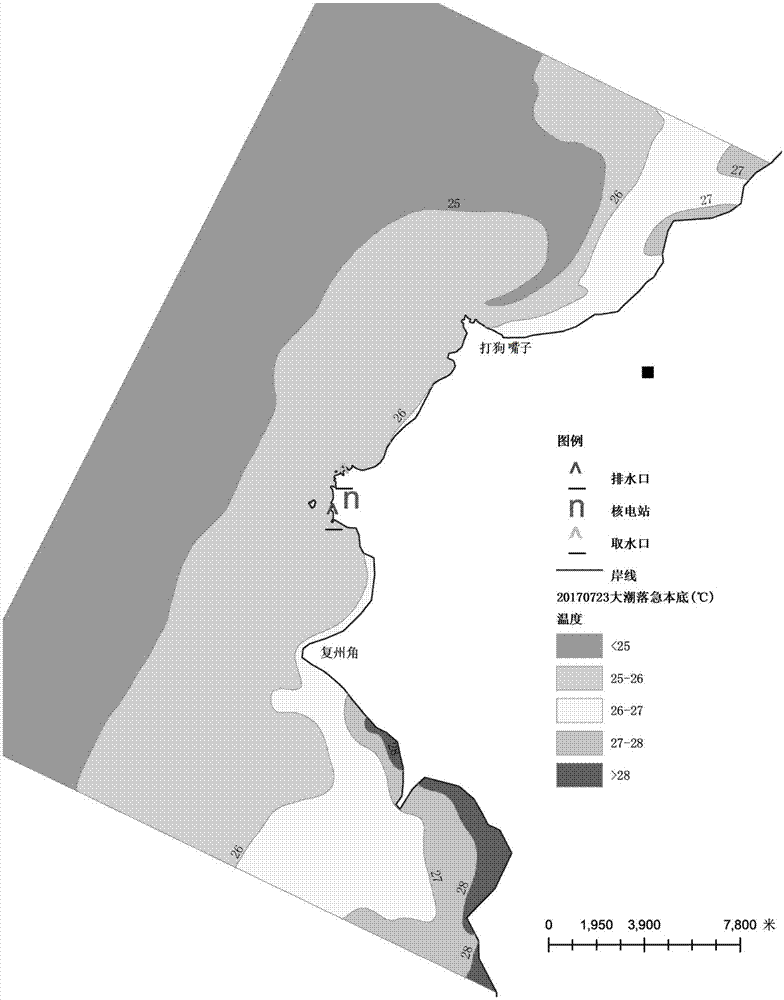
图16为利用工程运行后温排水原型观测期间的数学模型得到的本底水温分布示意图;
图17为利用卫星遥感测量的有温排水情况下绝对温度场分布示意图;
图18为温排水温升场分布示意图;
图19为一个实施例中计算机设备的内部结构图。
具体实施方式
为了使本申请的目的、技术方案及优点更加清楚明白,以下结合附图及实施例,对本申请进行进一步详细说明。应当理解,此处描述的具体实施例仅仅用以解释本申请,并不用于限定本申请。
本申请提供的水域本底水温计算方法,可以应用于如图1所示的应用环境中。其中,数据采集装置10与计算机设备20相连接。可选的,该数据采集装置是卫星,利用卫星可以获得大范围且准确的气象水文遥感数据。可选的,该计算机设备20包含至少一个处理器21与存储器22。可选的,该处理器21可以为cpu(centralprocessingunit,中央处理器)、ipu(intelligenceprocessingunit,智能处理器)等等。可选的,该处理器21可以为单核处理器或多核处理器。
其中,该计算机设备20的存储器22内包括工程运行后温排水原型观测期间的数学模型,该工程运行后温排水原型观测期间的数学模型可以选择不同的方程形式和软件进行模拟。可选的,本申请中的数学模型的控制方程包括连续方程、动量方程、物质运输方程及热交换方程。
在一个实施例中,如图2所示,提供了一种温排水原型观测水域本底水温计算方法的流程示意图,以该方法应用于图1中的计算机设备20为例进行说明,包括以下步骤:
步骤201,利用通过卫星获得的工程运行后温排水原型观测期间的气象参数、水文参数、温排水取水和排水源汇项及预设的水域模型网格,确定工程运行后温排水原型观测期间的数学模型的第一输入边界条件;
其中,工程运行后温排水原型观测期间的气象参数、水文参数是利用卫星获取到卫星数据,卫星数据采用美国国家气象环境预报中心(ncep)的气象预报系统再分析资料(csfr),资料的最小时间分辨率为1小时,水平分辨率最高达0.2度。
其中,工程运行后温排水原型观测期间的气象参数包括:气温、湿度、风速、风向、太阳辐射、大气辐射、云量、气压等时空分布。工程运行后温排水原型观测期间的水文参数包括:水温、径流量等时空分布等。其中,水域模型网格采用了一种多层次远近区嵌套网格,该网格将水域分成多个区域,如图8所示,将待检测水域分为4个区域,分别为区域①、区域②、区域③及区域④。
其中,第一输入边界条件包括:流场边界条件和温度场边界条件。流场边界条件包括:水位开边界、流场初始场、底部摩擦、水面摩擦、取水和排水源汇项等。可选的,水位开边界采用潮位边界;流场初始场采用静流条件计算;底部摩擦是根据待检测水域的底床类型确定;水面摩擦是利用水面风应力计算得到的,水面风应力表示为:
式(2-1)中,ρa表示空气密度,cd表示风拖曳力系数,u10表示自由表面以上10m的风速。
其中,温度场边界条件包括:岸边界、底部边界、开边界、自由表面、温度初始场、温排水取水和排水源汇项等。可选的,岸边界和底部边界采用绝热边界表示;开边界采用环境水温表示;自由表面采用海洋热通量模型计算表示;温度初始场采用环境水温场作为初始场;温排水取水和排水源汇项根据给定的流量和温度值确定热通量,其中取水温度为取水所在计算网格的计算温度值,排水温度为取水温度加上给定的取排水温差值。其中,取水和排水源汇项为给定流量。
需要说明的是,上述水域包括海域等,指江、河、湖、海从水面到水底的一定范围。
步骤202,根据第一输入边界条件、工程运行后温排水原型观测期间的实测水动力和水温结果,对数学模型进行率定,得到数学模型的合理参数取值;其中,数学模型包括连续方程、动量方程、物质输运方程及热交换方程,用于模拟水域的水动力和水温分布规律;
其中,工程运行后温排水原型观测期间的实测水动力和水温结果包括:工程水域固定点上的实测潮流流速、流向、水位和实测水温时间系列值。
其中,该数学模型的模拟过程为:
先利用连续方程和动量方程模拟出水域水动力场,再基于水动力场结果,利用物质运输方程及热交换方程可以模拟出水温场。该模型模拟得到的水动力场和水温场可能不准确,需要利用实测的水动力和水温值对数学模型进行参数率定,得到能准确模拟工程水域水动力和水温分布的数学模型的参数合理取值。
其中,数学模型是基于boussinesq和垂向静水压力假定的,模拟过程中采用三维曲线坐标系,其三维曲线坐标系中的垂向坐标表示如下:
式(2-2)中,d为参考平面以下的水深值,h为全水深,z为物理空间垂向坐标,ζ为自由表面高程,在底层σ=-1,表层σ=0。
其中,连续方程为:
式(2-3)中,t为时间,ξ和η为三维曲线坐标系下的水平方向的坐标,gξξ、gηη为三维曲线坐标系转换为直角坐标系的转换系数,u为ξ方向的垂向平均流速,v为η方向的垂向平均流速,q表示源汇项。
动量方程为:
在式(2-4)及式(2-5)中,u、v、ω是曲线正交坐标系下的流速分量,f是coriolis参数,fξ为ξ方向的紊动动量通量,fη为η方向的紊动动量通量,pξ为ξ方向的水压力梯度,pη为η方向的水压力梯度,νv为垂向粘滞系数,mξ为ξ方向上动量的源汇项,mη为η方向上动量的源汇项。
在浅水假定下,垂向动量方程简化为静水压方程:
其中,p表示压力,g表示常数,ρ表示水体密度。
积分后静水压表示为:
其中,patm表示大气压力。
需要说明的是,在模拟中,采用斜压模型,水体密度ρ为温度和盐度的函数,采用unesco状态方程表示,每个求解步骤通过状态方程求温度和盐度的分布引起的密度差,在压力项p中予以反映。
在σ坐标系下垂向流速ω通过连续方程求解:
式(2-8)中,垂向流速ω定义在等σ平面上,表示相对于σ平面的垂向运动。
其中,在求解fξ和fη时,涉及到水平粘滞系数νh,其表达式为:
νh=ν2d+ν3d+νmol(2-9)
其中,式(2-9)中,νmol为分子粘性系数,ν2d为水平方向未求解的亚格子水平紊动相关的紊动粘滞系数,delft3d中可以通过gui用户界面设置ν2d为全场恒定值或者随空间变化的值,也可以通过hles方法求解。ν3d为三维紊动有关的紊动粘滞系数,可通过紊流模型求解,其中,delft3d提供了prandtl混合长模型,模型为k-l模型和k-ε模型。
其中,垂向粘滞系数νv的表达式为:
νv=νmol+max(νback,ν3d)(2-10)
其中,式(2-10)中,νback为垂向粘性系数背景值,主要反映其它未求解的掺混效应(如分层流中的内波影响)。
上述方程是水动力数学模型的组成部分,利用上述方程及物质运输方程及热交换方程可以模拟水域水温分布。
其中,物质运输方程为:
式(2-11)中,c为水温,dh为水平扩散系数,dv为垂向扩散系数,λd为物质衰变系数(/day),λd的确定方法类比水流粘滞系数,s为源汇项
在求解物质运输方程时,需要考虑水体自由表面与大气之间的热交换。水体吸收的热量来源于太阳辐射和大气辐射,水体往外传输热量主要通过水体辐射、蒸发和对流散热。热交换方程需要利用热通量计算公式,不同模型采用的热通量计算公式常数取值略有不同,要求输入的气象参数有所差别,可以通过试算合理选用。
自由表面总的热通量qtot采用下式计算:
qtot=qsn+qan-qbr-qev-qco(2-12)
式(2-12)中,qsn为太阳辐射通量,qan为大气辐射通量,qbr为水体向外辐射通量,qev为蒸发散热通量,qco为对流散热通量。各分项热通量计算公式如下:
(1)净太阳辐射热通量qsn:
qsn=(1-α)qsc(1.0-0.4fc-0.38fc2)(2-13)
式(2-13)中,α为反射系数,取0.06,fc为云量系数,qsc为晴空条件下太阳辐射通量,qsc计算公式为:
式(2-14)中,s为太阳常数,取值1368[j/m2s],γ为太阳高度角,与地理纬度和时间有关。
(2)净长波辐射qeb:qeb=qbr-qan(2-15)
在海洋热通量模型中,将大气向水体的辐射和水体向外辐射认为都是长波辐射的一部分,两者合并为净长波辐射通量qeb。
qeb采用下式计算:
式(2-16)中,ε为发射系数,σ为stefan-boltsman常数,取值5.67×10-8[j/m2sk4],t为表面水温[k],ea为水汽压,fc为云量系数。
(3)蒸发散热qev:
qev=qev,forced+qev,free(2-17)
其中,qev,forced为强迫蒸发散热通量,由风驱动,qev,free为自由蒸发散热通量,由大气边界层内密度差引起的浮力作用驱动。
其中,强迫蒸发散热通量采用下式计算:
qev,forced=lvρaceu10{qs(ts)-qa(ta)}(2-18)
式中lv为蒸发潜热[j/kg],lv=2.5*106-2.3*103ts,ρa为空气密度,qs为饱和空气比湿度,qa为10m高空气比湿度,ce为dalton数,取值0.0015,u10为风速函数。
其中,自由蒸发散热通量采用下式计算:
式(2-19)中,ks为热传导系数,
(4)对流散热
海洋热通量模型中对流散热亦分为强迫对流散热qco,forced和自由对流散热qco,free,对流散热总量为两部分之和:
qco=qco,forced+qco,free(2-20)
强迫对流散热通量qco,forced采用下式计算:
qco,forced=ρacpchu10(ts-ta)(2-21)
式中ρa为空气密度,cp为空气比热,取值1004.0[j/kgk],ch为stanton数,取值0.00145,ts为水面温度,ta为空气温度。
自由对流散热通量qco,free采用下式计算:
式(2-22)中,ks为热传导系数,
利用上述式(2-1)至式(2-22)模拟水域水动力和水温分布。
步骤203,根据数学模型的合理参数取值及工程运行后温排水原型观测期间的数学模型的第二输入边界条件,计算待检测水域的本底水温;其中,第二输入边界条件是根据卫星获得的工程运行后温排水原型观测期间的气象参数、水文参数及水域模型网格所确定。
在本发明实施例中,在需要计算待检测水域某时间段的本底水温时,首先需要对数学模型进行率定,得到数学模型的合理参数取值。在得到数学模型合理参数取值后,再次利用卫星获得的气象参数、水文参数及水域模型网格确定第二输入边界条件,并利用第二输入边界条件及前述率定的数学模型,计算出待检测水域的本底水温。
其中,气象参数、水文参数表示上述的某时间段内卫星采集的遥感数据。其中,上述时间段可以是数小时、一天、数天等。优选的,在本实施例中采用逐小时数据。
上述水域本底水温计算方法方法,通过对用于模拟水域水温分布规律的数学模型进行率定,得到数学模型合理参数取值,在此基础上计算出的本底水温,考虑了物理作用机制下水域自然水温分布规律,从而可以获得更加准确真实的本底水温。此外,因上述方法无需估计温升区,克服了温升区选取具有随意性,温升区外围点温度可能受到温排水影响的缺点,可以得到更加准确真实的本底水温。
作为一种可选的实施方式,如图3所示,为步骤201的细化步骤的流程示意图,具体包括:
步骤301,将工程运行后温排水原型观测期间的气象参数、水文参数插值到水域模型网格,得到数学模型的第三输入边界条件;
在本发明实施例中,对待检测水域进行网格划分,得到水域模型网格。之后,将气象参数、水文参数插值到水域模型网格,得到数学模型的第三输入边界条件。
其中,因水域本底水温分布的实时变化是大范围气象和水文场耦合作用的结果,受制于外海水温资料精确获取困难的问题,为了尽可能消除边界条件赋值对工程水域温度模拟结果的影响,模拟边界应尽量远离工程区,工程近区模拟重要程度高,水温模拟分辨率要求高,近区岸线精度对模拟结果影响较大。因此,对待检测水域进行网格划分,如图8所示,工程远区模型采取相对粗的网格,工程近区采用较细的网格。工程远区到工程近区采用两层过渡区,网格逐步细化。实施例中数学模型总共采用四层嵌套网格,其中工程远区模拟外海范围如图8中的①区所示,通过②区和③区过渡逐渐缩小到电厂周边工程区域④区。①区的网格平面尺度平均为5000m×5000m,②区的平面网格尺度为1100m×1100m,③区的平面网格尺度为220m×220m,④区的平面网格尺度为为44m×44m。在图8中,垂向采用σ网格,经试算分析,为了兼顾模拟精度和计算效率,垂向上最终分为6层。
步骤302,将温排水取水和排水源汇项赋值到水域模型网格,得到数学模型的温排水源汇项输入;
步骤303,将数学模型的第三输入边界条件及温排水源汇项输入组成第一输入边界条件。
在本发明实施例中,利用数学模型的第三输入边界条件、温排水源汇项输入、现有的流场边界条件算法及现有的温度场边界条件算法,确定第一输入边界条件。因为流场边界条件算法、温度场边界条件算法都为现有技术,此处不再详加赘述。
上述温排水原型观测水域本底水温计算方法,将通过卫星获得到的气象参数、水文参数插值到水域模型网格中,对数学模型参数进行了率定,利用该数学模型计算出的本底水温,考虑了物理作用机制下水域自然水温分布规律,从而可以获得更加准确真实的本底水温。此外,对整个待检测水域进行网格划分,不需要估计温升区,克服了温升区选取具有随意性,温升区外围点温度可能受到温排水影响的缺点,可以得到更加准确合理的本底水温。
作为一种可选的实施方式,如图4所示,为步骤301的细化步骤的流程示意图,具体包括:
步骤401,将工程运行后温排水原型观测期间的气象参数、水文参数进行文件格式转化,得到数学模型输入所需的文本文件;
步骤402,将文本文件插值到水域模型网格,得到数学模型的第三输入边界条件。
在本发明实施例中,采用卫星获得的气象参数、水文参数是无法直接插值到水域模型网格中的,需要对气象参数、水文参数进行格式转换,优选的,采用wgrib2软件和matlab软件将气象参数、水文参数的格式转化为数学模型所需要的文本格式,并插值到水域模型网格,得到数学模型的第三输入边界条件。
需要说明的是,在进行文件格式转化之前,需要将通过卫星获得的气象参数、水文参数与工程区岸边气象站资料进行对比校验,确认气象参数、水文参数合理性。若通过卫星获得的参数与工程区岸边气象站资料之间相差不大,则可以直接使用。若存在较大差异,可以采用插值拟合等方法对气象参数、水文参数进行适当纠正后使用。
上述水域本底水温计算方法,通过对气象参数、水文参数进行格式转换,可以得到模型输入需要的文本文件,将模型输入需要的文本文件插值到水域模型网格,可以得到数学模型的第三输入边界条件。
作为一种可选的实施方式,如图5所示,为步骤202的细化步骤的流程示意图,具体包括:
步骤501,将第一输入边界条件输入至数学模型进行求解,得到计算水动力分布和计算水温分布;
在本发明实施例中,将第一输入边界条件输入至数学模型中,运行模型,得到计算水动力分布和计算水温分布。其中,计算水动力分布和计算水温分布是运行模型后的水动力和水温的计算结果。
步骤502,比对计算水动力分布和实测水动力分布是否一致,并比对计算水温分布和实测水温分布是否一致;
在本发明实施例中,实测水动力分布和实测水温分布是测量的待检测水域的真实数据分布。
步骤503,若计算水动力分布和实测水动力分布一致,且计算水温分布和实测水温分布一致,则将工程运行后温排水原型观测期间的数学模型的参数取值确定为数学模型的合理参数取值。
在本发明实施例中,利用现有的比对方法,去比对计算数据分布与实测数据分布是否相符,可选的,现有的比对方法为比对均方根、标准差等。因为上述数据分布比对方法是现有技术,此处不加以赘述。
其中,计算数据分布就是运行模型后的水动力和水温的计算结果。若计算水动力分布和实测水动力分布一致,且计算水温分布和实测水温分布一致,则表示数学模型能够准确合理反映水动力分布和水温分布。若两者中有任意一个分布不一致,则需要调整参数取值,并重新进行求解和验证,直到计算水动力分布和实测水动力分布一致,且计算水温分布和实测水温分布一致。
其中,水动力分布验证是选取工程区附近潮位站和测流站进行潮位过程和流速过程验证,精度要满足相关的规范要求,若不满足,需要调整糙率等参数,重新运行模型直到满足相关的规范要求。具体的,水文测验测流点和潮位测点分布图如图9所示,潮位验证结果如图10所示,流场验证如图11所示,其中,流场验证主要验证流速和流向。从图10中可以看出,利用模型计算出的潮位过程相位与实测吻合良好,除部分峰、谷值偏差稍大一些,计算的潮位值大部分与实测吻合良好。从图11中的潮流测站的潮流流速和流向垂向分层验证结果可以看出,模拟的流向与实测良好吻合,流速大小与实测大部分较好吻合,说明模型能够合理反映工程水域的水动力分布。
水温分布验证分为两步,第一步验证平面分布,平面分布采用卫星遥感表面温度场进行验证,主要验证计算得到的温度场从近岸到离岸方向的分布以及顺岸方向的分布是否与实测的遥感分布一致。第二步验证水温的绝对精度,水温的绝对精度采用工程建设前水文测验的测点水温进行验证,验证计算水温的绝对精度,标准偏差在0.5℃以内。如果计算的水温分布与实测遥感水温分布不一致,或者标准偏差过大,则需要调整水平扩散系数等参数,重新运行模型直到满足相关的规范要求。
上述水域本底水温计算方法,通过比对计算水动力分布和实测水动力分布是否一致,并比对计算水温分布和实测水温分布是否一致,得到能够合理准确反映工程水域的水动力分布和水温分布的数学模型参数合理取值,在此基础上可以计算出合理的本底水温。
作为一种可选的实施方式,如图6所示,为步骤203的细化步骤的流程示意图,具体包括:
步骤601,删除第一输入边界条件中的数学模型的温排水源汇项输入,得到工程运行后温排水原型观测期间的数学模型的第二输入边界条件;
在本发明实施例中,模拟工程运行后有温排水排放情况下的水域水温时数学模型输入边界条件中包含一个温排水源汇项输入,该温排水源汇项输入是一个约束条件。删除该温排水源汇项输入后,得到模拟原观期无温排水排放的本底水温计算模型输入边界条件,即第二输入边界条件。
步骤602,将第二输入边界条件及数学模型的合理参数取值,输入至数学模型进行求解,得到工程运行后温排水原型观测期间的本底水温。
将利用步骤203中得到第二输入边界条件输入至原观期无温排水模型进行求解,可以得到待检测水域的本底水温。
上述温排水原型观测水域本底水温计算方法,通过对用于模拟水域水温分布的数学模型进行率定,得到能合理模拟水域水温分布规律的数学模型参数取值,采用此率定过的数学模型计算出的本底水温,考虑了物理作用机制下水域自然水温分布规律。此外,因上述方法无需估计温升区,克服了温升区选取具有随意性,温升区外围点温度可能受到温排水影响的缺点,因此采用本计算方法可以得到更加准确真实的本底水温。
其中,还可以利用通过卫星获得的工程运行前无温排水的气象参数、水文参数及水域模型网格确定第四边界条件;将第四边界条件输入至数学模型进行求解,得到工程运行前的水动力和水温计算结果;其中,工程运行前的水动力和水温计算结果包括工程运行前的计算水动力分布和计算水温分布。比对工程运行前的水动力和水温计算结果和工程运行前的水动力和水温实测结果是否一致;若工程运行前的水动力和水温计算结果和工程运行前的水动力和水温实测结果一致,则将工程运行前无温排水确定为目标工程运行前无温排水。其中,若工程运行前的计算水动力分布和工程运行前的实测水动力分布一致,且工程运行前的计算水温分布和工程运行前的实测水温分布一致,则表示该数学模型能够合理准确反映工程前水域的水动力分布和水温分布。利用该工程运行前无温排水数学模型计算结果与实测结果的对比,可以验证数学模型模拟无温排水下的自然水温分布的合理性,进一步说明数学模型模拟本底水温的可靠性。
在利用工程前水温观测结果进行模型验证的过程中,选取电厂运行前工程水域的遥感影像资料与模型计算结果进行了对比验证。遥感影像来源于landsat7卫星数据,卫星过境期间受云层影响的概率较大,因此只能尽量选取电厂周边云量较小的卫星影像进行对比验证。图12中给出了2005年7月28日(高平潮)的模型计算结果与遥感温度场的比对示意图,图13中给出了2006年5月28日(低平潮)的模型计算结果与遥感温度场的比对示意图,2005年7月28日的数据受到云影响,遥感温度影像中有云的部分为空白值,从遥感影像可以看出遥感温度较不均匀,相邻像素温度值跳跃较大,且有一定条带性影响。然而模型计算结果则为较为连续的温度分布。但是从图12及图13的全场绝对温度值统计,模型计算结果与遥感温度差异一般在2℃以内,考虑到遥感温度绝对精度有限,但温度相对分布能够反映水域整体温度变化的趋势,因此从温度相对分布角度可以验证出利用模型计算出的温度场(模型计算结果)相对变化是合理的。利用模型计算出的温度场与遥感温度分布对比表明:
(1)从近岸到离岸方向温度由高变低的趋势看,计算的近岸高温带宽度与遥感趋势一致。
(2)从顺岸方向温度分布看,遥感温度场在复州角以南和打狗嘴子以北两侧浅弯区始终存在较高温度带,厂址温排水影响区域复州角至打狗嘴子一带受南北两侧高温带影响,2005年7月28日高平潮温度场中,复州角南北侧高温带形成一片,打狗嘴子北侧则存在一个相对低温区,是由于向北涨潮流引起,2006年5月28日低平潮温度场,复州角南侧高温带未绕过复州角,打狗嘴子北侧高温带呈现向南发展趋势,是由于向南涨潮流引起,利用模型计算的温度场也呈现相似的分布趋势。
从上述对比结果可以看出,利用数学模型模拟的本底温度场离岸变化和顺岸变化趋势与遥感温度结果基本一致,表明模拟的温度场空间相对分布是合理的。
图14给出了图9中的v1-v9所有测点的所有测量时刻,利用数学模型计算的表层水温差值与实测的表层水温差值的统计分布,可以看出温差值大部分落在±0.5℃区间,统计分析得到计算与实测的表层水温均方根误差为0.44℃。
图15给出了大、中、小潮各特征潮态的各测点表层水温对比,可以看出模型计算的水温变化趋势总体与实测的水温变化趋势一致,上述验证结果表明模型能准确模拟出温度场分布情况。
上述温排水原型观测水域本底水温计算方法,利用该工程运行前无温排水数学模型,可以验证利用该数学模型可以准确模拟出无温排水下的水动力分布与水温分布。因工程运行前计算采用的数学模型和工程运行后温排水原型观测期间计算采用的数学模型的控制方程和模型参数取值相同,通过对工程运行前无温排水数学模型的验证提高了工程运行后温排水原型观测期间计算所采用的数学模型对目标工程水域计算的可靠性。利用可以合理反映水域自然水温分布规律的数学模型计算本底水温,因为考虑了物理作用机制下水域自然水温分布规律,从而可以获得更加准确真实的本底水温。
在本发明实施例中,如图16所示为利用经实测水温资料率定过的数学模型得到的本底水温分布示意图,如图17所示为利用卫星遥感测量的有温排水情况下绝对温度场分布示意图,利用图17的绝对温度场分布扣除图16的本底水温分布,即可以得到如图18所示的温排水温升场分布。
应该理解的是,虽然图2-6的流程图中的各个步骤按照箭头的指示依次显示,但是这些步骤并不是必然按照箭头指示的顺序依次执行。除非本文中有明确的说明,这些步骤的执行并没有严格的顺序限制,这些步骤可以以其它的顺序执行。而且,图2-6中的至少一部分步骤可以包括多个子步骤或者多个阶段,这些子步骤或者阶段并不必然是在同一时刻执行完成,而是可以在不同的时刻执行,这些子步骤或者阶段的执行顺序也不必然是依次进行,而是可以与其它步骤或者其它步骤的子步骤或者阶段的至少一部分轮流或者交替地执行。
在一个实施例中,如图7所示,提供了一种温排水原型观测水域本底水温计算装置,包括:确定模块701、数学模型率定模块702和计算模块703,其中:
确定模块701,用于利用通过卫星获得的工程运行后温排水原型观测期间的气象参数、水文参数、温排水取水和排水源汇项及预设的水域模型网格,确定工程运行后温排水原型观测期间的数学模型的第一输入边界条件;
数学模型率定模块702,用于根据第一输入边界条件、工程运行后温排水原型观测期间的实测水动力和水温结果,对数学模型进行率定,得到数学模型的合理参数取值;其中,数学模型包括连续方程、动量方程、物质输运方程及热交换方程,用于模拟水域的水动力和水温分布规律;
计算模块703,用于根据数学模型的合理参数取值及工程运行后温排水原型观测期间的数学模型的第二输入边界条件,计算待检测水域的本底水温;其中,第二输入边界条件是根据卫星获得的工程运行后温排水原型观测期间的气象参数、水文参数及水域模型网格所确定。
作为一种可选的实施方式,确定模块701具体用于:将工程运行后温排水原型观测期间的气象参数、水文参数插值到水域模型网格,得到数学模型的第三输入边界条件;将温排水取水和排水源汇项赋值到水域模型网格,得到数学模型的温排水源汇项输入;将数学模型的第三输入边界条件及温排水源汇项输入组成第一输入边界条件。
作为一种可选的实施方式,还包括网格划分模块,网格划分模块用于对待检测水域进行网格划分,得到水域模型网格。
作为一种可选的实施方式,确定模块701还具体用于:将工程运行后温排水原型观测期间的气象参数、水文参数进行文件格式转化,得到数学模型输入所需的文本文件;将文本文件插值到水域模型网格,得到数学模型的第三输入边界条件。
作为一种可选的实施方式,数学模型率定模块702具体用于:将第一输入边界条件输入至数学模型进行求解,得到计算水动力分布和计算水温分布;比对计算水动力分布和实测水动力分布是否一致,并比对计算水温分布和实测水温分布是否一致;若计算水动力分布和实测水动力分布一致,且计算水温分布和实测水温分布一致,则将工程运行后温排水原型观测期间的数学模型的参数取值确定为数学模型的合理参数取值。
作为一种可选的实施方式,计算模块703具体用于:删除第一输入边界条件中的数学模型的温排水源汇项输入,得到工程运行后温排水原型观测期间的数学模型的第二输入边界条件;将第二输入边界条件及数学模型的合理参数取值,输入至数学模型进行求解,得到工程运行后温排水原型观测期间的本底水温。
关于温排水原型观测水域本底水温计算装置的具体限定可以参见上文中对于温排水原型观测水域本底水温计算方法的限定,在此不再赘述。上述温排水原型观测水域本底水温计算装置中的各个模块可全部或部分通过软件、硬件及其组合来实现。上述各模块可以硬件形式内嵌于或独立于计算机设备中的处理器中,也可以以软件形式存储于计算机设备中的存储器中,以便于处理器调用执行以上各个模块对应的操作。
在一个实施例中,提供了一种计算机设备,该计算机设备可以是服务器,其内部结构图可以如图19所示。该计算机设备包括通过系统总线连接的处理器、存储器、网络接口和数据库。其中,该计算机设备的处理器用于提供计算和控制能力。该计算机设备的存储器包括非易失性存储介质、内存储器。该非易失性存储介质存储有操作系统、计算机程序和数据库。该内存储器为非易失性存储介质中的操作系统和计算机程序的运行提供环境。该计算机设备的数据库用于存储气象数据及水文数据。该计算机设备的网络接口用于与外部的终端通过网络连接通信。该计算机程序被处理器执行时以实现一种水域本底水温计算方法。
本领域技术人员可以理解,图19中示出的结构,仅仅是与本申请方案相关的部分结构的框图,并不构成对本申请方案所应用于其上的计算机设备的限定,具体的计算机设备可以包括比图中所示更多或更少的部件,或者组合某些部件,或者具有不同的部件布置。
在一个实施例中,提供了一种计算机设备,包括存储器、处理器及存储在存储器上并可在处理器上运行的计算机程序,处理器执行计算机程序时实现以下步骤:利用通过卫星获得的工程运行后温排水原型观测期间的气象参数、水文参数、温排水取水和排水源汇项及预设的水域模型网格,确定工程运行后温排水原型观测期间的数学模型的第一输入边界条件;根据第一输入边界条件、工程运行后温排水原型观测期间的实测水动力和水温结果,对数学模型进行率定,得到数学模型的合理参数取值;其中,数学模型包括连续方程、动量方程、物质输运方程及热交换方程,用于模拟水域的水动力和水温分布规律;根据数学模型的合理参数取值及工程运行后温排水原型观测期间的数学模型的第二输入边界条件,计算待检测水域的本底水温;其中,第二输入边界条件是根据卫星获得的工程运行后温排水原型观测期间的气象参数、水文参数及水域模型网格所确定。
在一个实施例中,提供了一种计算机可读存储介质,其上存储有计算机程序,计算机程序被处理器执行时实现以下步骤:利用通过卫星获得的工程运行后温排水原型观测期间的气象参数、水文参数、温排水取水和排水源汇项及预设的水域模型网格,确定工程运行后温排水原型观测期间的数学模型的第一输入边界条件;根据第一输入边界条件、工程运行后温排水原型观测期间的实测水动力和水温结果,对数学模型进行率定,得到数学模型的合理参数取值;其中,数学模型包括连续方程、动量方程、物质输运方程及热交换方程,用于模拟水域的水动力和水温分布规律;根据数学模型的合理参数取值及工程运行后温排水原型观测期间的数学模型的第二输入边界条件,计算待检测水域的本底水温;其中,第二输入边界条件是根据卫星获得的工程运行后温排水原型观测期间的气象参数、水文参数及水域模型网格所确定。
本领域普通技术人员可以理解实现上述实施例方法中的全部或部分流程,是可以通过计算机程序来指令相关的硬件来完成,所述的计算机程序可存储于一非易失性计算机可读取存储介质中,该计算机程序在执行时,可包括如上述各方法的实施例的流程。其中,本申请所提供的各实施例中所使用的对存储器、存储、数据库或其它介质的任何引用,均可包括非易失性和/或易失性存储器。非易失性存储器可包括只读存储器(rom)、可编程rom(prom)、电可编程rom(eprom)、电可擦除可编程rom(eeprom)或闪存。易失性存储器可包括随机存取存储器(ram)或者外部高速缓冲存储器。作为说明而非局限,ram以多种形式可得,诸如静态ram(sram)、动态ram(dram)、同步dram(sdram)、双数据率sdram(ddrsdram)、增强型sdram(esdram)、同步链路(synchlink)dram(sldram)、存储器总线(rambus)直接ram(rdram)、直接存储器总线动态ram(drdram)、以及存储器总线动态ram(rdram)等。
以上实施例的各技术特征可以进行任意的组合,为使描述简洁,未对上述实施例中的各个技术特征所有可能的组合都进行描述,然而,只要这些技术特征的组合不存在矛盾,都应当认为是本说明书记载的范围。
以上所述实施例仅表达了本申请的几种实施方式,其描述较为具体和详细,但并不能因此而理解为对发明专利范围的限制。应当指出的是,对于本领域的普通技术人员来说,在不脱离本申请构思的前提下,还可以做出若干变形和改进,这些都属于本申请的保护范围。因此,本申请专利的保护范围应以所附权利要求为准。
- 该技术已申请专利。仅供学习研究,如用于商业用途,请联系技术所有人。
- 技术研发人员:陈小莉
- 技术所有人:中国水利水电科学研究院
- 我是此专利的发明人
- 该领域下的技术专家
- 如您需求助技术专家,请点此查看客服电话进行咨询。
- 1、李老师:1.计算力学 2.无损检测
- 2、毕老师:机构动力学与控制
- 3、袁老师:1.计算机视觉 2.无线网络及物联网
- 4、王老师:1.计算机网络安全 2.计算机仿真技术
- 5、王老师:1.网络安全;物联网安全 、大数据安全 2.安全态势感知、舆情分析和控制 3.区块链及应用
- 如您是高校老师,可以点此联系我们加入专家库。
- 还没有人留言评论。精彩留言会获得点赞!