一种在最少换乘下的公共交通网络最短路径长度计算方法与流程

本发明属于公共交通领域，更具体地，涉及一种在最少换乘下的公共交通网络最短路径长度计算方法。

背景技术：

公共交通系统是为居民出行和社会物资运输提供交通服务的工程设施，在国家或地区的经济发展和人民生活中发挥至关重要的作用。在公共交通系统的规划和调度过程中，站点之间的最短路径是需要重点考虑的因素之一。而在公共交通网络中，换乘对路径长度的度量有着重要影响，不同的换乘方式往往对应着不同的路径长度，而且人们一般更希望在较少的换乘次数下到达目的地，但当前的公共交通网络最短路径长度计算大多忽视了这种换乘对路径长度的影响。

技术实现要素：

针对现有技术的以上缺陷或改进需求，本发明提供了一种在最少换乘下的公共交通网络最短路径长度计算方法，由此解决现有技术没有考虑换乘对路径长度的影响这一技术问题。

为实现上述目的，本发明提供了一种在最少换乘下的公共交通网络最短路径长度计算方法，包括：

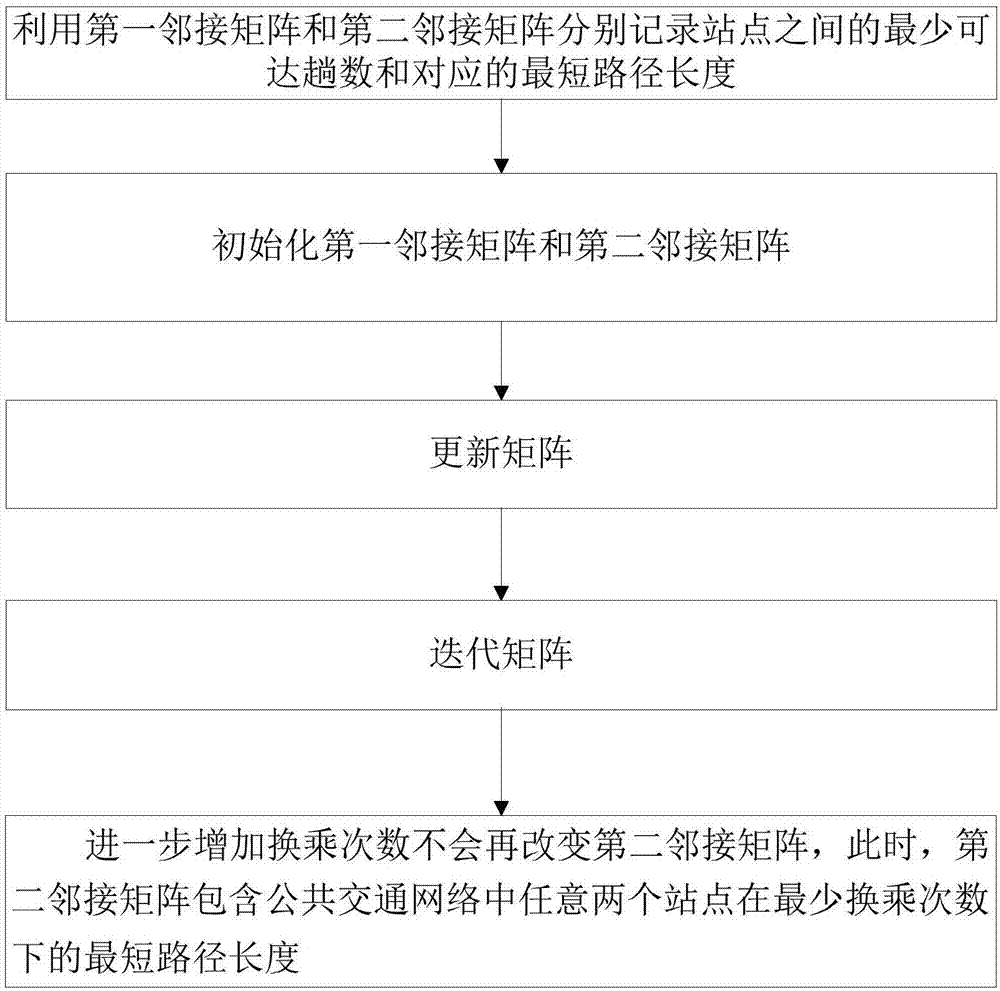
(1)利用第一邻接矩阵tk×k和第二邻接矩阵hk×k分别记录站点之间的最少可达趟数和对应的最短路径长度，第一邻接矩阵tk×k中的第一元素ti，j表示站点ni和nj之间的最少可达趟数，(ti，j-1)表示站点ni和nj之间的最少换乘次数，第二邻接矩阵hk×k中的第二元素hi，j表示站点ni和nj之间在最少换乘下的最短路径长度，k表示公共交通站点的数量，i∈[1，k]，j∈[1，k]；

(2)初始化第一邻接矩阵tk×k和第二邻接矩阵hk×k，以和表示第一邻接矩阵tk×k和第二邻接矩阵hk×k的初始状态，和中的矩阵元素和设为+∞；

(3)利用和中的矩阵元素和更新矩阵和至和

(4)基于和迭代矩阵和至和m≥2；

(5)重复步骤(4)直至即进一步增加换乘次数不会再改变第二邻接矩阵hk×k，令此时，第二邻接矩阵hk×k包含公共交通网络中任意两个站点在最少换乘次数下的最短路径长度。

进一步地，步骤(3)包括：

若ni和nj是一条公共交通线路上的两个站点，i≠j，则中的元素对于矩阵若求站点之间的最短旅行距离，则中的元素若求站点之间的最短旅行时间，则其中，v和δ分别表示公共交通工具的平均行驶速度和平均等待时间，dis(ni，nj)表示站点ni至nj的行驶距离，若ni和nj不是一条公共交通线路上的两个站点，则中的元素中的元素

进一步地，步骤(4)包括：

(4-1)对于站点ni和nj，若中的元素则中的元素中的元素

(4-2)若选择站点nx作为ni和nj之间的换乘站点，其中x≠i≠j，计算的值；

(4-3)对除ni和nj之外的所有公共交通站点重复步骤(4-2)，对于所有换乘站点nx，选择使值最小的nx作为换乘站点，如果则如果仅有一个站点nx使值最小，则该站点nx作为换乘站点，且如果存在多个站点nx使值最小，则且选择的值最小时相应的站点nx作为换乘站点。

总体而言，通过本发明所构思的以上技术方案与现有技术相比，能够取得下列有益效果：

(1)本发明引入邻接矩阵，在考虑最少换乘次数下对邻接矩阵进行迭代，考虑换乘对最短路径的影响，进而得到在最少换乘次数下的最短路径长度。本发明得到的最短路径长度更准确、可靠性更强。

(2)本发明最终可以得到在最少换乘次数下公共交通网络中任意两个站点之间的最短路径长度，包括最短旅行距离和最短旅行时间。

附图说明

图1是本发明实施例提供的一种在最少换乘下的公共交通网络最短路径长度计算方法的流程图；

图2是本发明实施例提供的公共交通网络示意图。

具体实施方式

为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。此外，下面所描述的本发明各个实施方式中所涉及到的技术特征只要彼此之间未构成冲突就可以相互组合。

如图1所示，一种在最少换乘下的公共交通网络最短路径长度计算方法，包括：

(1)利用第一邻接矩阵tk×k和第二邻接矩阵hk×k分别记录站点之间的最少可达趟数和对应的最短路径长度，第一邻接矩阵tk×k中的第一元素ti，j表示站点ni和nj之间的最少可达趟数，(ti，j-1)表示站点ni和nj之间的最少换乘次数，第二邻接矩阵hk×k中的第二元素hi，j表示站点ni和nj之间在最少换乘下的最短路径长度，k表示公共交通站点的数量，i∈[1，k]，j∈[1，k]；

(2)初始化第一邻接矩阵tk×k和第二邻接矩阵hk×k，以和表示第一邻接矩阵tk×k和第二邻接矩阵hk×k的初始状态，和中的矩阵元素和设为+∞；

(3)利用和中的矩阵元素和更新矩阵和至和

(4)基于和迭代矩阵和至和m≥2；

(5)重复步骤(4)直至即进一步增加换乘次数不会再改变第二邻接矩阵hk×k，令此时，第二邻接矩阵hk×k包含公共交通网络中任意两个站点在最少换乘次数下的最短路径长度。

进一步地，步骤(3)包括：

若ni和nj是一条公共交通线路上的两个站点，i≠j，则中的元素对于矩阵若求站点之间的最短旅行距离，则中的元素若求站点之间的最短旅行时间，则其中，v和δ分别表示公共交通工具的平均行驶速度和平均等待时间，dis(ni，nj)表示站点ni至nj的行驶距离，若ni和nj不是一条公共交通线路上的两个站点，则中的元素中的元素

进一步地，步骤(4)包括：

(4-1)对于站点ni和nj，若中的元素则中的元素中的元素

(4-2)若选择站点nx作为ni和nj之间的换乘站点，其中x≠i≠j，计算的值；

(4-3)对除ni和nj之外的所有公共交通站点重复步骤(4-2)，对于所有换乘站点nx，选择使值最小的nx作为换乘站点，如果则如果仅有一个站点nx使值最小，则该站点nx作为换乘站点，且如果存在多个站点nx使值最小，则且选择的值最小时相应的站点nx作为换乘站点。

如图2所示，假设公共交通网络有7个公共交通站点，存在三条公共交通线路：线路1(1-2-3-4)、线路2(1-2-5-3)和线路3(6-4-7)，相邻站点之间的距离如图2所示。基于上述矩阵t和h的迭代过程，通过三次迭代，可以得到该公共交通网络任意两个站点在最少换乘次数下的最短路径长度，以最少换乘次数下的最短旅行距离为例，其具体的计算结果如下：

本发明所述的最少换乘次数下的公共交通网络最短路径长度计算方法，能够在考虑最少换乘的情形下，计算得到公共交通网络中任意两个站点之间的最短路径长度，包括最短旅行距离和最短旅行时间。

本领域的技术人员容易理解，以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。