针对低亮度环境的CANNY算子边缘检测算法的制作方法

本发明涉及一种图像处理技术，特别是一种针对低亮度环境的canny算子边缘检测算法。

背景技术：

图像边缘部分是指图像在局部区周围像素灰度变化显著的部分，其广泛存在于不同物体之间及物体与背景之间。图像边缘提取就是检测出这些边缘，并将其尽量完整且不引入噪声边缘地提取出来，形成主要物体与背景的轮廓。较其他的边缘提取算子，canny算子采用了变分法，以找到一个最优的边缘检测算法。canny算子具有检测精度十分的高，能尽可能多地检测出图像的实际边缘；信噪比大，同一物体的边缘只会标识一次，不会将可能存在的噪声标记为边缘；定位准确，标识出的边缘与实际图像的边缘十分接近等优点；

canny算子的基本步骤有3步：图像滤波，边缘增强，边缘检测。边缘增强的算法主要是基于图像的一阶和二阶导数，但导数对噪声十分敏感，所以处理图像首先会对图像进行一定程度的平滑处理，以滤除噪声；在滤除噪声的基础上，通过确定图像各点领域强度的变化值，可以将图像灰度点领域强度值有显著变化的点凸显出来，达到对图像边缘的增强，通常的做法是计算梯度的幅值来确定；经过增强的图像，往往领域中有很多点的梯度值很大，检测时，会采用某种方法对这些点进行取舍，常用的方法为阈值化。

但低亮度环境下的图像，图像像素灰度值普遍很低，噪声对图像影响更大且实际边缘点梯度幅值较小，图像边缘难以检测；传统canny算子对于斜方向的边缘线条检测效果不好；且最后边缘检测的阈值需人为指定。

技术实现要素：

本发明的目的在于提供一种针对低亮度环境的canny算子边缘检测算法，包括以下步骤：

步骤1，对原始图像进行高斯平滑滤波、log变换、直方图均衡化；

步骤2，对步骤1得到的图像，在2组4个方向上分别采用sobel算子及sobel算子在斜方向上的变种，取幅值均值作为处理后的像素点数据；

步骤3，采用高低阈值方法，高于高阈值的像素点保留，反之则舍弃，保留的刑诉点组成边缘检测图像。

本发明与现有技术相比，具有以下优点：本发明提出一种在预处理前经log变换、直方图均衡处理以增强图像的细节信息，舍弃图像冗余信息；在图像增强时，增加了对斜方向梯度信息的提取；以及在最后边缘检测的阈值化时，提出多阈值自适应的方法，达到自动提取图像最优边缘地目的。

下面结合说明书附图对本发明作进一步描述。

附图说明

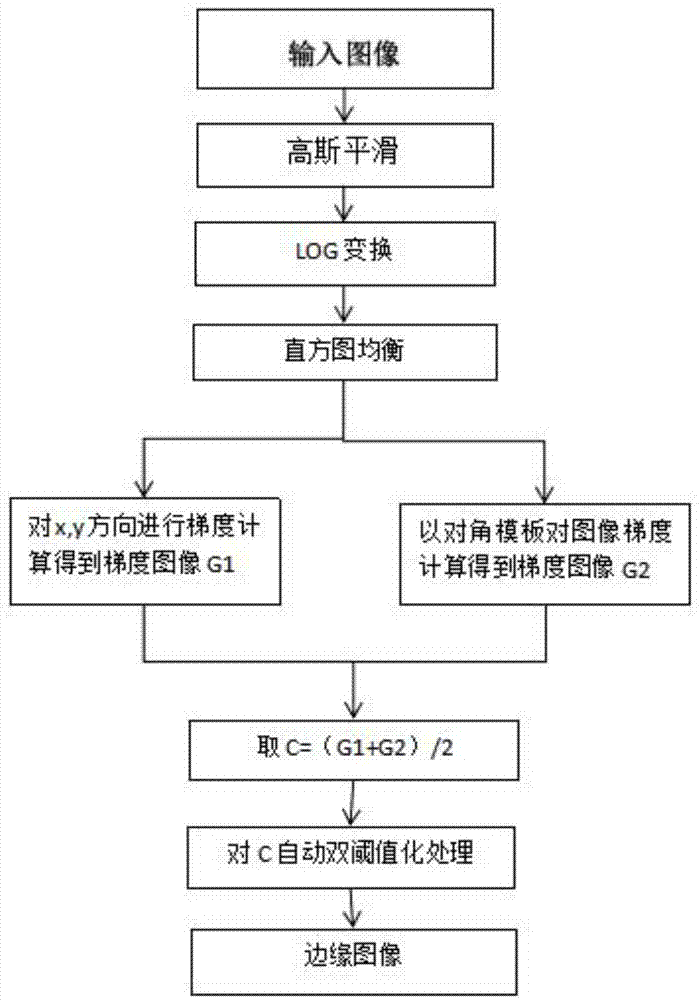
图1为整体算法流程图。

图2为5×5高斯卷积核模板示意图。

图3为3×3sobel算子对角卷积模板示意图。

图4为未经处理的原始图像示意图。

图5为经原始canny算子处理的图像示意图。

图6为经此算法处理的图像示意图。

具体实施方式

结合图1，一种针对低亮度环境的canny算子边缘检测算法，包括以下步骤：

步骤1，对原始图像进行高斯平滑滤波，以滤除高频噪声：

由于高斯滤波对抑制服从正态分布的噪声十分有效，但在实际处理过程中随着高斯模板的增大，图像会被过于平滑化导致边缘之间的界限逐渐模糊，被识别的图像边缘会逐渐减少。因此需要选择适当大小的高斯模板。一方面抑制一些伪边缘点同时保留原图像的重要边缘信息。

高斯平滑滤波函数表示如下：

通过原图像f(x,y)与高斯滤波器卷积，得到平滑后图像g(x,y)，其过程表示为：

g(x,y)＝f(x,y)*h(x,y,σ)(2)

在实际图像处理中选取适当的σ，得到的5×5高斯卷积核函数为图2所示。

步骤2，对上一步骤得到的图像进行log变换，以整体提高图像亮度和对比度，增强图像细节信息：

对于原图像f(x,y)，l(x,y)为变换后图像。

变换方法：

l(x,y)＝c*log(1+v*g(x,y))(3)

选取适当的底数及c、v的值处理各像素点。

步骤3，继续对图像进行直方图均衡化，增强局部对比度，丰富图像轮廓信息：

由于直方图均衡改变的是像素灰度级分布，其处理过程采用另一种形式表示。直方图均衡化可由下列过程表示：

把均衡化之前和之后的图像中像素灰度级分布看成f(x)和f(y),且这两个随机变量之间存在函数转换关系y＝t(x)。记f(x)、f(y)分别为f(x)、f(y)的概率密度函数，那么求t(x)的过程就是直方图均衡化过程。

首先，

其中nk为灰度为k的像素占所有像素的比例，m与n分布为图像的行数和列数；

其次

其中l为灰度级的个数，通常l＝256；

因为

f(y)＝p(y≤y)＝p(t(x)≤y)＝p(x≤t^-1(y))＝f(x)x＝t^-1(y)(6)

对上式两边的y同时求导得到

把已知和要求的部分套入上式

整理为

两边同时对x积分(在这里是求和)

步骤4，在2组(共4个)方向上分别采用sobel算子及sobel算子在斜方向上的变种，取幅值均值作为处理后的像素点数据：

sobel算子的基本公式为：

梯度的幅值与方向由下式表示，其中g为幅值，θ为方向：

2组4个方向，第一组即水平与垂直这两个方向，即x,y坐标轴。第二组即(与x轴正方向成)斜45度与斜135度这两个方向。这样做能使得到的轮廓在斜方向上的信息更丰富。

下面介绍对斜方向梯度信息的提取：

用图2所示两个3×3对角模板对图像中的像素值加权平均，实际上这是经典sobel算子在斜方向上的表示。对应对角模板1的梯度计算为

对应对角模板2的梯度计算为

取平方根得总梯度大小为

若记x、y方向上的梯度幅值为g1，斜方向上的梯度幅值为g2，则综合后的图像梯度g为

步骤5，采用高低阈值方法，阈值大小由上一步骤所得图像的灰度分布决定，阈值分为高阈值，低阈值，低于低阈值的像素点舍弃，高于高阈值的像素点保留，处于之间若其领域内有高于高阈值的像素点，则保留，反之则舍弃；最后获得边缘检测图像；最后获得边缘检测图像：

关于高、低阈值的确定：

首先求出整幅图像的灰度平均值

常规的边缘检测算法往往保留了较多的冗余信息，造成信息杂乱不精简，此算法舍弃原图像百分之30的冗余信息，故高阈值设为1.2g，低阈值为高阈值的二分之一，即0.6g。

对于处于高低阈值之间的像素点

这里的领域指定为像素点所处矩阵空间的周围一定的对称范围，阈值为1.2g。

实施例

本例选取了低亮度下的人物背景图，图4为未经处理的原始图像，图5为经典canny算子处理后的图像，图6为本算法处理后的图像。可以看出本算法处理的图像任务及背景轮廓更连续，有效信息更多且冗余信息较少。