关于多喷管火箭流场及对流/辐射耦合换热的仿真方法与流程

本发明属于超声速飞行器数值仿真领域，特别是一种关于多喷管火箭流场及对流/辐射耦合换热的仿真方法。

背景技术：

火箭发动机工作时，推进剂的燃烧产物经发动机喷管喷出形成高温高速燃气射流，会对发射管壁和箭体产生干扰，从而影响火箭发射系统的稳定性和安全性。而目前我国下一代大推力将采用多喷管的捆绑式运载火箭。捆绑式运载火箭的芯级发动机和助推器发动机同时工作时，多台发动机的喷流相互交叉，同时存在外部扰流的干扰，在火箭底部区域形成复杂流场，加剧了对火箭底部区域的加热效应。燃气射流诱导下的吸力和壁面射流相互碰撞形成反射，形成回流对流加热。高温燃气中co2、h2o等气体微粒，特别是al2o3等高温固体颗粒，会对火箭底部产生辐射加热作用。除此之外，高温燃气流过喷管，会使喷管壁温度升高，高温的喷管壁也会对火箭底部有一定的辐射加热作用。因此，对流加热和辐射加热的共同作用，将导致火箭底部温度较高，影响底部器件工作性能。

底部热环境对底部设备的安全性至关重要，热防护材料既要满足高温环境要求，又要尽可能减少结构重量和成本。火箭底部热环境的地面试验实施困难、成本巨大，随着计算流体力学的不断发展，以及计算机性能的不断提高，数值模拟已经成为研究流场的一种有效手段。negishih,yamanishin,aritam,etal.numericalanalysisofplumeheatingenvironmentforh-iialaunchvehicleduringpoweredascent[c]//aiaa/asme/sae/aseejointpropulsionconference&exhibit.2013.对日本四喷管火箭h-iia采用p-1辐射模型进行仿真，在利用30个cpu并行计算两个月的情况下，仿真结果与试验结果误差大于10％，并且随着航天科技的发展，火箭载荷增大，体积增大，导致火箭整体流场计算区域大，网格规模大，计算量增加，需要通过大规模并行计算求解，这时就迫切需要一种高精度，低计算成本的数值仿真方法模拟多喷管火箭流场及对流/耦合换热的过程。

技术实现要素：

本发明的目的在于提供一种多喷管火箭流场及对流/辐射耦合换热的仿真方法，以解决多喷管火箭喷流相互干扰难以计算的问题。

实现本发明目的的技术方案为：

一种关于多喷管火箭流场及对流/辐射耦合换热的仿真方法，包括以下步骤：

步骤1、建立多喷管火箭三维模型；

步骤2、利用多重分块结构化网格方法对三维模型进行网格划分；

步骤3、建立多喷管火箭羽流流场以及对流换热的数学模型：对n-s多组分方程进行ausm+格式离散，积分-微分得到模型边界处的无粘通量；

步骤4、打开改良后辐射模型dom，得到模型辐射吸收系数：利用dom模型对辐射传热的积分-微分基本方程离散；得到各点的辐射强度值；

步骤5、用rngk-ε湍流模型进行求解，输出马赫数、温度、压力流场及对流/耦合热流云图。

本发明与现有技术相比，其显著优点是：

(1)本发明的多喷管火箭流场及对流/辐射耦合换热的仿真方法，有效解决了多喷管火箭整体流场区域大、网格规模大、难以计算的问题，同时解决了多喷管燃气羽流相互作用导致难以计算的问题；

(2)本发明的多喷管火箭流场及对流/辐射耦合换热的仿真方法，采用的ausm+离散格式能够准确处理粘性流场中的剪切流；

(3)本发明的多喷管火箭流场及对流/辐射耦合换热的仿真方法，对dom辐射模型进行改良，减少了多喷管火箭辐射换热计算时间；

(4)本发明的多喷管火箭流场及对流/辐射耦合换热的仿真方法，采用的rngk-ε模型是在标准k-ε方程的基础上进行了改进，考虑了湍流漩涡，使得漩涡计算精度更高，还能高效处理近壁区域，进而对低雷诺数流粘性方程进行求解。

附图说明

图1为关于多喷管火箭流场及对流/辐射耦合换热的仿真方法结构流程图。

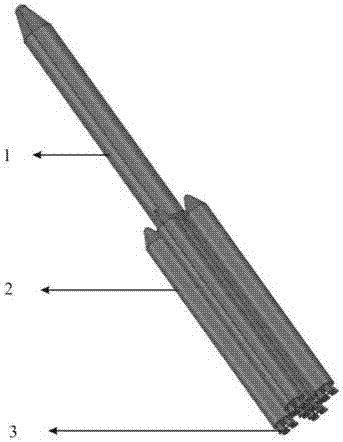
图2为某四助推多喷管火箭三维模型图。

图3为某四助推多喷管火箭多重分块结构化网格图。

图4是某四助推多喷管火箭马赫数场云图。

图5是某四助推多喷管火箭温度场云图。

图6是某四助推多喷管火箭压强场云图。

图7是某四助推多喷管火箭底部对流/辐射热流耦合云图。

具体实施方式

为了说明本发明的技术方案及技术目的，下面结合附图及具体实施例对本发明做进一步的介绍。

结合图1，本发明的一种关于多喷管火箭流场及对流/辐射耦合换热的仿真方法，包括以下步骤：

步骤1、建立多喷管火箭三维模型；

结合图2，三维模型包括芯级段1、多个助推器2以及喷管3；三维模型参数要与实际工程保持一致，模型参数包括模型芯级段1高度、半径；助推器2高度、半径；喷管3内径、外径、喷管3喉部半径参数，与实际工程多喷管火箭进行1：1等比建模。

步骤2、利用多重分块结构化网格方法对三维模型进行网格划分；

结合图3，首先对多喷管火箭三维模型进行分块处理，将总体计算域分为三个子域：芯级段1及环绕芯级段1的外域；助推器2以及喷管3区域；喷管3下方燃气羽流区域。

然后对激波强间断区域进行结构化网格加密处理，保证网格的正交性和光顺性，对其它计算区域网格作由密到疏过渡处理。

步骤3、建立多喷管火箭羽流流场以及对流换热的数学模型：对n-s多组分方程进行ausm+格式离散，积分-微分得到模型边界处的无粘通量；

由于多喷管火箭多采用气体燃料，燃气成分包含h2o，co2，co，h2，n2等，因此采用燃气和空气多组份流动模型。

3.1、在建立多喷管火箭羽流流场以及对流换热的数学模型之前，先对燃气射流作以下基本假设：(1)燃气射流满足连续介质；(2)燃气射流为可压缩纯气相介质；(3)燃气射流内部无化学反应发生；(4)采用燃气和空气多组份混合流动模型，多种组份均满足理想气体状态方程。

3.2、上述假设保证燃气为牛顿粘性流体，故建立燃气多组份输运方程为

其中，yi为火箭燃气组份i的质量分数，为火箭燃气组份扩散通量，ri为火箭燃气组份i经过化学反应的净生成率，si为由自定义源项的火箭燃气弥散相所引起的生成率，t为多喷管火箭飞行时间，ρ为火箭燃气的流体密度，n为火箭燃气组份的数量。

其中，式(1)中的组份扩散通量为

式(2)中，di,m为混合介质中组份i的扩散系数，为燃气流微元体的散度。

3.3、上述假设燃气为可压缩气体，在直角坐标系下，建立可压缩纳维斯托克方程(n-s方程)的守恒形式为：

其中，v为火箭飞行的速度矢量，q为火箭燃气燃烧热量，s为多喷管火箭的广义源项，为直角坐标系x、y、z方向上的方向向量，e、f和g为x，y，z方向上的火箭燃气流通量矢量，ev、fv和gv为x，y，z方向上的火箭燃气粘性通量矢量。

3.4、对n-s方程进行ausm+格式离散，求解模型边界处的无粘通量：

n-s方程直接求解过程繁琐，耗费大量计算时间，特别是多组份输运情况给计算加大了难度，ausm+格式具有较强的分辨激波、滑流等物理间断的能力，而且具有良好的保正定性、计算高速流时不会产生红玉现象、容易向其它双曲型系统扩展、计算中能较好处理激波低速传播的情况、计算效率高等特点。这就使得它不仅能够以高分辨率求解无粘流场中的激波，也能够准确处理粘性流场中的剪切流等问题。

3.4.1、利用ausm+格式基本形式，离散化得到无粘项通量：

(a)利用ausm+格式将无粘项通量分解为物理属性不同的火箭燃气流对流项fc和火箭燃气流压力项fp：

(b)对式(4)中的火箭燃气流对流项fc和火箭燃气流压力项fp进行简化

fc＝m·a·q(5)

q＝(ρ,ρμ,ρν,ρh)^t(6)

fp＝(0,p,p,0)^t(7)

式(5)、(6)、(7)中，m为火箭飞行的马赫数，a为当地声速，q为火箭燃气流相应的流动参数，μ、υ表示燃气速度矢量在x、y方向的分量，h＝e+p/ρ表示火箭燃气燃烧焓，p为火箭燃气的压力项，e为数学常数。

(c)因此，模型边界处的燃气流对流通量和气流压力通量可表示为：

因此，要得到完整的ausm+格式离散化n-s多组分方程，必须要得到边界火箭燃气流对应的流动参数q1/2、边界处马赫数参数m1/2、边界处压力参数p1/2以及边界处声速a1/2。

3.4.2、求解边界火箭燃气流对应的流动参数q1/2：

边界处流动参数q1/2可以根据左、右两侧边界控制体参数ql、qr，结合网格界面的速度方向来确定：

式中，m1/2表示边界处马赫数。

3.4.3、求解边界处马赫数参数m1/2和边界处压力参数p1/2：

(a)在计算边界处对流速度时，考虑到边界处马赫数m1/2受左右特征波影响的物理特性，引入马赫数分裂函数：

(b)边界处马赫数m1/2定义为：

式(12)中的与分别为左、右两侧控制体马赫数的增加量和减小量；

(c)于是对流通量项可表示为：

(d)引入压力分裂函数p^±：

(e)于是边界处压力可表示为：

式(15)中pl⁺与pr^-表示左、右两侧控制体压力分裂函数的增加量和减小量，pl与pr表示左右两侧控制体压力参数。

3.4.4、求解边界处声速a1/2：

(a)定义边界两侧的马赫数为：

ml,r＝ul,r/a1/2(16)

式(16)中，ul，r为火箭向边界两侧实际飞行速度矢量，计算声速时使用的速度为边界法线方向的分量(即速度向量在法线方向的投影，也即穿越边界的速度)，即：

式(17)中，表示燃气向边界两侧实际运动速度，表示边界的运动速度，n表示速度向量在法线方向的单位向量。

(b)定义边界处声速a1/2：

式中，为边界两侧燃气流微元体的声速。

3.5、利用ausm+格式完整表达式，求解模型边界处的无粘通量：

结合式(4)-(19)，ausm+格式下的边界处的无粘通量f1/2可重写为：

ausm+格式兼有roe格式和vanleer格式的优点，而且克服了二者的缺点。它具有数值耗散小、间断分辨率高、无需熵修正、计算量小等优点。

步骤4、打开改良后辐射模型dom，得到模型辐射吸收系数：利用dom模型对辐射传热的积分-微分基本方程离散；

在常用的辐射模型中，dom辐射模型的能量不平衡率最小，其次是s2s模型和rosseland的辐射模型，p-1辐射模型虽然能量不平衡率较小，计算量较低，但是精度达不到航空火箭要求。dom辐射模型在计算气体辐射热流方面，计算精度高，计算时间略长，但对原有辐射模型进行优化求解可降低计算成本。

4.1、定义辐射传热的积分-微分基本方程：

对发动机燃气进行组分分析，获得火箭燃气组分的摩尔百分比，并测量得到多喷管火箭环境温度、飞行速度、环境压强、喷管内部压强、喷管壁面及箭体底部初始温度以及喷管内部温度，将上述多喷管火箭参数代入辐射传热的积分-微分基本方程

式中：s为方向矢量；为燃气扩散项，i为燃气介质辐射强度；ib为黑体的辐射强度；ka，ks分别为多喷管火箭喷流尾流介质的吸收系数与散射系数；为燃气相函数，表示内向散射的空间分布特性。

4.2、用dom模型离散辐射传热基本方程：

用dom模型将辐射传热离散为m个离散的方向，每一个方向对应一定的立体角，在此角度内，辐射强度为定值。于是辐射传热方程变为如下的形式

式中：μ，η，ξ分别表示相对于几何直角坐标系中的方向余弦，km′表示为积分集的权值，m′表示为离散方向的异性，im表示边界上出去的辐射强度，im′表示边界上进入的辐射强度，hm′，m为线性各向散射项函数。

联立式(20)、(21)求解，即可得到各点的辐射强度值。

步骤5、用rngk-ε湍流模型进行求解，输出马赫数、温度、压力流场及对流/耦合热流云图。

5.1、建立rngk-ε湍流模型

建立湍流模型是为了使雷诺应力封闭，目前经常使用的湍流模型有零方程模型、一方程模型、标准k-ε两方程模型、rngk-ε模型和realizablek-ε模型等，由于两方程模型计算精度较高，计算时间少，因此越来越被广泛地应用于工程计算中，通常用湍动能k和耗散率ε来描述湍流特征尺度。rngk-ε模型在标准k-ε方程的基础上进行了改进，并考虑了湍流漩涡，漩涡计算精度更高，还能高效处理近壁区域，进而对低雷诺数流粘性方程进行求解。

湍流模型采用rngk-ε模型，表示为

其中，k为火箭燃气的湍动能，ε为火箭燃气的湍动耗散率，μi为燃气组份i的湍动粘度，μeff为燃气扩散系数，xi与xj为方程对流项与扩散项的变量，c1ε、c2ε、c3ε为经验常数，gk是由火箭燃气流速度梯度而产生的湍流动能，gb是由火箭燃气浮力而产生的湍流动能。ym表示在可压缩湍流中火箭燃气从脉动耗散到完全耗散的贡献。αk和αε是k方程和ε方程的普朗特数。sk和sε是用户自定义的源项。

5.2、输出云图

将建立好的rngk-ε湍流模型输入仿真软件中求解，计算后可得到仿真结果，仿真结果包括马赫数、温度、压力流场及对流/耦合热流云图。

实施例

一种关于多喷管火箭流场及对流/辐射耦合换热的仿真方法，按上述具体实施方式中步骤，包括以下步骤：

步骤1、建立多喷管火箭三维模型；

结合图2，三维模型包括芯级段1、四个助推器2以及二十个喷管3，与实际工程多喷管火箭进行1：1等比建模。

步骤2、利用多重分块结构化网格方法对三维模型进行网格划分；

结合图3，对几何模型进行多重分块结构化网格处理，对某四助推二十喷管火箭划分网格，最后网格总数在1221万左右。

步骤3、建立多喷管火箭羽流流场以及对流换热的数学模型：对n-s多组分方程进行ausm+格式离散，积分-微分得到模型边界处的无粘通量；

燃气组份包括h2o、co2、co、h2、n2，摩尔质量百分比分别为35％、26％、25％、9％、5％，代入多组分方程求解。

步骤4、打开改良后辐射模型dom，得到模型辐射吸收系数：利用dom模型对辐射传热的积分-微分基本方程离散；

飞行高度：10km环境温度：200k飞行速度：1.2ma环境压强：25600pa

喷管内部压强：1.8*10⁶pa喷管壁面及箭体底部初始温度：400k

喷管内部温度：3800k辐射吸收系数：0.3

输入求解各点辐射强度。

步骤5、用rngk-ε湍流模型进行求解，输出马赫数、温度、压力流场及对流/耦合热流云图。

用基于rans理论分析的rngk-ε湍流模型求解计算，所设计的多喷管火箭羽流流场以及对流/辐射耦合换热的数值仿真方法在利用32个cpu并行计算的情况下耗时两天左右输出马赫数场、温度场、压力场、总热流分布云图，如图4-图7所示，图4显示该多喷管火箭最大马赫数在5左右，图5显示该多喷管火箭温度最高值在喷管口以及激波交汇位置，图6显示该多喷管火箭外部压强峰值在弹头弓形激波区域，图7显示火箭底部热流峰值为46783w/m²，越接近中心位置热流越大，并且呈圆形向外均匀分布，与类似工程试验结果对比显示出本仿真方法具有较高的精度。本发明方法能够在提高计算精度的同时降低计算成本，计算结果能为火箭底部热防护提供指导意义。