一种正断层对冲击地压诱导的数值模拟方法与系统与流程

本发明涉及冲击地压数值模拟领域，特别是一种正断层对冲击地压诱导的数值模拟方法与系统。

背景技术：

断层赋存打断了底板连续性，使断层附近岩体力学性能降低，同时造成断层附近应力变异。实践证明，分析断层附近覆岩运动规律及其应力状态是研究冲击地压的基础，可预测出冲击地压危险程度及其危险区域，从而有效防治冲击地压。

近年来，数值模拟作为常用且行之有效的分析方法解决了诸多煤矿复杂力学问题。目前国内外常用的数值模拟软件有flac、udec、pfc、rfpa、ansys等，而采用的方法主要是有限元法、边界元法、离散元法等。其中，flac3d主要用于模拟地质材料的力学行为，特别是材料达到屈服极限后产生的塑性流动；并可解决地质材料的应变硬化或软化、孔隙介质应力-渗流耦合等问题；且程序内设置界面单元，可模拟断层、节理和摩擦边界的滑动。

因此，为认识并探究断层附近冲击地压的诱发机理，本发明实施例尝试采用flac3d数值模拟方法，建立正断层与上、下盘工作面开采的简化数值模型，以研究宏观大尺度上、下盘工作面向正断层开采时煤体超前支承压力、顶板运移量及其运移速度、断层面应力状态及其滑移量等诱冲因素对冲击地压作用的一般规律，为类似条件工作面前方正断层影响区冲击地压预测与防治提供科学依据。

技术实现要素：

本发明的目的是提供一种正断层对冲击地压诱导的数值模拟方法与系统，旨在解决解决了现有技术中对冲击地压影响规律的研究缺乏精确的数值模型支持的问题，实现对正断层的数值模型的建立，模型精确度高。

为达到上述技术目的，本发明提供了一种正断层对冲击地压诱导的数值模拟方法，包括以下操作：

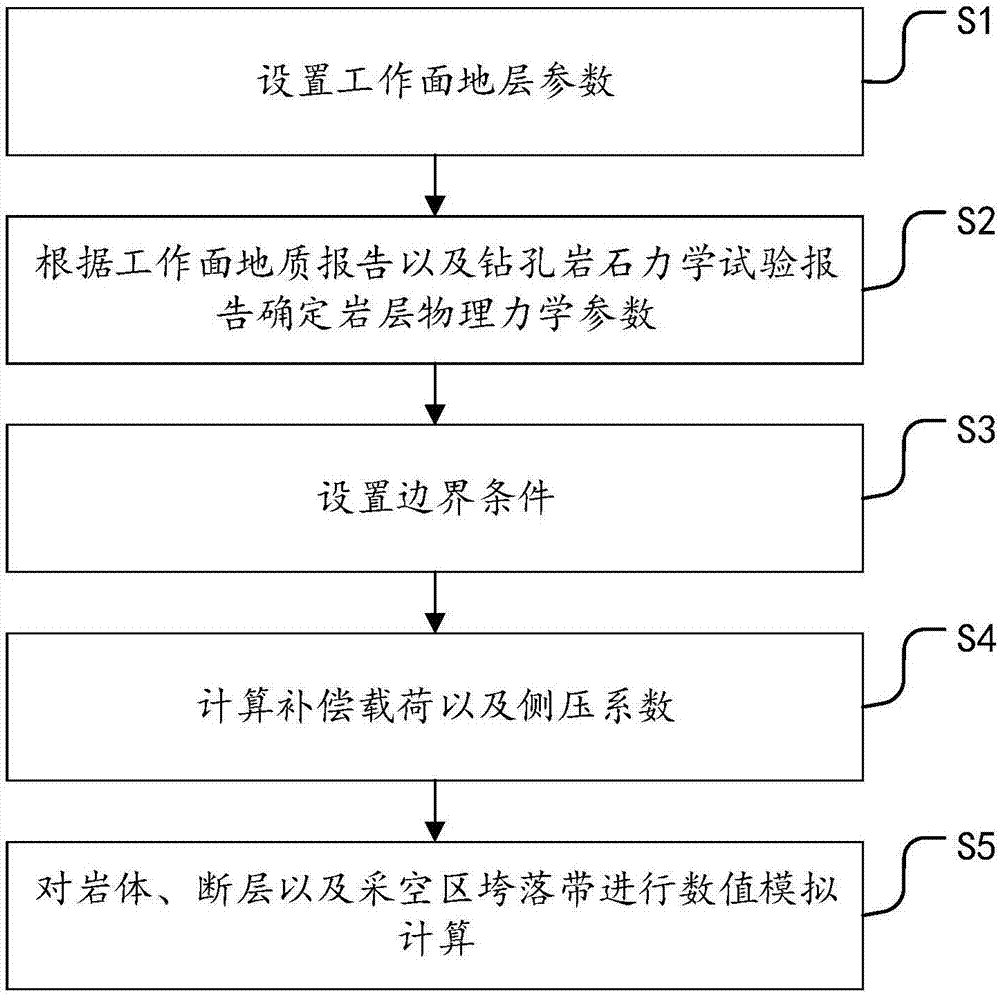
设置工作面地层参数；

根据工作面地质报告以及钻孔岩石力学试验报告确定岩层物理力学参数；

设置边界条件；

计算补偿载荷以及侧压系数；

对岩体、断层以及采空区垮落带进行数值模拟计算。

优选地，所述设置边界条件具体为：

底部边界采用全约束边界条件，左右两侧边界采用水平方向约束、竖直方向自由的边界条件，顶端采用自由边界条件。

优选地，所述补偿载荷的计算如下：

σv＝γhv

式中，γ为未模拟岩层平均容重；hv为未模拟岩层高度。

优选地，所述侧压系数为两水平主应力的平均值与垂直应力的比值。

优选地，所述岩体的计算采用摩尔-库仑强度准则，断层的计算采用coulomb抗剪强度准则，采空区垮落带采用双屈服模型。

本发明还提供了一种正断层对冲击地压诱导的数值模拟系统，所述系统包括：

参数设置模块，用于设置工作面地层参数；

力学参数确定模块，用于根据工作面地质报告以及钻孔岩石力学试验报告确定岩层物理力学参数；

边界条件设置模块，用于设置边界条件；

载荷及侧压确定模块，用于计算补偿载荷以及侧压系数；

数值计算模块，用于对岩体、断层以及采空区垮落带进行数值模拟计算。

优选地，所述边界条件的选择具体为：

底部边界为全约束边界条件，左右两侧边界为水平方向约束、竖直方向自由的边界条件，顶端为自由边界条件。

优选地，所述补偿载荷的计算如下：

σv＝γhv

式中，γ为未模拟岩层平均容重；hv为未模拟岩层高度。

优选地，所述侧压系数为两水平主应力的平均值与垂直应力的比值。

优选地，所述岩体的计算采用摩尔-库仑强度准则，断层的计算采用coulomb抗剪强度准则，采空区垮落带采用双屈服模型。

发明内容中提供的效果仅仅是实施例的效果，而不是发明所有的全部效果，上述技术方案中的一个技术方案具有如下优点或有益效果：

与现有技术相比，本发明通过采用flac3d数值模拟方法，建立了正断层与上、下盘工作面开采的简化数值模型，通过对工作面的参数的数值采集，确定岩层物理力学参数，并对工作面各个边界采用不同的边界条件，并计算补偿载荷以及侧压系数，分别对岩体、断层以及采空区进行数值计算，以此来分析正断层对冲击地压的影响规律，解决了现有技术中对冲击地压影响规律的研究缺乏精确的数值模型支持的问题，实现对正断层的数值模型的建立，根据岩层的既定力学参数进行建模，模型精确度高，为类似条件工作面前方正断层影响区冲击地压预测与防治提供科学依据。

附图说明

图1为本发明实施例中所提供的一种正断层对冲击地压诱导的数值模拟方法流程图；

图2为本发明实施例中所提供的一种正断层flac3d三维数值计算模型示意图；

图3为本发明实施例中所提供的一种正断层对冲击地压诱导的数值模拟系统结构框图。

具体实施方式

为了能清楚说明本方案的技术特点，下面通过具体实施方式，并结合其附图，对本发明进行详细阐述。下文的公开提供了许多不同的实施例或例子用来实现本发明的不同结构。为了简化本发明的公开，下文中对特定例子的部件和设置进行描述。此外，本发明可以在不同例子中重复参考数字和/或字母。这种重复是为了简化和清楚的目的，其本身不指示所讨论各种实施例和/或设置之间的关系。应当注意，在附图中所图示的部件不一定按比例绘制。本发明省略了对公知组件和处理技术及工艺的描述以避免不必要地限制本发明。

下面结合附图对本发明实施例所提供的一种正断层对冲击地压诱导的数值模拟方法与系统进行详细说明。

如图1所示，本发明实施例公开了一种正断层对冲击地压诱导的数值模拟方法，包括以下步骤：

s1、设置工作面地层参数；

s2、根据工作面地质报告以及钻孔岩石力学试验报告确定岩层物理力学参数；

s3、设置边界条件；

s4、计算补偿载荷以及侧压系数；

s5、对岩体、断层以及采空区垮落带进行数值模拟计算。

本发明实施例以新巨龙煤矿2301n首采工作面地层为参考依据，采用flac3d模拟软件，建立工作面与正断层空间位置关系的数值模型。

工作面开切眼附近13-2s钻孔揭露顶底板岩层主要为砂岩和泥岩，对其厚度进行适当调整；考虑消除边界效应影响，工作面走向两侧各留设150m煤柱，倾向方向两侧各留设125m煤柱，同时为消除底部边界对煤层支承压力的影响，工作面底板厚度留设100m，模拟工作面长度100m，最终确定模型长×宽×高为700m×350m×228m，其中模型顶板厚度120m，模拟煤层开采厚度8m，埋深为700m。

煤岩层被正断层贯穿切割，模型由上盘、断层和下盘三部分组成，断层带采用软弱岩体来模拟，倾角45度，落差4m，破碎带宽度2m，根据相关工作面地质报告以及钻孔岩石力学试验报告，确定模型岩层物理力学参数，如表1所示。

表1

断层破碎带岩体破碎、强度低，选择断层带的物理力学参数如表2。

表2

由于岩体节理摩擦角一般取值21-38度，因此断层摩擦角取其中间值30度，而断层或者节理强度一般很低，因此粘聚力和抗拉强度取值0。

数值模型底部边界采用全约束边界条件，左右两侧边界采用水平方向约束、竖直方向自由的边界条件，顶端采用自由边界条件。模拟工作面埋深700m，模型顶板岩层高120m，上部未模拟岩层自重以均步载荷垂直施加于模型顶端，因此补偿载荷应为：

σv＝γhv＝25.5×580kpa＝14.70mpa

式中，γ为未模拟岩层平均容重，取25.5kn·m-³；hv为未模拟岩层高度，580m。

侧压系数的选择采用两水平主应力的平均值与垂直应力的比值，由下述公式：

λ＝129.6/h+0.5595

计算得到λ＝0.74。

根据霍克和布朗回归公式：

100/h+0.3≤λ≤1500/h+0.5

计算得0.44≤λ≤2.64，λ＝0.74满足上述两个条件，因此侧压系数λ取值0.74是合理的，且水平应力采用梯形均布载荷施加。

数值模型中岩体计算采用摩尔-库仑强度准则，断层计算采用coulomb抗剪强度准则。针对采空区垮落带的数值模拟，建立flac3d垮落碎胀岩体精细数值计算模型，采用双屈服模型进行单轴压缩模拟试验，监测模型垮落带应力-应变关系，与其理论解析解进行对比，采用试错反演法得到高拟合精度的采空区模型力学参数，双屈服模型能够准确呈现出垮落带岩体压实过程中的力学特性。力学参数选取如表3所示。

表3

数值计算模型如图2所示。

由于冲击地压诱发与应力场及其动态演化存在密切联系。一般而言，高支承压力集中区易积聚弹性应变能，冲击危险越大。因此，根据所建数值计算模型，对工作面煤体超前支承压力进行模拟，分析并对比了工作面距断层不同距离时断层对煤体超前支承压力的影响，并在开采盘煤层中间(y＝175m)设置了应力监测线，得到工作面煤体超前支承压力演化规律。

本发明实施例通过采用flac3d数值模拟方法，建立了正断层与上、下盘工作面开采的简化数值模型，通过对工作面的参数的数值采集，确定岩层物理力学参数，并对工作面各个边界采用不同的边界条件，并计算补偿载荷以及侧压系数，分别对岩体、断层以及采空区进行数值计算，以此来分析正断层对冲击地压的影响规律，解决了现有技术中对冲击地压影响规律的研究缺乏精确的数值模型支持的问题，实现对正断层的数值模型的建立，根据岩层的既定力学参数进行建模，模型精确度高，为类似条件工作面前方正断层影响区冲击地压预测与防治提供科学依据。

如图3所示，本发明实施例还公开了一种正断层对冲击地压诱导的数值模拟系统，所述系统包括：

参数设置模块，用于设置工作面地层参数；

力学参数确定模块，用于根据工作面地质报告以及钻孔岩石力学试验报告确定岩层物理力学参数；

边界条件设置模块，用于设置边界条件；

载荷及侧压确定模块，用于计算补偿载荷以及侧压系数；

数值计算模块，用于对岩体、断层以及采空区垮落带进行数值模拟计算。

所述边界条件的选择具体为：

底部边界为全约束边界条件，左右两侧边界为水平方向约束、竖直方向自由的边界条件，顶端为自由边界条件。

所述补偿载荷的计算如下：

σv＝γhv

式中，γ为未模拟岩层平均容重；hv为未模拟岩层高度。

所述侧压系数为两水平主应力的平均值与垂直应力的比值。

所述岩体的计算采用摩尔-库仑强度准则，断层的计算采用coulomb抗剪强度准则，采空区垮落带采用双屈服模型。

以上所述仅为本发明的较佳实施例而已，并不用以限制本发明，凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明的保护范围之内。