基于双目视觉的模型位姿计算方法与流程

本发明属于风洞试验技术测控领域，具体涉及一种基于双目视觉的模型位姿计算方法。

背景技术：

投放试验是风洞中的一种常见的特种试验，根据相似准则原理模拟飞行器外挂物投放后的飞行轨迹，是评估外挂物分离安全可靠性的一种试验手段。该试验一般通过投放机构来控制模型投放的初始速度、加速度，同时用高速摄影设备来采集投放过程中模型位姿图像序列。

完成风洞投放试验主要包含两项主要内容，一是利用两台高帧率、高分辨率的cmos电路高速摄影相机作为视频采集设备，同时采用大功率直流led照明设备作为试验光源，采集到分辨率高、对比度强的图像序列作为原始计算依据，二是采用计算机双目视觉技术和数字图像处理方法来从二维图像中提取模型表面的二维特征用来还原模型的三维空间信息，最终利用这些空间信息和先验条件来计算在不同时刻下的空间位移和姿态角，计算模型在整个投放过程中的下落轨迹。

需要根据视频序列来计算出所投放的外挂物模型的位移和姿态角序列。这个过程中涉及到如何准确地获得模型表面的标志点在图像中的二维坐标位置，如何根据一组同态的二维空间信息还原得到模型的三维空间信息，如何根据模型表面的标志点三维空间信息计算获得模型的位移变化量和姿态角变化量，都属于技术难点。

技术实现要素：

基于以上不足之处，本发明提供一种基于双目视觉的模型位姿计算方法，在不依赖模型几何外观的前提下，将数字图像处理算法和计算机双目测量技术应用到风洞试验，满足对风洞投放试验需要，测量飞机吊舱、副油箱等投放模型在制定风洞试验条件下的下落轨迹测量。

本发明所采用的技术如下：一种基于双目视觉的模型位姿计算方法，步骤如下：

步骤1、根据模型的三维数模，以模型质心为几何中心构建模型的体轴坐标系，在三个轴上选取三个到质心位置pc相等的三个点分别为px、py和pz，之后在模型表面布置n个标志点并将这些标志点编号并得到每个标志点到上述四个控制点pc、px、py和pz的距离；

步骤2、在固定好两台高速相机位置之后，采用张氏标定法计算双目参数和镜头畸变参数，并采用棋盘标定版作为计算参照获得相机坐标系和风洞坐标系之间的几何关系；

步骤3、采用模板匹配结合特征矩，提取出模型表面的标志点在图像中的成像质心位置，将两组图像中的标志点进行一一对应；

步骤4、利用畸变参数对标志点在左右图像中的成像位置进行校正之后，根据双目测量方法，连同双目相机参数一同带入三角测量关系式，得出这些标志点在相机坐标系下的空间位置；

步骤5、利用步骤1中获得的标志点到模型轴线上四个控制点px、py和pz的距离，采用极小二乘的方法计算出模型的质心和模型体轴三个控制点在相机坐标系下的位置，此基础上建立模型的体轴坐标系；

步骤6、计算当前时刻模型质心位置到初始状态下模型的质心位置的向量和当前模型体轴系和初始状态下模型体轴系的转角，即求解出位移和姿态角在相机坐标系下的变化，再根据相机坐标系和风洞坐标系的几何关系，将计算结果投影到风轴系，获得风轴系下模型的位姿变化。

本发明的特点及有益效果：

1.本发明不受到模型几何外形约束，并且实施方便；本方法不依赖模型的几何外形特征，采用的是从计算模型质心位置和模拟体轴系的方法计算模型的试验轨迹；

2.为了捕获模型在亚音速工况下的模型运动过程，本文采用了lucas-kanad光流法检测出模型表面的标志点，既克服试验段内存在着漫反射、散射等干扰，又能够准确地在图像中识别出模型表面标志点位置；

3.在建立模型体轴坐标系计算过程中，采用了最小frobenius范数方法对计算出的体轴系优化；

4.本计算方法可以在相机深范围在1000mm左右时，达到位移测量精度优于2mm；

5.本计算方法易于扩展，计算执行效率高。

附图说明

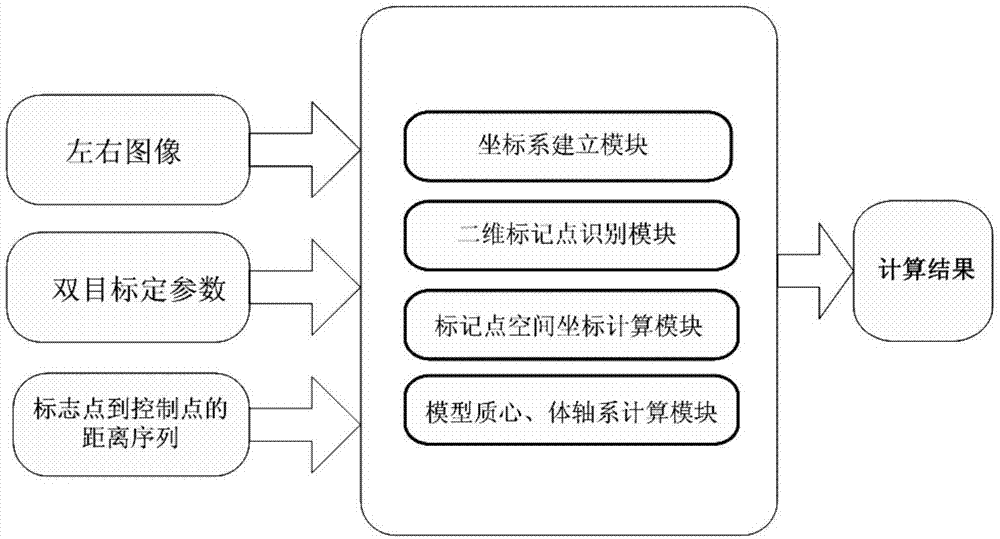
图1是本发明的总体结构框架图；

图2是模型表面标志点提取和标记点三维空间计算流程图；

图3为模型的轴向位移变化曲线图；

图4为模型法向位移变化曲线图；

图5为模型俯仰角变化曲线图。

具体实施方式

根据说明书附图举例对本发明做进一步说明：

实施例1

本方法是将数字图像处理算法和计算机双目视觉技术结合应用于风洞投放试验，测量模型位移和姿态角变化的处理方法。其中根据求解模型质心位置变化量的方法计算位移变化，根据求解模型体轴系的方法，比较不同时刻模型体轴系的变化计算姿态角变化。因此，该方法是采用计算机双目视觉技术和数字图像处理方法来从二维图像中提取模型表面的二维特征用来还原模型的三维空间信息，最终利用这些空间信息和先验条件来计算在不同时刻下的空间位移和姿态角的处理过程。

如图1所示，一种基于双目视觉的模型位姿计算方法，主要包括模型表面标志点布置和空间坐标系建立过程、标志点图像位置检测和空间坐标计算和模型质心位置计算和位移、姿态角求解过程。

步骤1、模型表面标志点布置和空间坐标系建立过程

根据模型的数模，以模型质心位置为几何中心构建模型的体轴坐标系，在三个轴上分别选取三个到质心位置pc相等的三个点分别为px、py和pz。在模型指定位置上布置n个标志点并将这些标志点编号并得到每个标志点到上述四个控制点的距离。

建立相机世界坐标系和风洞坐标系之间的关系是必要过程。该过程首先是采用张正友标定方法确定左右两台高速摄影相机的空间几何关系作为外参、相机的焦距、主点作为内参和镜头畸变参数。同时，根据数目为n(n＞4)个非共线的特征点在左右图像中的一一对应关系，计算两个图像之间的投影矩阵homo。

为了建立风洞坐标系和相机坐标系之间的关系，首先要在与试验段平行的方向上的一个平面上布置n个网格点，使得这些网格点竖直和水平方向上呈正交关系。之后计算这n个标志点位置在相机坐标系下的坐标，根据这些点的空间位置拟合一个平面，并求解出一个该平面正交的单位向量。这样，相机坐标系表示为(xyz)，则风洞坐标系在相机坐标系下可以表示为三个相互正交的单位向量(uvw)，其中u＝(uxuyuz)、v＝(vxvyvz)和w＝(wxwywz)。

步骤2、标志点图像位置检测和空间坐标计算过程

在同一时刻，首先要从这两张图像中提取出标志点在分别在左右图像中的位置imgpointsleft和imgpointsright，之后根据投影矩阵homo计算出两组标志点的一一对应关系，这样就得到两组一一对应的模型表面标志点位置坐标序列：imgpointsleft’和imgpointsright’。这样就可以将之前获得的双目相机标定参数和镜头畸变参数，将消除畸变影响后的两组图像坐标位置带入三角测量关系，得出这些模型表面的标志点在相机坐标系下的空间位置。之后，再根据这些标志点距离模型质心位置的理论距离，求解该时刻模型质心位置。这个过程的流程如图2所示。

步骤3、模型质心位置计算和位移、姿态角求解过程

已知在t时刻计算得到的n个已知模型标志点的空间位置，根据这些点到模型质心的理论距离为{ldmi}，求解模型实际质心即为求取这样一个空间点，使得该点到该组标志点的距离为{ldsi}，满足这两组距离的差的平方和最小：根据非线性极小二乘拟合的方法，将上式作为目标函数，将该组模型标志点到质心的理论距离{ldmi}作为输入，计算得出模型在此时的质心位置。这样对比模型初始状态下的质心位置即可获得此刻模型的位移变化向量，再将该向量投影到风洞坐标系在相机坐标下的三个正交向量(uvw)即可得出模型在风轴系下的变化。类似求解质心过程，同样可以获得模型体轴上三个控制点(pxpypz)的位置，这样就可以建立此时模型的体轴坐标系。对比模型初始状态的体轴系，即可获得该时刻模型姿态角变化。

实施例2

采用本方法，在fl3风洞进成功地完成了多次投放试验。某模型在0.7马赫数且初始攻角为零的的试验轨迹如下:

如图3所示，在爆炸螺栓断裂的10毫秒之内,模型在轴向上的质心并没有发生变化。如图4所示，模型从爆炸螺栓断裂起在气动力和重力的共同作用下开始抛物线运动。如图5所示，从爆炸螺栓断裂起，模型开始翻滚。且这三个方向上的位移/角度变化，均是在风轴系下的试验结果。由于模型在实际运动过程中，侧向几乎没有位移变化且没有发生偏航角和滚转角的变化，这与仿真计算结果基本吻合。

数据的小幅波动与模型加工精度有关，与物理现象无关。下表中给出cfd仿真计算和真实试验的对比结果，从中可以看出试验获得的测量结果与仿真计算结果基本吻合。

表1cfd仿真计算和真实试验的对比结果表